Storyboard

>Modelo

ID:(1628, 0)

Ecuación

>Top, >Modelo

Existen dos tipos de proceso que reducen la energía de los vórtices hasta que pasan a ser fluctuaciones térmicas. Por un lado esta la difusión del momento o viscosidad mientras que por el otro lado esta la flotación.

Por ello con se tiene que

$ \displaystyle\frac{ \epsilon }{ \tau } = \displaystyle\frac{ \epsilon_{\eta} }{ \tau } + \displaystyle\frac{ \epsilon_{ \rho } }{ \tau } $

Condiciones

Variables

$\epsilon_{\rho}$

Energía disipada por flotación

$J$

$\epsilon_{\eta}$

Energía disipada por viscosidad

$J$

$\epsilon$

Energía total disipada

$J$

Relación

ID:(12205, 0)

Ecuación

>Top, >Modelo

Con la velocidad del vórtice y el tamaño de este se puede definir un tiempo característico que permite estimar la perdida de energía tanto por viscosidad como flotación.

Por ello con se tiene que

$ \tau = \displaystyle\frac{ l }{ v_l }$

Condiciones

Variables

$l$

Tamaño del vortice

$m$

$\tau$

Tiempo característico

$s$

$v_l$

Velocidad del vortice

$m/s$

Relación

ID:(12206, 0)

Ecuación

>Top, >Modelo

Como la energía del vórtices es cinética en que por simpleza no consideramos el factor 1/2\\n\\n

$\epsilon =\displaystyle\frac{1}{2}\rho v_l^2\sim \rho v_l^2$

la perdida de energía sera esta energía por el tiempo que con

\\n\\nserá\\n\\n

$\displaystyle\frac{\epsilon}{t} =\rho \displaystyle\frac{v_l^3}{l}$

Por ello con se tiene que

$ \displaystyle\frac{ \epsilon_v }{ \tau } = \displaystyle\frac{ \rho v_l ^3 }{ l }$

Condiciones

Variables

$\rho$

Densidad

$kg/m^3$

$\epsilon_v$

Energía cinética

$J$

$l$

Tamaño del vortice

$m$

$\tau$

Tiempo característico

$s$

$v_l$

Velocidad del vortice

$m/s$

Relación

ID:(12212, 0)

Ecuación

>Top, >Modelo

Como la energía del vórtices es cinética\\n\\n

$\epsilon_{\eta} =\eta\displaystyle\frac{v_l}{l}$

la perdida de energía sera esta energía por el tiempo que con

\\n\\nserá\\n\\n

$\displaystyle\frac{\epsilon_{\eta}}{\tau} =\eta \displaystyle\frac{v_l^2}{l^2}$

Por ello con se tiene que

$ \displaystyle\frac{ \epsilon_{\eta} }{ \tau } = \eta \displaystyle\frac{ v_l ^2 }{ l ^2 }$

Condiciones

Variables

$\epsilon_{\eta}$

Energía disipada por viscosidad

$J$

$l$

Tamaño del vortice

$m$

$\tau$

Tiempo característico

$s$

$v_l$

Velocidad del vortice

$m/s$

$\eta$

Viscosidad del agua oceánica

$Pa s$

Relación

ID:(12207, 0)

Ecuación

>Top, >Modelo

Como la energía potencial de flotación es\\n\\n

$\epsilon_{\rho} =\Delta\rho g \Delta z$

la perdida de energía sera esta energía por el tiempo que con

\\n\\nserá y se asume como tamaño el largo característico l se tiene\\n\\n

$\displaystyle\frac{\epsilon_{\rho}}{\tau} =\Delta\rho g v_l$

Por ello con se tiene que

$ \displaystyle\frac{ \epsilon_{\rho} }{ \tau } = \Delta\rho g v_l $

Condiciones

Variables

$g$

Aceleración gravitacional

$m/s^2$

$\epsilon_{\rho}$

Energía disipada por flotación

$J$

$\tau$

Tiempo característico

$s$

$\Delta\rho$

Variación de la densidad

$kg/m^3$

$v_l$

Velocidad del vortice

$m/s$

Relación

ID:(12208, 0)

Ecuación

>Top, >Modelo

En el caso de que los procesos difusivos son mas relevantes que los de flotación se tiene que\\n\\n

$\epsilon_{\eta}\gg\epsilon_{\rho}$

Dado que la potencia del vórtice es con

y la potencia del efecto de la viscosidad es con energía disipada por viscosidad $J$, tamaño del vortice $m$, tiempo característico $s$, velocidad del vortice $m/s$ y viscosidad del agua oceánica $Pa s$

\\n\\nla existencia del vórtice implica que su energía cinética es mayor que la perdida por lo que con\\n\\n

$\rho\displaystyle\frac{v_l^3}{l}>\eta\displaystyle\frac{v_l^2}{l^2}$

por lo que resulta la exigencia de que con energía disipada por viscosidad $J$, tamaño del vortice $m$, tiempo característico $s$, velocidad del vortice $m/s$ y viscosidad del agua oceánica $Pa s$ se tiene que

$ Re = \displaystyle\frac{ \rho l v_l }{ \eta }$

Condiciones

Variables

$\rho$

Densidad

$kg/m^3$

$Re$

Número de Reynold

$-$

$l$

Tamaño característico

$m$

$v_l$

Velocidad del vortice

$m/s$

$\eta$

Viscosidad del agua oceánica

$Pa s$

Relación

ID:(12209, 0)

Ecuación

>Top, >Modelo

En el caso de que los procesos difusivos son mas relevantes que los de flotación se tiene que\\n\\n

$\epsilon_{\eta}\ll\epsilon_{\rho}$

Dado que la potencia del vórtice es con

y la potencia del efecto de la viscosidad es con aceleración gravitacional $m/s^2$, energía disipada por flotación $J$, tiempo característico $s$, variación de la densidad $kg/m^3$ y velocidad del vortice $m/s$

\\n\\nla existencia del vórtice implica que su energía cinética es mayor que la perdida por lo que con\\n\\n

$\rho\displaystyle\frac{v_l^3}{l}>\Delta\rho g v_l$

por lo que resulta la exigencia de que con aceleración gravitacional $m/s^2$, energía disipada por flotación $J$, tiempo característico $s$, variación de la densidad $kg/m^3$ y velocidad del vortice $m/s$ se tiene que

$ R_i = \displaystyle\frac{\Delta \rho}{\rho}\displaystyle\frac{ g l }{ v_l^2}<1$

Condiciones

Variables

$g$

Aceleración gravitacional

$m/s^2$

$\rho$

Densidad

$kg/m^3$

$R_i$

Numero de Richardson

$-$

$l$

Tamaño del vortice

$m$

$\Delta\rho$

Variación de la densidad

$kg/m^3$

$v_l$

Velocidad del vortice

$m/s$

Relación

ID:(12210, 0)

Imagen

>Top

Como ejemplo se ve en la gráfica a continuación un ejemplo en que se estudia flotación y convección y en que se muestra como ambos casos limites marcan las situaciones del limite de estabilidad:

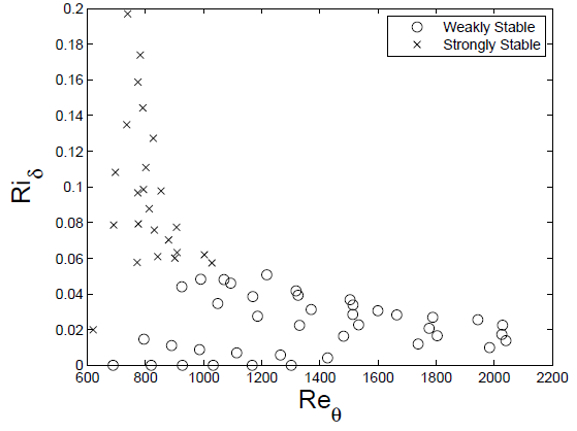
Turbulent Coherent Structures in a Thermally stable Boundary Layer, Owen Williams and Alexander J. Smits, https://www.researchgate.net/publication/228761589_Turbulent_Coherent_Structures_in_a_Thermally_Stable_Boundary_Layer

ID:(12211, 0)

0

Video

Video: Proceso de mezcla en aguas profundas