Trabajo
Storyboard 
El trabajo depende de la forma en que se desarrolla el proceso. Por ejemplo, representa la energía necesaria para aplicar una fuerza específica y desplazar un cuerpo a lo largo de una distancia determinada, o la presión que debe soportar un gas para expandirse en un cierto volumen.
ID:(1470, 0)
Convertidor de trabajo en calor
Imagen 
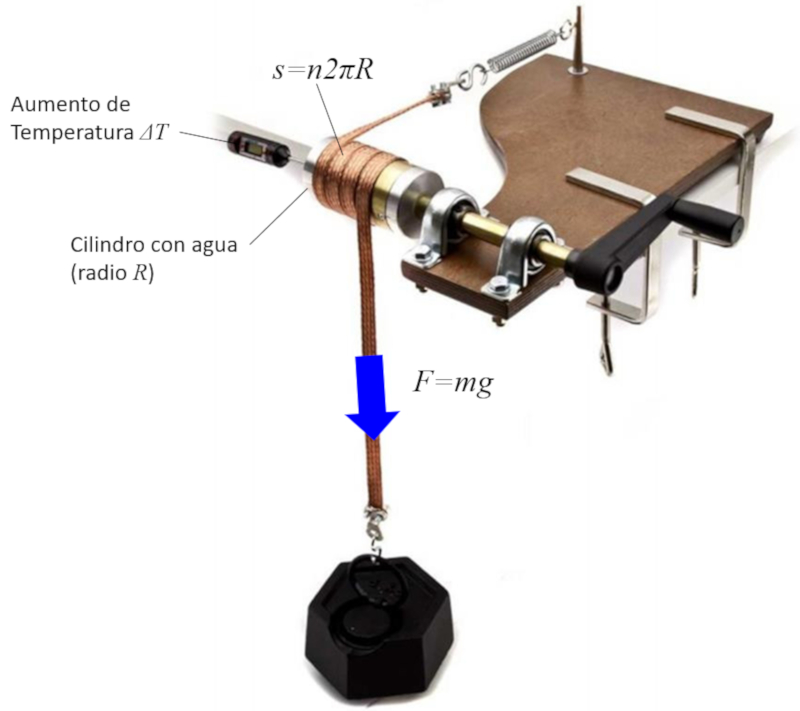
La conversión de trabajo en energía se estudia mediante la generación de calor a través del rozamiento. Para este fin, se coloca una banda metálica alrededor de un cilindro que contiene agua y un termómetro. Al girar la manivela, el rozamiento genera calor, lo que resulta en el calentamiento del agua. Si se mide la fuerza aplicada, el número de vueltas realizadas y el radio del cilindro, es posible estimar la distancia recorrida, lo que permite estimar la energía como el producto de la fuerza por la distancia.
ID:(1884, 0)
Presión y trabajo
Nota 
Consideremos un gas en un cilindro en el cual se puede desplazar un pistón. Si se desplaza el pistón, es posible reducir el volumen comprimiendo el gas. Para realizar esta compresión se requiere de energía, la cual es igual a la fuerza ejercida por el gas multiplicada por la distancia que recorre el pistón. Esta energía también puede representarse en función de la presión, ya que ésta se define por la fuerza y la superficie del pistón.
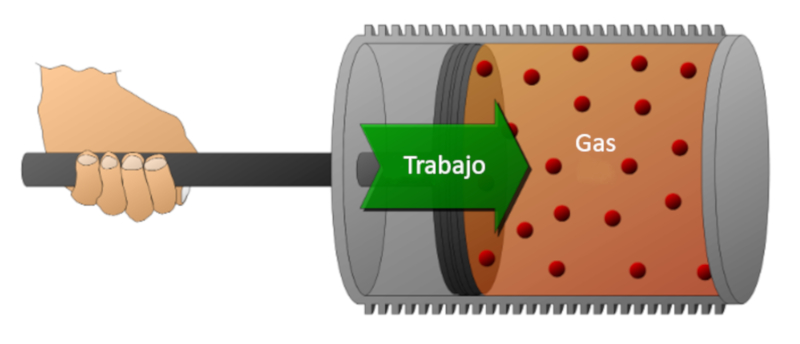
El trabajo puede realizarse sobre el sistema (compresión) o por el sistema sobre el medio externo (expansión).
Dado que la fuerza mecánica ($F$) dividida por la sección ($S$) es igual a la presión ($p$):
| $ p \equiv\displaystyle\frac{ F }{ S }$ |
y la variación del volumen ($\Delta V$) con el camino recorrido ($dx$) es igual a:
| $ \Delta V = S \Delta s $ |
La ecuación para el diferencial inexacto del trabajo ($\delta W$) se puede expresar como:
| $ \Delta W = F \Delta s $ |
Así que puede ser escrita como:
| $ \delta W = p dV $ |
ID:(11126, 0)
Presión y trabajo en un gas
Cita 
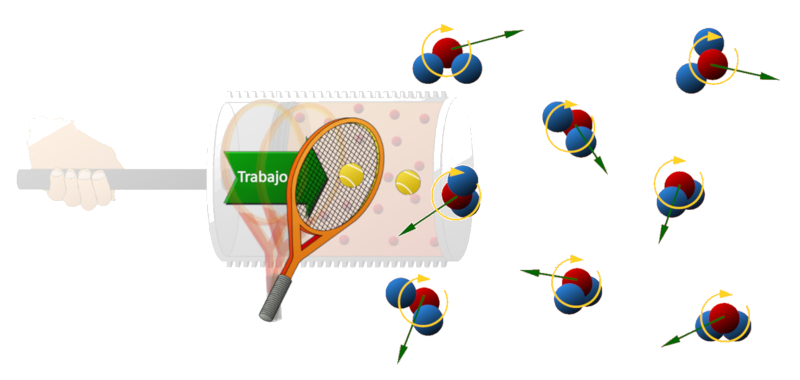
Cuando el émbolo se desplaza dentro del cilindro, funciona como una raqueta de tenis que impulsa las moléculas, otorgándoles energía cinética. Al adquirir mayor velocidad, estas moléculas transfieren un impulso mayor a las paredes, generando así una mayor presión.
ID:(11127, 0)
Presión y trabajo en un liquido/solido
Ejercicio 
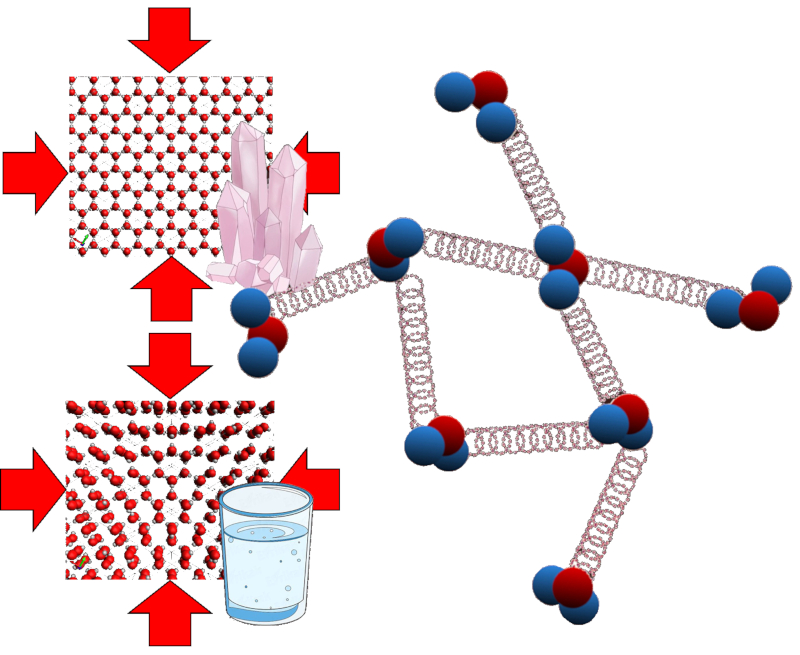
En el caso de un líquido o sólido, una fuerza externa desplaza las partículas del material, lo que afecta la energía potencial de las uniones entre ellas. Se puede imaginar esto como pequeños resortes que se comprimen, lo que aumenta su energía potencial.
ID:(11128, 0)
Trabajo
Descripción 
El trabajo depende de la forma en que se desarrolla el proceso. Por ejemplo, representa la energía necesaria para aplicar una fuerza específica y desplazar un cuerpo a lo largo de una distancia determinada, o la presión que debe soportar un gas para expandirse en un cierto volumen.
Variables
Cálculos
Cálculos
Ecuaciones
(ID 3202)
Dado que la fuerza mecánica ($F$) dividida por la sección ($S$) es igual a la presión ($p$):
| $ p \equiv\displaystyle\frac{ F }{ S }$ |
y la variación del volumen ($\Delta V$) con el camino recorrido ($dx$) es igual a:
| $ \Delta V = S \Delta s $ |
La ecuaci n para el diferencial inexacto del trabajo ($\delta W$) se puede expresar como:
| $ \Delta W = F \Delta s $ |
As que puede ser escrita como:
| $ \delta W = p dV $ |
(ID 3468)
Ejemplos
En termodin mica, el trabajo es la energ a transferida hacia o desde un sistema mediante una fuerza que act a a lo largo de una distancia. Esto puede ocurrir en varias formas, como el trabajo mec nico, donde un gas en un cilindro con un pist n se expande y mueve el pist n, o el trabajo el ctrico, que implica la transferencia de energ a a trav s de fuerzas el ctricas. El concepto de trabajo es crucial para entender los intercambios de energ a y los procesos. Se representa matem ticamente, a menudo involucrando cambios de presi n y volumen en el sistema. Seg n la primera ley de la termodin mica, el cambio en la energ a interna de un sistema es igual al calor a adido al sistema menos el trabajo realizado por el sistema sobre sus alrededores. El trabajo es integral a varios procesos, incluidos los procesos isot rmicos, adiab ticos, isob ricos e isoc ricos, y es esencial en aplicaciones como motores t rmicos y refrigeradores, donde juega un papel clave en la conversi n de calor en trabajo o en el uso de trabajo para transferir calor.
(ID 15247)
La conversi n de trabajo en energ a se estudia mediante la generaci n de calor a trav s del rozamiento. Para este fin, se coloca una banda met lica alrededor de un cilindro que contiene agua y un term metro. Al girar la manivela, el rozamiento genera calor, lo que resulta en el calentamiento del agua. Si se mide la fuerza aplicada, el n mero de vueltas realizadas y el radio del cilindro, es posible estimar la distancia recorrida, lo que permite estimar la energ a como el producto de la fuerza por la distancia.

(ID 1884)
Consideremos un gas en un cilindro en el cual se puede desplazar un pist n. Si se desplaza el pist n, es posible reducir el volumen comprimiendo el gas. Para realizar esta compresi n se requiere de energ a, la cual es igual a la fuerza ejercida por el gas multiplicada por la distancia que recorre el pist n. Esta energ a tambi n puede representarse en funci n de la presi n, ya que sta se define por la fuerza y la superficie del pist n.

El trabajo puede realizarse sobre el sistema (compresi n) o por el sistema sobre el medio externo (expansi n).
Dado que la fuerza mecánica ($F$) dividida por la sección ($S$) es igual a la presión ($p$):
| $ p \equiv\displaystyle\frac{ F }{ S }$ |
y la variación del volumen ($\Delta V$) con el camino recorrido ($dx$) es igual a:
| $ \Delta V = S \Delta s $ |
La ecuaci n para el diferencial inexacto del trabajo ($\delta W$) se puede expresar como:
| $ \Delta W = F \Delta s $ |
As que puede ser escrita como:
| $ \delta W = p dV $ |
(ID 11126)
Cuando el mbolo se desplaza dentro del cilindro, funciona como una raqueta de tenis que impulsa las mol culas, otorg ndoles energ a cin tica. Al adquirir mayor velocidad, estas mol culas transfieren un impulso mayor a las paredes, generando as una mayor presi n.

(ID 11127)
En el caso de un l quido o s lido, una fuerza externa desplaza las part culas del material, lo que afecta la energ a potencial de las uniones entre ellas. Se puede imaginar esto como peque os resortes que se comprimen, lo que aumenta su energ a potencial.

(ID 11128)
(ID 15306)
ID:(1470, 0)
