La pregunta es la probabilidad que existe que se de una combinaci n de eventos A y B.

Para ello se debe entender que interrelaci n, si es que, existe entre ambos eventos y seg n ello poder estimar la probabilidad P(A,B).

(ID 461)

Si los eventos son independientes, el hecho que ocurra uno no afecta a que ocurra el otro.

Un ejemplo serian los eventos

A=\lbrace\mbox{dia asoleado}\rbrace

B=\lbrace\mbox{dia domingo}\rbrace

son independientes ya que el tiempo no se relaciona con el d a de la semana que sea.

(ID 165)

La probabilidad de que ocurran dos eventos independientes del tipo A y B es igual a la multiplicaci n de las probabilidades respectivas P(A) y P(B):

A modo de ejemplo si la probabilidad de que este asoleado es igual a P(asoleado)=0.6 y siendo la probabilidad de que sea domingo es P(domingo)=1/7=0.143 se tiene que la probabilidad de que sea un domingo asoleado es

P(asoleado)P(domingo)=0.6\cdot 0.143=0.086

(ID 3285)

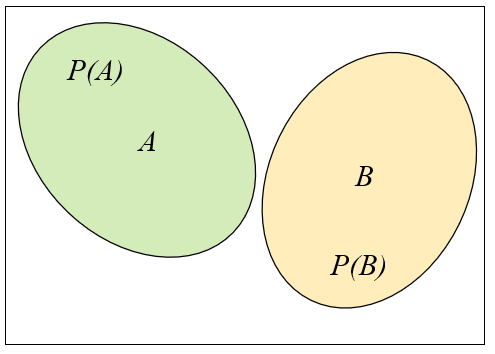
En el caso de que los eventos sean mutuamente excluyentes se tiene que si ocurre A no ocurre B y si ocurre B no ocurre A.

En este caso la probabilidad de que ocurran ambos en forma simultanea es nula. Por ello

La probabilidad de que ocurra A o B corresponde a que cada desenlace que arroja uno o el otro cuenta. Esto corresponde a la uni n de ambos eventos A \cup B y se calcula sumando ambas probabilidades.

(ID 462)

Cuando los eventos A y B son mutuamente excluyente se puede determinar la probabilidad de que ocurra uno o el otro. La probabilidad se calcula como la suma de las probabilidades P(A) que ocurra A y P(B) que ocurra B:

La suma nunca supera la unidad ya que ambos conjuntos no interceptan y en la suma no pueden ser mayor que todos los casos posibles.

(ID 3189)

Representaci n de eventos mutuamente excluyentes

(ID 1666)

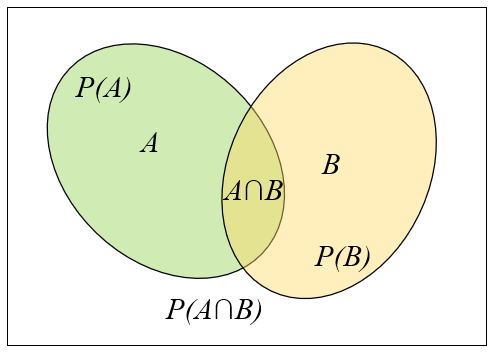
Si los eventos NO son mutuamente excluyentes pueden existir eventos que pertenecen tanto a A como a B.

Esto lleva a que la probabilidad ya no se puede calcular como la suma de las probabilidades ya que la zona de intersecci n se estar a sumando en forma doble.

(ID 166)

Representaci n de eventos Independientes

(ID 1829)

Si los eventos NO son mutuamente excluyentes, los conjuntos pueden tener puntos en com n o sea su intersecci n NO es vac a

Si se desea calcular la probabilidad de que ocurra A o B como la suma se tendr el problema que la zona de la intersecci n se contara en forma doble. Por ello es necesario restar una vez el rea de la intersecci n de modo de tener el total de eventos en forma nica.

(ID 463)

Cuando los eventos A y B NO son mutuamente excluyente la probabilidad se calcula como la suma de las probabilidades P(A) que ocurra A y P(B) que ocurra B, existiendo el problema que el conjunto A \cap B en que pueden coincidir, se estar a sumando dos veces. Por ello la probabilidad es la suma menos la probabilidad de que coincidan:

La suma nunca supera la unidad ya que ambos conjuntos no interceptan y en la suma no pueden ser mayor que todos los casos posibles.

(ID 3286)

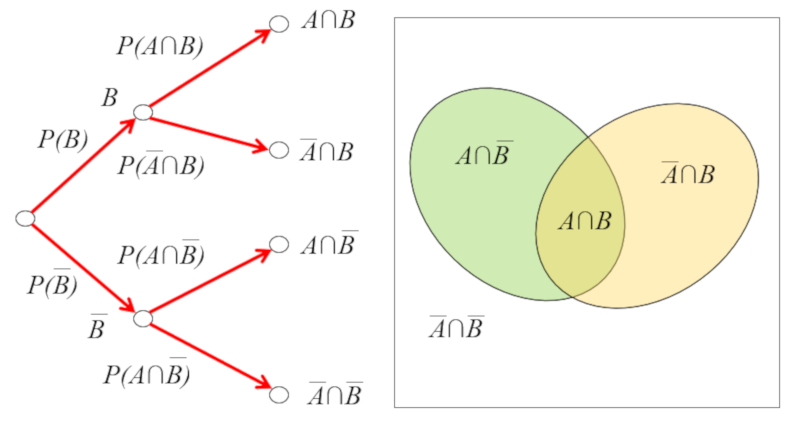
Los eventos pueden ocurrir en secuencia con lo que tiene sentido preguntar la probabilidad de que ocurra B si anteriormente ha ocurrido el evento A.

Para definir dicho tipo de probabilidades se emplea la nomenclatura P(A \mid B).

(ID 496)

Cuando se ha dado el evento B, la probabilidad de que se de A ser

La suma nunca supera la unidad ya que ambos conjuntos no interceptan y en la suma no pueden ser mayor que todos los casos posibles.

(ID 3340)

Representaci n de eventos condicionales

(ID 1841)