Bases de las Probabilidades
Storyboard 
Cada vez que el desenlace de un proceso no es determinístico se puede trabajar con probabilidades para estudiar los desenlaces y hacer a lo menos un pronostico estadístico del resultado del evento.
ID:(429, 0)
El problema
Definición 
Si arrojamos un dado no tenemos forma de poder predecir el número que caerá. Solo sabemos que puede ser un 1, un 2, un 3, un 4, un 5 o un 6.
Por ello debemos considerar situaciones en física en que no exista un resultado único y en que estos ocurren con una cierta frecuencia. Esta frecuencia se asocia a lo que denominamos probabilidad.
En un sistema físico el resultado de un experimento puede ser continuo por lo que el pronostico ni si quiera se puede reducir a indicar pocas alternativas si no que rangos de valores posibles. En este caso no existe una frecuencia de un resultado en particular si no de una gama de valores continua.
En el caso de que el resultado pueda ser cualquier valor dentro de un rango continuo se puede aproximar la discreción mediante la definición de rangos discretos para los que se puede determinar una frecuencia e introducir el concepto de probabilidad.
ID:(455, 0)
Concepto de probabilidad
Imagen 
Si se expresa la probabilidad en forma de porcentajes entonces una probabilidad indica la fracción de las veces para cada 100 eventos que ocurran.
Ejemplo, si la probabilidad es 20% eso significa que ocurrirá en 20 veces cada 100 veces que el evento ocurra.
Aun que se puede expresar la probabilidad como porcentajes se acostumbra a indicarla como una fracción. O sea en el caso de 20% se indica que la probabilidad es de 0.2.
ID:(460, 0)
Notación matemática
Nota 
Lo primero es que debemos definir el evento que queremos analizar. Podemos decir que nos interesa saber la probabilidad de que ocurra un evento
La probabilidad de que el evento
Los casos en que se cumple
ID:(164, 0)
Conjunto y su complemento
Ejercicio 
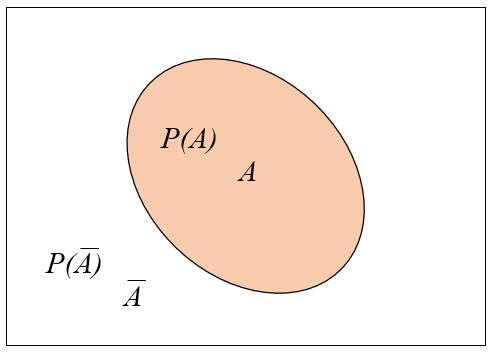
En teoría de conjunto se puede representar los eventos
Las correspondientes probabilidades son aquellas proporciones que corresponden a a que ocurra o no el evento
ID:(1831, 0)
Ejemplo caso discreto
Ecuación 
Si se arroja un dado
Si el número de desenlaces son
| $i$ | $n_i$ | $p_i$ |
| 1 | 15 | 0.15 |
| 2 | 18 | 0.18 |
| 3 | 19 | 0.19 |
| 4 | 22 | 0.22 |
| 5 | 12 | 0.12 |
| 6 | 14 | 0.14 |
ID:(458, 0)
Solución caso discreto
Script 
Si arrojamos en forma repetida el dado veremos que, si el dado es ideal, cada aproximadamente la misma cantidad de veces en cada una de las alternativas posibles.
Por ello, en vez de pronosticar que arrojaremos por ejemplo un 6, podemos decir que en 16.67% de los casos se dará dicho resultado.
En otras palabras en vez de indicar un desenlace podemos indicar la fracción de las veces en que se dará dicho resultado.
ID:(456, 0)
Definición valores medidos
Variable 
En el caso de que el sistema a describir no entregue valores únicos, podemos establecer un conjunto de resultados posibles (eventos discretos o rangos en caso de resultados continuos).
El resultado se describe indicando la fracción de resultados que se da en cada uno de los resultados posibles.
La fracción corresponde a la probabilidad de que una futura medición o cálculo entregue un valor en uno de dichos valores posibles.
ID:(163, 0)
Ejemplo caso continuo
Audio 
En el caso de una variable continua se debe primero segmentar esta en sub-rangos que pueden o no ser de igual largo.
Si estamos estudiando la temperatura media de una sala y esta fluctúa en el día entre
Si el número de veces que se miden las temperaturas en cada rango y estos son (donde el indice
| $i$ | $n_i$ | $p_i$ |
| 18-19 | 30 | 0.30 |
| 20-21 | 54 | 0.54 |
| 22-23 | 16 | 0.16 |
ID:(459, 0)
Solución caso continuo
Video 
Para el caso continuo es necesario que fraccionemos el rango total de la variable a predecir en un número discreto de rangos.
Dichos rangos pueden ser iguales o adecuados al problema que estamos describiendo.
Luego, al igual que en el caso del dado, podemos indicar el porcentaje de veces en que el desenlace del experimento arroja un valor en uno de los rangos.
ID:(457, 0)
Bases de las Probabilidades
Descripción 
Cada vez que el desenlace de un proceso no es determinístico se puede trabajar con probabilidades para estudiar los desenlaces y hacer a lo menos un pronostico estadístico del resultado del evento.
Variables
Cálculos
Cálculos
Ecuaciones
(ID 3188)
Ejemplos
Si arrojamos un dado no tenemos forma de poder predecir el n mero que caer . Solo sabemos que puede ser un 1, un 2, un 3, un 4, un 5 o un 6.
Por ello debemos considerar situaciones en f sica en que no exista un resultado nico y en que estos ocurren con una cierta frecuencia. Esta frecuencia se asocia a lo que denominamos probabilidad.
En un sistema f sico el resultado de un experimento puede ser continuo por lo que el pronostico ni si quiera se puede reducir a indicar pocas alternativas si no que rangos de valores posibles. En este caso no existe una frecuencia de un resultado en particular si no de una gama de valores continua.
En el caso de que el resultado pueda ser cualquier valor dentro de un rango continuo se puede aproximar la discreci n mediante la definici n de rangos discretos para los que se puede determinar una frecuencia e introducir el concepto de probabilidad.
(ID 455)
Si se expresa la probabilidad en forma de porcentajes entonces una probabilidad indica la fracci n de las veces para cada 100 eventos que ocurran.
Ejemplo, si la probabilidad es 20% eso significa que ocurrir en 20 veces cada 100 veces que el evento ocurra.
Aun que se puede expresar la probabilidad como porcentajes se acostumbra a indicarla como una fracci n. O sea en el caso de 20% se indica que la probabilidad es de 0.2.
(ID 460)
Como la probabilidad se define como la fracci n de que ocurra un evento en particular se puede estimar esta simplemente determinando el numero de veces que se da el evento considerado en proporci n a todos los eventos de distintos tipos que se den.
Por ello con se tiene que
| $p_i=\displaystyle\frac{n_i}{N}$ |
\\n\\nComo ejemplo si se tira 20 veces un dado y en 3 ocasiones se obtiene un 6 se puede estimar que la probabilidad de que surja un 6 es del orden de\\n\\n
$p_6=\displaystyle\frac{3}{20}=0.15$
(ID 3284)
Lo primero es que debemos definir el evento que queremos analizar. Podemos decir que nos interesa saber la probabilidad de que ocurra un evento
La probabilidad de que el evento
Los casos en que se cumple
(ID 164)
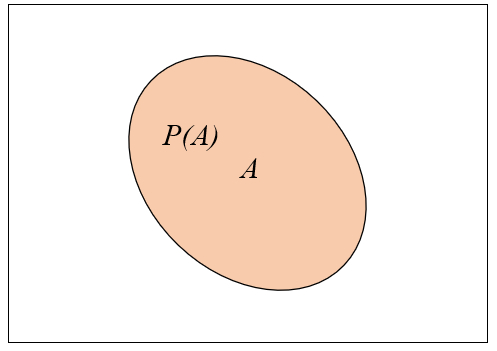
Representaci n de un evento
(ID 1830)
Un evento puede ser parte del conjunto de eventos
Como el evento o es parte de
| $P(A)+P(\bar{A})=1$ |
\\n\\nComo ejemplo, supongamos que la probabilidad de que ocurra un evento del tipo
$P(\bar{A})=1-P(A)=1.0-0.35=0.65$
(ID 3188)
En teor a de conjunto se puede representar los eventos
Las correspondientes probabilidades son aquellas proporciones que corresponden a a que ocurra o no el evento

(ID 1831)
Si se arroja un dado
Si el n mero de desenlaces son
| $i$ | $n_i$ | $p_i$ |
| 1 | 15 | 0.15 |
| 2 | 18 | 0.18 |
| 3 | 19 | 0.19 |
| 4 | 22 | 0.22 |
| 5 | 12 | 0.12 |
| 6 | 14 | 0.14 |
(ID 458)
Si arrojamos en forma repetida el dado veremos que, si el dado es ideal, cada aproximadamente la misma cantidad de veces en cada una de las alternativas posibles.
Por ello, en vez de pronosticar que arrojaremos por ejemplo un 6, podemos decir que en 16.67% de los casos se dar dicho resultado.
En otras palabras en vez de indicar un desenlace podemos indicar la fracci n de las veces en que se dar dicho resultado.
(ID 456)
En el caso de que el sistema a describir no entregue valores nicos, podemos establecer un conjunto de resultados posibles (eventos discretos o rangos en caso de resultados continuos).
El resultado se describe indicando la fracci n de resultados que se da en cada uno de los resultados posibles.
La fracci n corresponde a la probabilidad de que una futura medici n o c lculo entregue un valor en uno de dichos valores posibles.
(ID 163)
En el caso de una variable continua se debe primero segmentar esta en sub-rangos que pueden o no ser de igual largo.
Si estamos estudiando la temperatura media de una sala y esta fluct a en el d a entre
Si el n mero de veces que se miden las temperaturas en cada rango y estos son (donde el indice
| $i$ | $n_i$ | $p_i$ |
| 18-19 | 30 | 0.30 |
| 20-21 | 54 | 0.54 |
| 22-23 | 16 | 0.16 |
(ID 459)
Para el caso continuo es necesario que fraccionemos el rango total de la variable a predecir en un n mero discreto de rangos.
Dichos rangos pueden ser iguales o adecuados al problema que estamos describiendo.
Luego, al igual que en el caso del dado, podemos indicar el porcentaje de veces en que el desenlace del experimento arroja un valor en uno de los rangos.
(ID 457)
ID:(429, 0)
