Rotationskinetische Energie und Trägheitsmomente
Storyboard 
Die kinetische Rotationsenergie ist eine Funktion der Winkelgeschwindigkeit, die durch die Anwendung eines Drehmoments über eine bestimmte Zeit erreicht wird, während ein bestimmter Winkel durchlaufen wird.Daher ist die Rotationskinetik proportional zum Trägheitsmoment des Objekts und dem Quadrat der Winkelgeschwindigkeit.
ID:(1417, 0)
Balken, der sich um eine Achse $\perp$ dreht
Bild 
Ein Balken mit Masse $m$ und Länge $l$, der um sein Zentrum rotiert, das mit dem Schwerpunkt übereinstimmt:
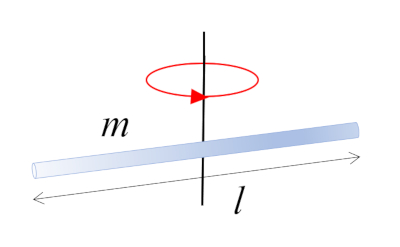
ID:(10962, 0)
Zylinder, der sich um die Achse $\parallel$ dreht
Bild 
Die Drehung eines Zylinders mit Masse $m$ und Radius $r$ um die Achse des Zylinders, wobei sich der Schwerpunkt (CM) in halber Höhe befindet:
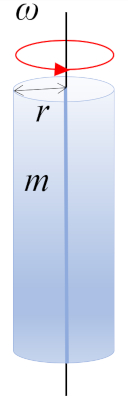
ID:(10964, 0)
Zylinder, der sich um die Achse $\perp$ dreht
Bild 
In dieser Situation rotiert ein Zylinder mit Masse $m$, Radius $r$ und Höhe $h$ um eine Achse, die senkrecht zu seiner eigenen Achse verläuft. Diese Achse verläuft durch den Mittelpunkt der Länge des Zylinders, wo sich der Schwerpunkt (CM) befindet:
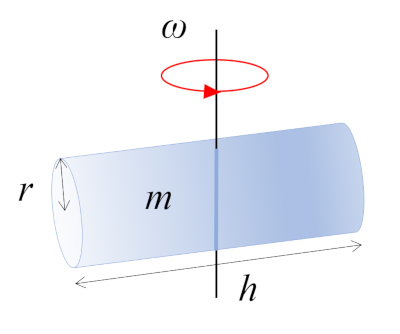
ID:(10965, 0)
Kugel
Bild 
Eine Kugel mit der Masse $m$ und dem Radius $r$ rotiert um ihren Schwerpunkt, der sich im geometrischen Zentrum befindet:
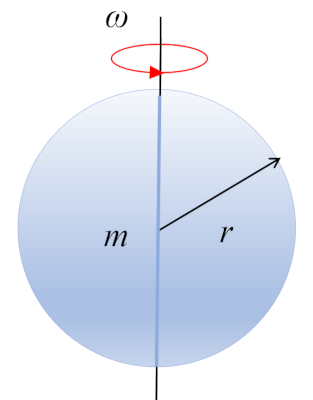
ID:(10490, 0)
Regelmäßiges Parallelepiped-Trägheitsmoment
Bild 
Ein rechtwinkliges Quader mit der Masse $m$ und den Seitenlängen $a$ und $b$, das senkrecht zur Rotationsachse steht, dreht sich um seinen Schwerpunkt, der sich im geometrischen Zentrum des Körpers befindet:
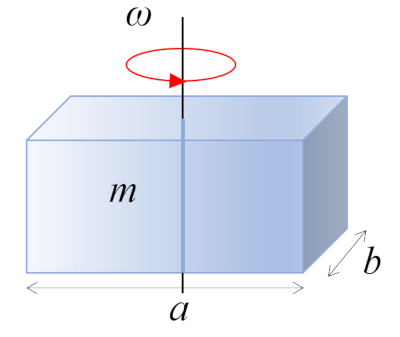
ID:(10973, 0)
Gerade parallelepiped
Bild 
Im Fall eines rechtwinkligen Quaders mit Masse $m$ und Seitenlänge $a$ befindet sich der Schwerpunkt im geometrischen Zentrum:
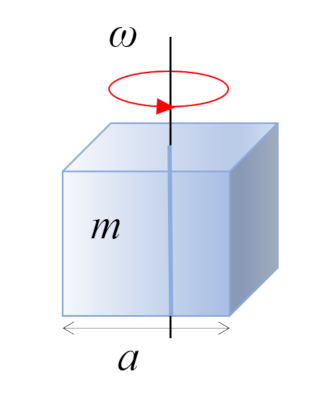
ID:(10963, 0)
Trägheitsmoment
Beschreibung 
In der Rotationsdynamik erfüllt das Trägheitsmoment die gleiche Rolle wie die Trägheitsmasse in der Translation. Im Gegensatz zur Masse hängt das Trägheitsmoment jedoch von der Geometrie des Körpers und der Verteilung seiner Masse in Bezug auf die Rotationsachse ab. Daher ist seine Berechnung für jede Situation, die modelliert werden soll, unerlässlich.
Variablen
Berechnungen
Berechnungen
Gleichungen
Die Arbeits Varianz ($\Delta W$), die erforderlich ist, damit ein Objekt von die Anfängliche Winkelgeschwindigkeit ($\omega_0$) auf die Winkelgeschwindigkeit ($\omega$) wechselt, wird durch das Anwenden eines der Drehmoment ($T$) erzeugt, das eine Winkelverschiebung die Differenz von Winkel ($\Delta\theta$) verursacht, gemäß:
| $ \Delta W = T \Delta\theta $ |
Anwendung des zweiten Newtonschen Gesetzes für Rotation in Bezug auf der Trägheitsmoment für Achse, die nicht durch das CM verläuft ($I$) und die Mittlere Winkelbeschleunigung ($\bar{\alpha}$):
| $ T = I \alpha $ |
kann dieser Ausdruck umgeschrieben werden als:
$\Delta W = I \alpha \Delta\theta$
oder unter Verwendung von die Unterschied in der Winkelgeschwindigkeiten ($\Delta\omega$) und der Abgelaufene Zeit ($\Delta t$):
| $ \bar{\alpha} \equiv \displaystyle\frac{ \Delta\omega }{ \Delta t }$ |
ergibt sich:
$\Delta W = I\displaystyle\frac{\Delta\omega}{\Delta t} \Delta\theta$
Durch Verwendung der Definition von die Mittlere Winkelgeschwindigkeit ($\bar{\omega}$) und der Abgelaufene Zeit ($\Delta t$):
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
resultiert:
$\Delta W = I\displaystyle\frac{\Delta\omega}{\Delta t} \Delta\theta = I\omega \Delta\omega$
wobei die Unterschied in der Winkelgeschwindigkeiten ($\Delta\omega$) sich ausdrückt als:
| $ \Delta\omega = \omega_2 - \omega_1 $ |
Andererseits kann die Winkelgeschwindigkeit durch die durchschnittliche Winkelgeschwindigkeit angenähert werden:
$\bar{\omega}=\displaystyle\frac{\omega_1 + \oemga_2}{2}$
Durch die Kombination beider Ausdrücke ergibt sich:
$\Delta W = I \omega \Delta\omega = I(\omega_2 - \omega_1) \displaystyle\frac{(\omega_1 + \omega_2)}{2} = \displaystyle\frac{I}{2}(\omega_2^2 - \omega_1^2)$
Daher ergibt sich der Energieänderungsausdruck:
$\Delta W = \displaystyle\frac{I}{2}\omega_2^2 - \displaystyle\frac{I}{2}\omega_1^2$
Damit kann die Rotationskinetik wie folgt definiert werden:
| $ K_r =\displaystyle\frac{1}{2} I \omega ^2$ |
(ID 3255)
Das Trägheitsmoment einer Stange, die sich um eine senkrechte ($\perp$) Achse dreht, die durch das Zentrum verl uft, wird ermittelt, indem der K rper in kleine Volumeneinheiten unterteilt und sie summiert werden:
| $ I =\displaystyle\int_V r ^2 \rho dV $ |
was zu folgendem Ergebnis führt:
| $ I_{CM} =\displaystyle\frac{1}{12} m l ^2$ |
.
(ID 4432)
Das Tr gheitsmoment eines Quaders, der sich um eine Achse dreht, die durch sein Zentrum verl uft, wird ermittelt, indem der K rper in kleine Volumeneinheiten unterteilt und sie summiert werden:
| $ I =\displaystyle\int_V r ^2 \rho dV $ |
was zu folgendem Ergebnis f hrt:
| $ I_{CM} =\displaystyle\frac{1}{12} m ( a ^2+ b ^2)$ |
.
(ID 4433)
Das Trägheitsmoment eines Zylinders, der sich um eine zur Hauptachse parallele Achse ($\parallel$) dreht und die durch das Zentrum verläuft, wird ermittelt, indem der Körper in kleine Volumeneinheiten unterteilt und sie summiert werden:
| $ I =\displaystyle\int_V r ^2 \rho dV $ |
was zu folgendem Ergebnis führt:
| $ I_{CM} =\displaystyle\frac{1}{2} m r_c ^2$ |
.
(ID 4434)
Das Tr gheitsmoment eines Zylinders, der sich um eine senkrechte ($\perp$) Achse dreht, die durch das Zentrum verl uft, wird ermittelt, indem der K rper in kleine Volumeneinheiten unterteilt und sie summiert werden:
| $ I =\displaystyle\int_V r ^2 \rho dV $ |
was zu folgendem Ergebnis f hrt:
| $ I_{CM} =\displaystyle\frac{1}{12} m ( h ^2+3 r_c ^2)$ |
.
(ID 4435)
Das Tr gheitsmoment einer Kugel, die sich um eine Achse dreht, die durch ihr Zentrum verl uft, wird durch die Segmentierung des K rpers in kleine Volumeneinheiten und deren Addition gewonnen:
| $ I =\displaystyle\int_V r ^2 \rho dV $ |
was zu folgendem Ergebnis f hrt:
| $ I_{CM} =\displaystyle\frac{2}{5} m r_e ^2$ |
.
(ID 4436)
Beispiele
(ID 15604)
Ein Balken mit Masse $m$ und L nge $l$, der um sein Zentrum rotiert, das mit dem Schwerpunkt bereinstimmt:

(ID 10962)
Die Drehung eines Zylinders mit Masse $m$ und Radius $r$ um die Achse des Zylinders, wobei sich der Schwerpunkt (CM) in halber H he befindet:

(ID 10964)
In dieser Situation rotiert ein Zylinder mit Masse $m$, Radius $r$ und H he $h$ um eine Achse, die senkrecht zu seiner eigenen Achse verl uft. Diese Achse verl uft durch den Mittelpunkt der L nge des Zylinders, wo sich der Schwerpunkt (CM) befindet:

(ID 10965)
Eine Kugel mit der Masse $m$ und dem Radius $r$ rotiert um ihren Schwerpunkt, der sich im geometrischen Zentrum befindet:

(ID 10490)
Ein rechtwinkliges Quader mit der Masse $m$ und den Seitenl ngen $a$ und $b$, das senkrecht zur Rotationsachse steht, dreht sich um seinen Schwerpunkt, der sich im geometrischen Zentrum des K rpers befindet:

(ID 10973)
Im Fall eines rechtwinkligen Quaders mit Masse $m$ und Seitenl nge $a$ befindet sich der Schwerpunkt im geometrischen Zentrum:

(ID 10963)
(ID 15606)
ID:(1417, 0)
