Kinetische Rotationsenergie
Storyboard 
Die kinetische Rotationsenergie ist eine Funktion der Winkelgeschwindigkeit, die durch die Anwendung eines Drehmoments über eine bestimmte Zeit erreicht wird, während ein bestimmter Winkel durchlaufen wird.Daher ist die Rotationskinetik proportional zum Trägheitsmoment des Objekts und dem Quadrat der Winkelgeschwindigkeit.
ID:(2080, 0)
In einen Kanal fließen
Konzept 
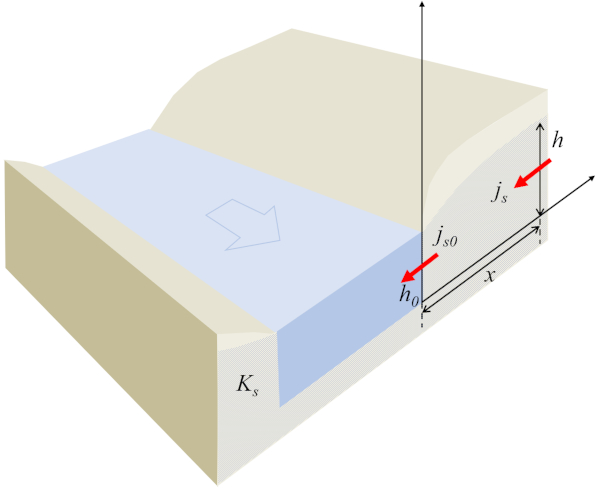
Im Fall des Flusses in Richtung eines Kanals kann das System eindimensional modelliert werden, wobei die Höhe der Wassersäule am Boden ($h$) eine Funktion von die Position der Wassersäule am Boden ($x$) ist, die die Flussdichte ($j_s$) repräsentiert und die Bedingung erfüllt
| $ h j_s = h_0 j_{s0} $ |
mit der Strömung an einem Referenzpunkt ($j_{s0}$) und die Referenzhöhe der Wassersäule ($h_0$), die das Profil des Wassers im Boden definieren:
None
Der Schlüssel zu dieser Gleichung besteht darin, dass das Produkt aus die Höhe der Wassersäule am Boden ($h$) und die Flussdichte ($j_s$) immer konstant sein muss. In diesem Sinne, wenn die Höhe der Wassersäule am Boden ($h$) steigt, sinkt die Flussdichte ($j_s$) und umgekehrt. Das Vorzeichen bleibt dabei immer gleich; daher wird der Fluss in Richtung des Kanals, d.h., der negative Fluss, nur auftreten, wenn der Grundwasserspiegel höher ist als der des Kanals. Wenn die Flüssigkeit dem Kanal näher kommt, sinkt der Grundwasserspiegel, was zu einer Zunahme der Flussdichte führt.
ID:(15104, 0)
Fließhöhenlösung in Richtung eines Kanals
Konzept 
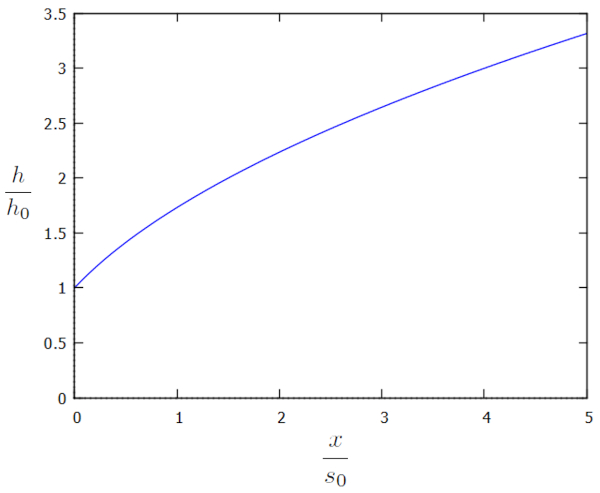
Die Lösung der eindimensionalen Strömungsgleichung in Richtung eines Kanals, bei der die Höhe der Wassersäule am Boden ($h$) als Funktion von die Referenzhöhe der Wassersäule ($h_0$) und die Position der Wassersäule am Boden ($x$) am Rand des Kanals zusammen mit der Charakteristische Länge der Strömung im Boden ($s_0$) berechnet wird, hat folgende Form:
| $ \displaystyle\frac{ h }{ h_0 } = \sqrt{1 + \displaystyle\frac{ 2 x }{ s_0 }} $ |
Diese Lösung wird graphisch in Abhängigkeit von den zusätzlichen Faktoren $h/h_0$ und $x/s_0$ wie folgt dargestellt:
None
Das Profil zeigt, dass die Höhe der Wassersäule fernab des Kanals deutlich hoch ist. Aufgrund der Wasserentnahme durch den Kanal beginnt diese Höhe jedoch abzunehmen, bis sie den Rand des Kanals erreicht. Dynamisch bestimmt die Flussdichte ($j_s$) die Menge des in den Kanal fließenden Wassers, während sich die Referenzhöhe der Wassersäule ($h_0$) allmählich anpasst, bis es einen Gleichgewichtszustand erreicht. Mit anderen Worten, wenn der Wert von die Referenzhöhe der Wassersäule ($h_0$) im Verhältnis zur Gesamtmenge des ankommenden Wassers zu niedrig ist, erhöht er sich, und wenn er zu hoch ist, nimmt er ab. Auf diese Weise nimmt die Referenzhöhe der Wassersäule ($h_0$) den Wert an, der die Menge des eintreffenden Wassers mit der Menge des durch den Kanal fließenden Wassers ausgleicht.
ID:(15109, 0)
Flussdichtelösung in Richtung eines Kanals
Konzept 
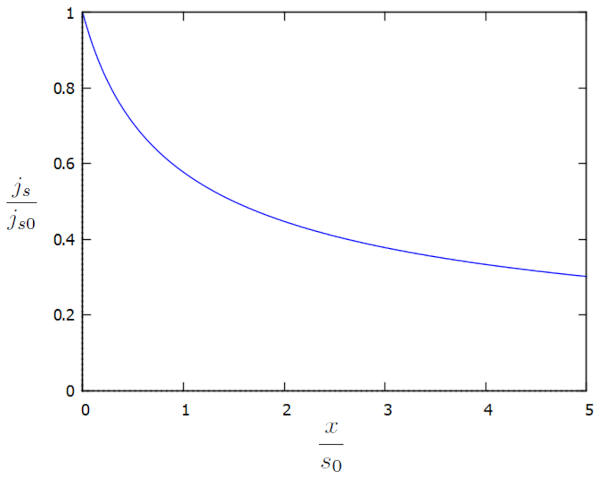
Die erhaltene Lösung für die Höhe und die Parameter der Strömung an einem Referenzpunkt ($j_{s0}$) und die Referenzhöhe der Wassersäule ($h_0$) zeigt, dass die Flussdichte ($j_s$) wie folgt berechnet wird:
| $ \displaystyle\frac{ j_s }{ j_{s0} } = \displaystyle\frac{1}{\sqrt{1 + \displaystyle\frac{ 2 x }{ s_0 }}} $ |
Wir können die Flussdichte ($j_s$) graphisch in Abhängigkeit von den zusätzlichen Faktoren $j_s/j_{s0}$ und $x/s_0$ wie folgt darstellen:
None
Es fällt auf, dass die Flussdichte ($j_s$) weiter zunimmt, je näher wir dem Kanal kommen, da die Höhe der Wassersäule am Boden ($h$) abnimmt. Dieser Anstieg ist erforderlich, um die Fließgeschwindigkeit in die Flussdichte ($j_s$) aufrechtzuerhalten oder alternativ, um sie zu erhöhen.
ID:(15110, 0)
Rotationskinetische Energie
Modell 
Im Falle der Rotation eines Körpers kann analog zur Translation eine kinetische Energie definiert werden, die jedoch mit der Rotation verbunden ist. So wie die translatorische kinetische Energie von der Masse und der linearen Geschwindigkeit abhängt, gibt es auch in der Rotation eine äquivalente Rolle der Trägheit. Diese hängt zwar von der Masse ab, wird jedoch zusätzlich durch die Entfernung dieser Masse zur Rotationsachse bestimmt. Auf diese Weise wird das Konzept des Trägheitsmoments eingeführt, das eine analoge Rolle zur Trägheitsmasse spielt. Das Trägheitsmoment wird mit dem Quadrat der Winkelgeschwindigkeit multipliziert, und indem man dieses Produkt durch zwei teilt, erhält man die Rotationskinetische Energie.
Variablen
Berechnungen
Berechnungen
Gleichungen
Die Definition der durchschnittlichen Winkelbeschleunigung basiert auf dem zur ckgelegten Winkel
| $ \Delta\omega = \omega_2 - \omega_1 $ |
und der verstrichenen Zeit
| $ \Delta t \equiv t - t_0 $ |
Die Beziehung zwischen beiden wird als die durchschnittliche Winkelbeschleunigung definiert
| $ \bar{\alpha} \equiv \displaystyle\frac{ \Delta\omega }{ \Delta t }$ |
innerhalb dieses Zeitintervalls.
(ID 3234)
Da das Moment gleich ist
| $ L = I \omega $ |
folgt daraus, dass im Fall, dass sich das Tr gheitsmoment nicht mit der Zeit ndert,
$T=\displaystyle\frac{dL}{dt}=\displaystyle\frac{d}{dt}(I\omega) = I\displaystyle\frac{d\omega}{dt} = I\alpha$
was bedeutet, dass
| $ T = I \alpha $ |
.
(ID 3253)
Die Arbeits Varianz ($\Delta W$), die erforderlich ist, damit ein Objekt von die Anfängliche Winkelgeschwindigkeit ($\omega_0$) auf die Winkelgeschwindigkeit ($\omega$) wechselt, wird durch das Anwenden eines der Drehmoment ($T$) erzeugt, das eine Winkelverschiebung die Differenz von Winkel ($\Delta\theta$) verursacht, gemäß:
| $ \Delta W = T \Delta\theta $ |
Anwendung des zweiten Newtonschen Gesetzes für Rotation in Bezug auf der Trägheitsmoment für Achse, die nicht durch das CM verläuft ($I$) und die Mittlere Winkelbeschleunigung ($\bar{\alpha}$):
| $ T = I \bar{\alpha} $ |
kann dieser Ausdruck umgeschrieben werden als:
$\Delta W = I \alpha \Delta\theta$
oder unter Verwendung von die Unterschied in der Winkelgeschwindigkeiten ($\Delta\omega$) und der Abgelaufene Zeit ($\Delta t$):
| $ \bar{\alpha} \equiv \displaystyle\frac{ \Delta\omega }{ \Delta t }$ |
ergibt sich:
$\Delta W = I\displaystyle\frac{\Delta\omega}{\Delta t} \Delta\theta$
Durch Verwendung der Definition von die Mittlere Winkelgeschwindigkeit ($\bar{\omega}$) und der Abgelaufene Zeit ($\Delta t$):
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
resultiert:
$\Delta W = I\displaystyle\frac{\Delta\omega}{\Delta t} \Delta\theta = I\omega \Delta\omega$
wobei die Unterschied in der Winkelgeschwindigkeiten ($\Delta\omega$) sich ausdrückt als:
| $ \Delta\omega = \omega_2 - \omega_1 $ |
Andererseits kann die Winkelgeschwindigkeit durch die durchschnittliche Winkelgeschwindigkeit angenähert werden:
$\bar{\omega}=\displaystyle\frac{\omega_1 + \oemga_2}{2}$
Durch die Kombination beider Ausdrücke ergibt sich:
$\Delta W = I \omega \Delta\omega = I(\omega_2 - \omega_1) \displaystyle\frac{(\omega_1 + \omega_2)}{2} = \displaystyle\frac{I}{2}(\omega_2^2 - \omega_1^2)$
Daher ergibt sich der Energieänderungsausdruck:
$\Delta W = \displaystyle\frac{I}{2}\omega_2^2 - \displaystyle\frac{I}{2}\omega_1^2$
Damit kann die Rotationskinetik wie folgt definiert werden:
| $ K_r =\displaystyle\frac{1}{2} I \omega ^2$ |
(ID 3255)
Die Arbeits Varianz ($\Delta W$), die erforderlich ist, damit ein Objekt von die Anfängliche Winkelgeschwindigkeit ($\omega_0$) auf die Winkelgeschwindigkeit ($\omega$) wechselt, wird durch das Anwenden eines der Drehmoment ($T$) erzeugt, das eine Winkelverschiebung die Differenz von Winkel ($\Delta\theta$) verursacht, gemäß:
| $ \Delta W = T \Delta\theta $ |
Anwendung des zweiten Newtonschen Gesetzes für Rotation in Bezug auf der Trägheitsmoment für Achse, die nicht durch das CM verläuft ($I$) und die Mittlere Winkelbeschleunigung ($\bar{\alpha}$):
| $ T = I \bar{\alpha} $ |
kann dieser Ausdruck umgeschrieben werden als:
$\Delta W = I \alpha \Delta\theta$
oder unter Verwendung von die Unterschied in der Winkelgeschwindigkeiten ($\Delta\omega$) und der Abgelaufene Zeit ($\Delta t$):
| $ \bar{\alpha} \equiv \displaystyle\frac{ \Delta\omega }{ \Delta t }$ |
ergibt sich:
$\Delta W = I\displaystyle\frac{\Delta\omega}{\Delta t} \Delta\theta$
Durch Verwendung der Definition von die Mittlere Winkelgeschwindigkeit ($\bar{\omega}$) und der Abgelaufene Zeit ($\Delta t$):
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
resultiert:
$\Delta W = I\displaystyle\frac{\Delta\omega}{\Delta t} \Delta\theta = I\omega \Delta\omega$
wobei die Unterschied in der Winkelgeschwindigkeiten ($\Delta\omega$) sich ausdrückt als:
| $ \Delta\omega = \omega_2 - \omega_1 $ |
Andererseits kann die Winkelgeschwindigkeit durch die durchschnittliche Winkelgeschwindigkeit angenähert werden:
$\bar{\omega}=\displaystyle\frac{\omega_1 + \oemga_2}{2}$
Durch die Kombination beider Ausdrücke ergibt sich:
$\Delta W = I \omega \Delta\omega = I(\omega_2 - \omega_1) \displaystyle\frac{(\omega_1 + \omega_2)}{2} = \displaystyle\frac{I}{2}(\omega_2^2 - \omega_1^2)$
Daher ergibt sich der Energieänderungsausdruck:
$\Delta W = \displaystyle\frac{I}{2}\omega_2^2 - \displaystyle\frac{I}{2}\omega_1^2$
Damit kann die Rotationskinetik wie folgt definiert werden:
| $ K_r =\displaystyle\frac{1}{2} I \omega ^2$ |
(ID 3255)
(ID 4440)
(ID 10301)
Unter Verwendung der klassischen Definition von Energie, wobei die Arbeits Varianz ($\Delta W$) aus die Kraft mit konstanter Masse ($F$) und die Zurückgelegte Strecke in einer Zeit ($\Delta s$) berechnet wird gemäß:
| $ \Delta W = F \Delta s $ |
Im Fall der Rotation steht die Kraft senkrecht zu der Radius ($r$) und erzeugt der Drehmoment ($T$), was ausgedrückt wird durch:
| $ T = r F $ |
Da der zurückgelegte Bogen gleich der Radius ($r$) mal die Differenz von Winkel ($\Delta\theta$) ist:
| $ \Delta s=r \Delta\theta $ |
ergibt sich:
$\Delta W = \vec{F}\cdot\Delta\vec{s} = F\Delta s = F r\Delta\theta = T\Delta\theta$
Das heißt:
| $ \Delta W = T \Delta\theta $ |
(ID 12550)
Beispiele
(ID 15604)
(ID 15606)
ID:(2144, 0)
