Utilizador:
Arco percorrido ao girar
Audio 
Se observarmos um círculo, o seu perímetro será $2\pi r$, com o rádio ($r$). Se tivermos uma variação de ângulo ($\Delta\theta$), isso representa uma fração da circunferência total, dada pela expressão:
$\displaystyle\frac{\Delta\theta}{2\pi}$
la distância percorrida em um tempo ($\Delta s$) corresponde ao arco sob la variação de ângulo ($\Delta\theta$) que pode ser calculado como essa fração do perímetro total do círculo:
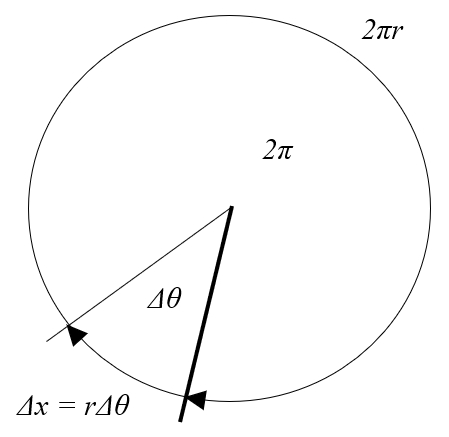
Para estes cálculos, é crucial que o ângulo seja expresso em radianos.
ID:(9879, 0)
Rotação
Descrição
Para descrever o movimento de um corpo, não é apenas necessário definir seu deslocamento, mas também indicar como ele gira em torno de um eixo. Portanto, é fundamental descrever seu eixo e a rotação que realiza em torno dele.
Variáveis
Cálculos
para 
,
depois, selecione a variável: 
para 
Cálculos
Variáve
Dado
Calcular
Objetivo :
Equação
A ser usado
Equações
Se partirmos de la velocidade ($s_0$) e quisermos calcular la distância percorrida em um tempo ($\Delta s$), é necessário definir um valor para la posição ($s$).
Em um sistema unidimensional, la distância percorrida em um tempo ($\Delta s$) é obtido simplesmente subtraindo la velocidade ($s_0$) de la posição ($s$), resultando em:
| $ \Delta s = s - s_0 $ |
(ID 4352)
Se um objeto est a uma dist ncia igual a o rádio ($r$) de um eixo e realiza uma rota o de uma variação de ângulo ($\Delta\theta$), que com o ângulo ($\theta$) e o ângulo inicial ($\theta_0$)
| $ \Delta\theta = \theta_2 - \theta_1 $ |
ele ter percorrido um arco la distância percorrida em um tempo ($\Delta s$), que com la posição ($s$) e la velocidade ($s_0$)
| $ \Delta s = s - s_0 $ |
Este arco pode ser calculado multiplicando o rádio ($r$) pelo ngulo, ou seja,
| $ \Delta s=r \Delta\theta $ |
.
(ID 5302)
Exemplos
A rota o leva a uma mudan a de la variação de ângulo ($\Delta\theta$), que est associada posi o final o ângulo ($\theta$). Atrav s do raio de rota o, essa mudan a est associada a um arco percorrido de la distância percorrida em um tempo ($\Delta s$) a la posição ($s$).
(ID 15385)
Para definir uma rota o no espa o tridimensional, necess rio primeiro especificar o eixo em torno do qual ocorrer o movimento. Uma vez que o eixo tenha sido definido, pode-se indicar o ngulo de rota o que deve ser aplicado ao corpo em torno desse eixo. importante notar que a dire o do eixo definida pela linha reta que o atravessa e, por conven o, geralmente representada por um vetor unit rio. Da mesma forma, o ngulo de rota o medido em radianos e pode ser positivo ou negativo, dependendo da dire o de rota o desejada.
(ID 4382)
Ao descrever um movimento de rota o, n o podemos trabalhar com dist ncia da mesma maneira que fazemos ao descrever um movimento de transla o.
• Nesse caso, primeiro devemos determinar a posi o do eixo (vetor) de rota o.
• Em seguida, devemos determinar a dist ncia entre o objeto e o eixo de rota o.
• Finalmente, devemos estimar o ngulo de rota o do objeto ao redor do eixo.
Em um movimento de rota o, o raio permanece constante. Quaisquer mudan as no raio n o fazem parte da rota o, mas sim de uma transla o que o objeto possa realizar radialmente.
(ID 4967)
A situa o mais simples aquela em que o corpo gira em torno do seu pr prio eixo. Neste caso, o eixo do corpo coincide com o eixo de rota o, e o ngulo define a pr pria rota o:
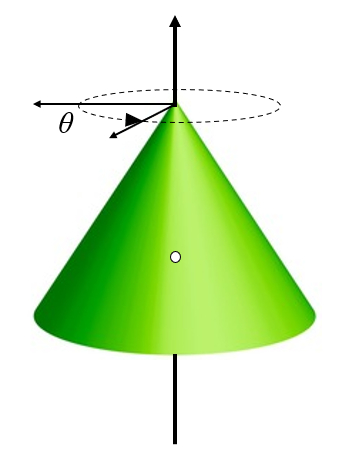
(ID 10537)
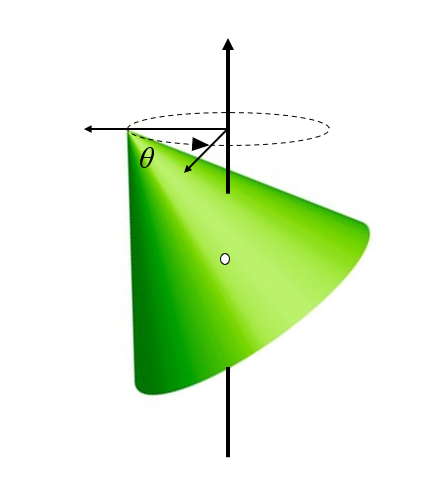
A situa o mais geral ocorre quando o eixo do corpo n o coincide com o eixo de rota o. Nesse caso, podemos pensar em uma rota o pr via do corpo de modo que seu eixo forme um ngulo em rela o ao eixo de rota o:
(ID 11405)
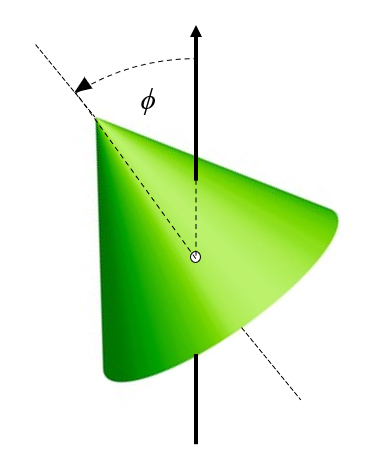
Quando um corpo gira e seu eixo n o coincide com o eixo de rota o, ele sofre uma precess o em torno do eixo de rota o:
(ID 11406)
Al m da coincid ncia ou n o do eixo do corpo com o eixo de rota o, existe tamb m a situa o em que o eixo de rota o passa pelo centro geom trico do corpo:
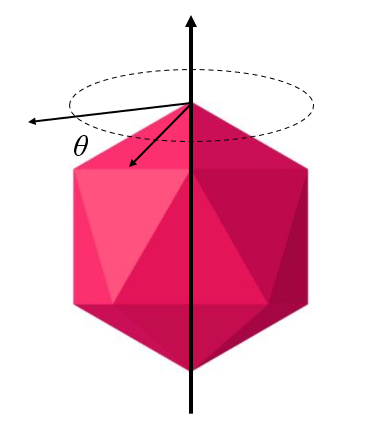
(ID 10299)
Se o eixo de rota o n o passa pelo centro do corpo, este n o apenas girar em torno de seu pr prio eixo, mas tamb m orbitar em torno do eixo de rota o:
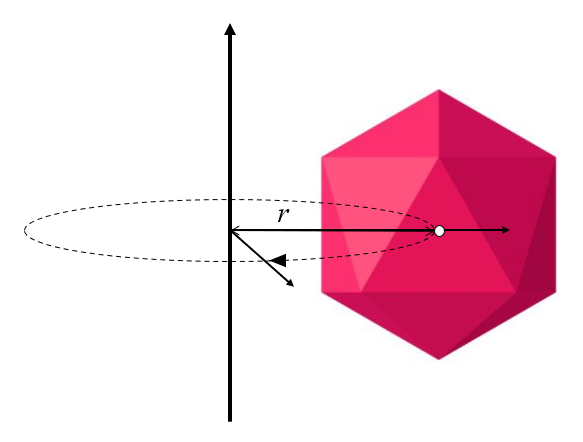
Esta a situa o mais geral que precisa ser descrita quando o corpo realiza uma rota o.
(ID 10541)
Se observarmos um c rculo, o seu per metro ser $2\pi r$, com o rádio ($r$). Se tivermos uma variação de ângulo ($\Delta\theta$), isso representa uma fra o da circunfer ncia total, dada pela express o:
$\displaystyle\frac{\Delta\theta}{2\pi}$
la distância percorrida em um tempo ($\Delta s$) corresponde ao arco sob la variação de ângulo ($\Delta\theta$) que pode ser calculado como essa fra o do per metro total do c rculo:
Para estes c lculos, crucial que o ngulo seja expresso em radianos.
(ID 9879)
Na f sica, comum utilizar radianos em vez de graus para medir ngulos em rota es. Isso se deve ao fato de que, nesse tipo de movimento, os objetos que orbitam percorrem dist ncias que correspondem a arcos de um c rculo. Para determinar a velocidade do objeto, necess rio calcular o comprimento do arco percorrido, o que f cil de fazer se o raio da rbita e o ngulo percorrido em radianos forem conhecidos. Por essa raz o, geralmente se trabalha com medidas de ngulos em radianos para evitar a necessidade de convers o constante entre graus e radianos ao realizar c lculos desse tipo.
(ID 311)
(ID 15386)
ID:(595, 0)