Arc traveled when rotating
Audio 
If you observe a circle, its perimeter will be $2\pi r$, with the radius ($r$). If you have a angle variation ($\Delta\theta$), it represents a fraction of the total circumference, given by the expression:
$\displaystyle\frac{\Delta\theta}{2\pi}$
the distance traveled in a time ($\Delta s$) corresponding to the arc under the angle variation ($\Delta\theta$) which can be calculated as this fraction of the total perimeter of the circle:
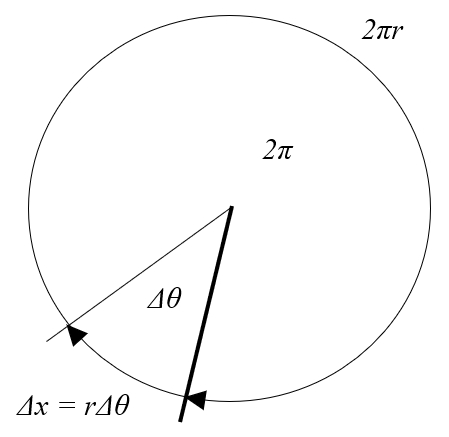
For these calculations, it is crucial that the angle is expressed in radians.
ID:(9879, 0)
Rotation
Description 
To describe the motion of a body, it is not only necessary to define its displacement but also to indicate how it rotates around an axis. Therefore, it is essential to describe its axis and the rotation it performs around it.
Variables
Calculations
Calculations
Equations
If we start from the starting position ($s_0$) and want to calculate the distance traveled in a time ($\Delta s$), we need to define a value for the position ($s$).
In a one-dimensional system, the distance traveled in a time ($\Delta s$) is simply obtained by subtracting the starting position ($s_0$) from the position ($s$), resulting in:
| $ \Delta s = s - s_0 $ |
(ID 4352)
If an object is at a distance equal to the radius ($r$) from an axis and rotates by ERROR:6066.1, which with the angle ($\theta$) and the initial Angle ($\theta_0$) is
| $ \Delta\theta = \theta_2 - \theta_1 $ |
it will have traveled an arc length the distance traveled in a time ($\Delta s$), which with the position ($s$) and the starting position ($s_0$) is
| $ \Delta s = s - s_0 $ |
This arc length can be calculated by multiplying the radius ($r$) by the angle, that is,
| $ \Delta s=r \Delta\theta $ |
.
(ID 5302)
Examples
The rotation leads to a change of the angle variation ($\Delta\theta$) which is associated with the final position the angle ($\theta$). Through the radius of rotation, this change is associated with an arc traversed from the distance traveled in a time ($\Delta s$) to the position ($s$).
(ID 15385)
To define a rotation in three-dimensional space, it is necessary first to specify the axis around which the movement will occur. Once the axis has been defined, the angle of rotation that should be applied to the body around that axis can be indicated. It is important to note that the direction of the axis is defined by the straight line that passes through it and, by convention, is usually represented by a unit vector. Likewise, the angle of rotation is measured in radians and can be positive or negative, depending on the direction of rotation that is desired.
(ID 4382)
When describing a rotational motion, we cannot work with distance in the same way we do when describing translational motion.
• In this case, we must first determine the position of the axis (vector) of rotation.
• Then, we must determine the distance between the object and the axis of rotation.
• Finally, we must estimate the angle of rotation of the object around the axis.
In a rotational motion, the radius remains constant. Any changes in the radius are not part of the rotation, but rather a translation that the object may perform radially.
(ID 4967)
The simplest situation is when the body rotates around its own axis. In this case, the body's axis aligns with the axis of rotation, and the angle defines the rotation itself:
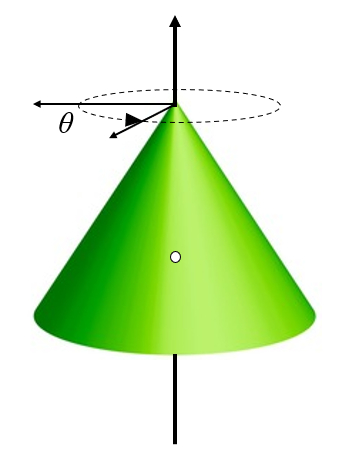
(ID 10537)
The more general situation occurs when the body's axis does not align with the axis of rotation. In this case, we can envision a prior rotation of the body so that its axis forms an angle with respect to the axis of rotation:
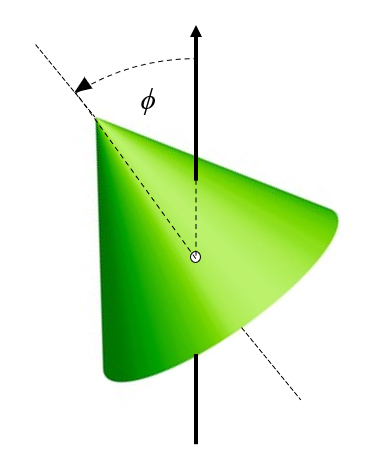
(ID 11405)
When a body rotates and its axis does not align with the axis of rotation, it undergoes a precession around the axis of rotation:
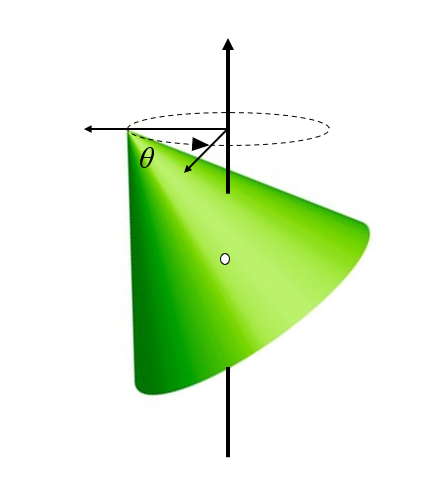
(ID 11406)
Apart from whether or not the body's axis coincides with the axis of rotation, there's also the situation where the axis of rotation passes through the body's geometric center:
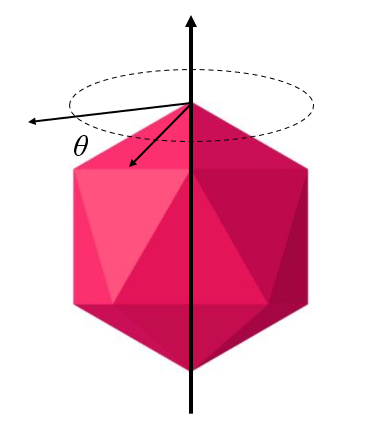
(ID 10299)
If the axis of rotation doesn't pass through the center of the body, it will not only rotate around its own axis but also orbit around the axis of rotation:
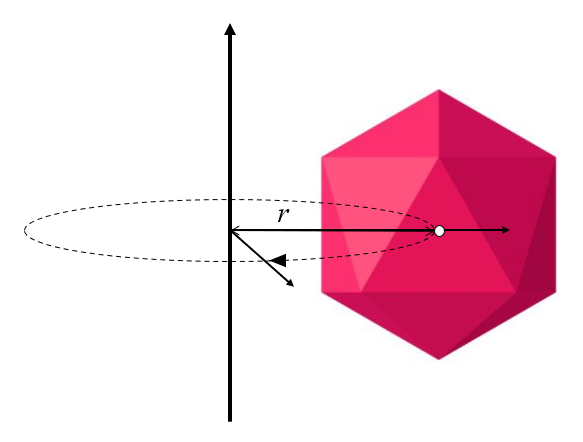
This is the most general situation that needs to be described when the body undergoes rotation.
(ID 10541)
If you observe a circle, its perimeter will be $2\pi r$, with the radius ($r$). If you have a angle variation ($\Delta\theta$), it represents a fraction of the total circumference, given by the expression:
$\displaystyle\frac{\Delta\theta}{2\pi}$
the distance traveled in a time ($\Delta s$) corresponding to the arc under the angle variation ($\Delta\theta$) which can be calculated as this fraction of the total perimeter of the circle:

For these calculations, it is crucial that the angle is expressed in radians.
(ID 9879)
In physics, it is common to use radians instead of degrees to measure angles in rotations. This is because in these types of movements, the objects that orbit cover distances that correspond to arcs of a circle. To determine the velocity of the object, it is necessary to calculate the length of the arc covered, which is easy to do if the radius of the orbit and the angle covered in radians are known. For this reason, angles are generally measured in radians to avoid the need for constant conversion between degrees and radians when performing calculations of this type.
(ID 311)
(ID 15386)
ID:(595, 0)
