Utilisateur:
Arc parcouru lors de la rotation
Audio 
Si l'on observe un cercle, son périmètre sera de $2\pi r$, avec le radio ($r$). Si l'on a une variation d'angle ($\Delta\theta$), cela représente une fraction du périmètre total, donnée par l'expression :
$\displaystyle\frac{\Delta\theta}{2\pi}$
a distance parcourue en un temps ($\Delta s$) correspondant à l'arc sous a variation d'angle ($\Delta\theta$) qui peut être calculé comme cette fraction du périmètre total du cercle :
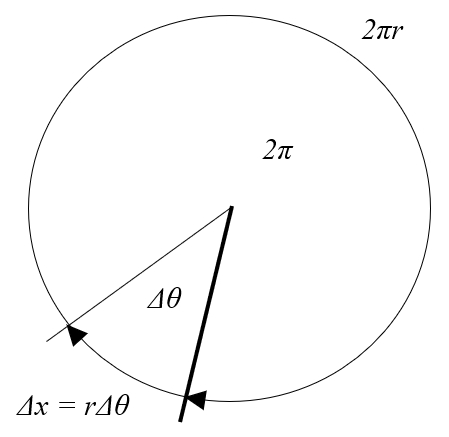
Pour ces calculs, il est crucial que l'angle soit exprimé en radians.
ID:(9879, 0)
Rotation
Description
Pour décrire le mouvement d'un corps, il ne suffit pas de définir son déplacement, il faut également indiquer comment il tourne autour d'un axe. Il est donc essentiel de décrire cet axe et la rotation qu'il effectue autour de celui-ci.
Variables
Calculs
à 
,
puis, sélectionnez la variable: 
à 
Calculs
Variable
Donnée
Calculer
Cible :
Équation
À utiliser
Équations
Si l’on part de a vitesse ($s_0$) et que l’on souhaite calculer a distance parcourue en un temps ($\Delta s$), il est nécessaire de définir une valeur pour a position ($s$).
Dans un système unidimensionnel, a distance parcourue en un temps ($\Delta s$) est simplement obtenu en soustrayant a vitesse ($s_0$) de a position ($s$), ce qui donne :
| $ \Delta s = s - s_0 $ |
(ID 4352)
Si un objet est une distance gale le radio ($r$) d'un axe et effectue une rotation en une variation d'angle ($\Delta\theta$), ce qui avec le angle ($\theta$) et le angle de départ ($\theta_0$) est
| $ \Delta\theta = \theta_2 - \theta_1 $ |
il aura parcouru un arc a distance parcourue en un temps ($\Delta s$), ce qui avec a position ($s$) et a vitesse ($s_0$) est
| $ \Delta s = s - s_0 $ |
Cet arc peut tre calcul en multipliant le radio ($r$) par l'angle, c'est- -dire
| $ \Delta s=r \Delta\theta $ |
.
(ID 5302)
Exemples
La rotation entra ne un changement de a variation d'angle ($\Delta\theta$) qui est associ la position finale le angle ($\theta$). travers le rayon de rotation, ce changement est li un arc parcouru de a distance parcourue en un temps ($\Delta s$) A position ($s$).
(ID 15385)
Pour d finir une rotation dans l'espace tridimensionnel, il est n cessaire tout d'abord de sp cifier l\'axe autour duquel le mouvement se produira. Une fois que l\'axe a t d fini, l\'angle de rotation qui doit tre appliqu au corps autour de cet axe peut tre indiqu . Il est important de noter que la direction de l\'axe est d finie par la ligne droite qui le traverse et, par convention, est g n ralement repr sent e par un vecteur unitaire. De m me, l\'angle de rotation est mesur en radians et peut tre positif ou n gatif, selon la direction de rotation souhait e.
(ID 4382)
Lorsque nous d crivons un mouvement de rotation, nous ne pouvons pas travailler avec la distance de la m me mani re que nous le faisons lorsque nous d crivons un mouvement de translation.
• Dans ce cas, nous devons d'abord d terminer la position de l'axe (vecteur) de rotation.
• Ensuite, nous devons d terminer la distance entre l\'objet et l\'axe de rotation.
• Enfin, nous devons estimer l\'angle de rotation de l\'objet autour de l\'axe.
Dans un mouvement de rotation, le rayon reste constant. Toute modification du rayon ne fait pas partie de la rotation, mais d\'une translation que l\'objet peut effectuer radialement.
(ID 4967)
La situation la plus simple est lorsque le corps tourne autour de son propre axe. Dans ce cas, l'axe du corps co ncide avec l'axe de rotation, et l'angle d finit la rotation elle-m me :
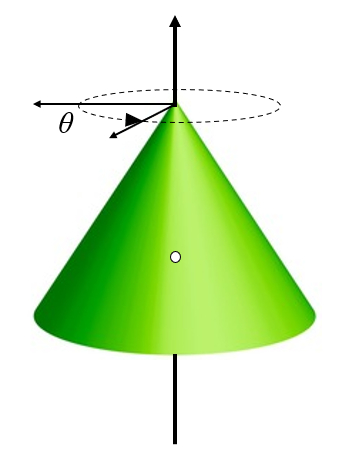
(ID 10537)
La situation la plus g n rale est lorsque l'axe du corps ne co ncide pas avec l'axe de rotation. Dans ce cas, on peut envisager une rotation pr alable du corps de sorte que son axe forme un angle par rapport l'axe de rotation :
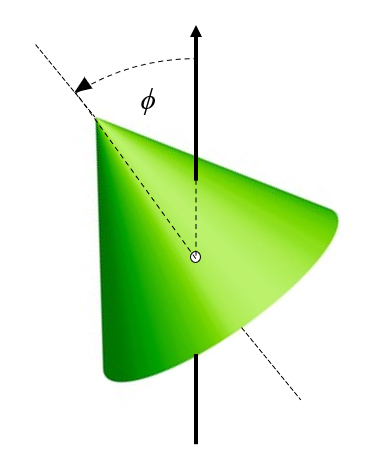
(ID 11405)
Lorsqu'un corps tourne et que son axe ne co ncide pas avec l'axe de rotation, il subit une pr cession autour de l'axe de rotation :
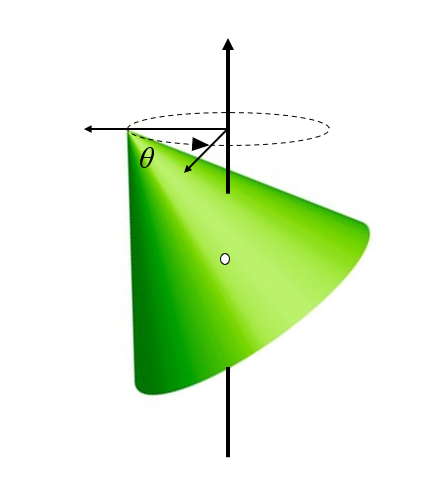
(ID 11406)
En dehors de la co ncidence ou non de l'axe du corps avec l'axe de rotation, il existe galement la situation o l'axe de rotation passe par le centre g om trique du corps :
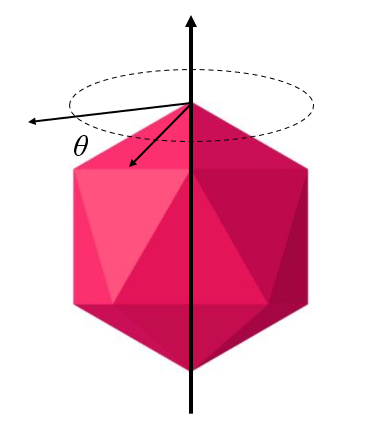
(ID 10299)
Si l'axe de rotation ne passe pas par le centre du corps, celui-ci ne tournera pas seulement autour de son propre axe, mais orbitera galement autour de l'axe de rotation :
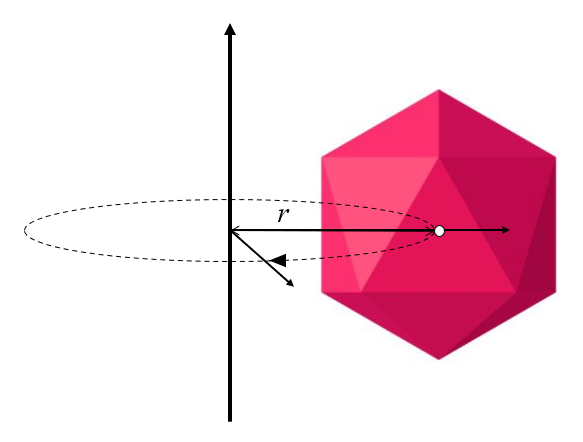
C'est la situation la plus g n rale qu'il faut d crire lorsque le corps effectue une rotation.
(ID 10541)
Si l'on observe un cercle, son p rim tre sera de $2\pi r$, avec le radio ($r$). Si l'on a une variation d'angle ($\Delta\theta$), cela repr sente une fraction du p rim tre total, donn e par l'expression :
$\displaystyle\frac{\Delta\theta}{2\pi}$
a distance parcourue en un temps ($\Delta s$) correspondant l'arc sous a variation d'angle ($\Delta\theta$) qui peut tre calcul comme cette fraction du p rim tre total du cercle :
Pour ces calculs, il est crucial que l'angle soit exprim en radians.
(ID 9879)
En physique, il est courant d'utiliser des radians plut t que des degr s pour mesurer les angles en rotation. Cela est d au fait que dans ce type de mouvement, les objets en orbite parcourent des distances qui correspondent des arcs d\'un cercle. Pour d terminer la vitesse de l\'objet, il est n cessaire de calculer la longueur de l\'arc parcouru, ce qui est facile faire si le rayon de l\'orbite et l\'angle parcouru en radians sont connus. Pour cette raison, les angles sont g n ralement mesur s en radians afin d\' viter la n cessit d\'une conversion constante entre les degr s et les radians lors des calculs de ce type.
(ID 311)
(ID 15386)
ID:(595, 0)