Flujo turbulento por tubos
Storyboard 
Si el número de Reynolds es superior a 2000, el flujo en un tubo se vuelve siempre inestable y termina siendo completamente turbulento. Con esto, ya no es posible usar la aproximación de flujo laminar viscoso que da origen a la ley de Hagen Poiseuille, y es necesario desarrollar un modelo alternativo.
El modelo que describe un flujo en el cual la viscosidad es irrelevante es el que da origen a la ecuación de Bernoulli. Sin embargo, este modelo asume que la densidad de energía se conserva. Una alternativa es asumir que las turbulencias llevan a una mezcla mediante la cual la densidad de energía no se conserva pero permanece constante. En tal caso, el flujo se puede modelar mediante una ecuación similar a la de Bernoulli, pero teniendo en cuenta una corrección debido a la homogeneización causada por la mezcla.
ID:(1970, 0)
Modelamiento de la turbulencia
Definición 
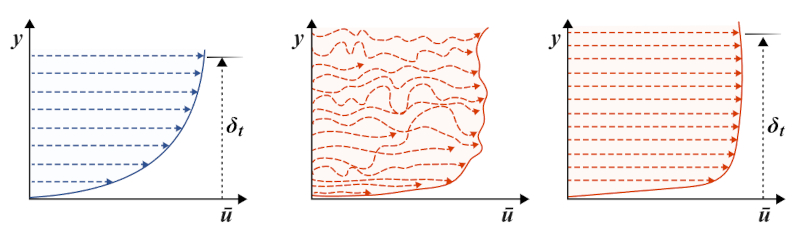
El flujo laminar se describe mediante "láminas" que se desplazan a diferentes velocidades de manera coordinada. En contraste, en el flujo turbulento no existen estas láminas. Los elementos del fluido son desviados, pueden cambiar de dirección y participar en movimientos circulares en gran medida de manera caótica.
La primera consecuencia de esto es que los parámetros del fluido tienden a mezclarse, lo que resulta en la desaparición de las diferencias de velocidad y la aparición de un tipo de velocidad media. De esta manera, al promediar el movimiento, surgen patrones estructurados, pero ya no provienen de elementos individuales del flujo, sino de una mezcla temporal. Como resultado, se obtiene nuevamente un perfil relativamente constante que se asemeja a los perfiles definidos en el flujo laminar, pero en este caso son valores promedio y ya no presentan grandes gradientes, siendo más uniformes.
ID:(14525, 0)
Diagrama de Moody
Imagen 
En 1944, Lewis Ferry Moody realizó mediciones del factor de fricción de Darcy-Weisbach en función del número de Reynolds y de la rugosidad relativa de la pared, lo que resultó en la creación del siguiente diagrama:
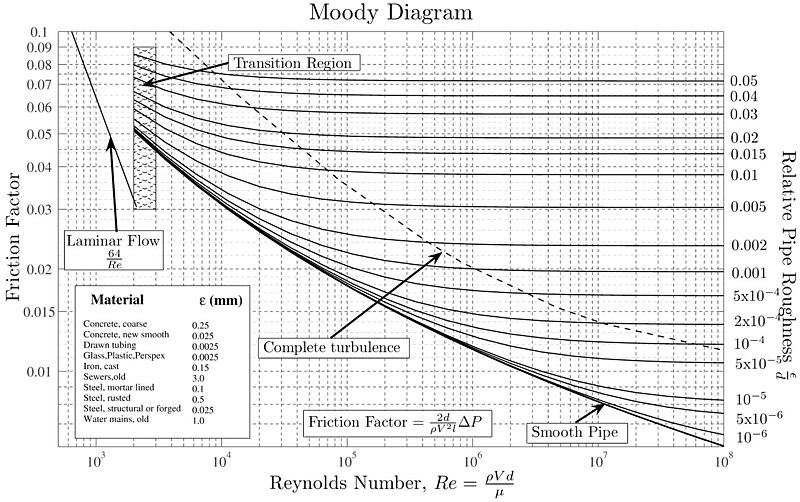
La rugosidad relativa se puede estimar considerando el tamaño de las rugosidades (altura de elementos que sobresalen o profundidades de hendiduras) en relación con el diámetro hidrodinámico.
Se observan dos comportamientos distintos:
• Para números de Reynolds inferiores a 2000, el factor de fricción de Darcy-Weisbach depende solo del número de Reynolds, siguiendo una relación de $64/Re$. Esto corresponde al régimen laminar.
• Para números de Reynolds superiores a 2000, se observa un comportamiento que depende tanto del número de Reynolds como de la rugosidad relativa de la superficie del tubo.
ID:(14528, 0)
Flujo en el límite laminar
Nota 
Si reemplazamos el factor de fricción de Darcy-Weisbach en el límite laminar, dado por
| $ f_D = \displaystyle\frac{64}{ Re }$ |
en la ecuación de Darcy-Weisbach, expresada como
| $ \Delta p = \displaystyle\frac{ \Delta L }{ D_H } f_D \displaystyle\frac{1}{2} \rho_w j_s ^2 $ |
y utilizamos la definición del número de Reynolds $Re$, podemos demostrar que el flujo está gobernado por
| $ J_V =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
que corresponde a la ecuación de Hagen-Poiseuille.
ID:(14530, 0)
Perfil de velocidad de flujo turbulento en tubo
Cita 
El perfil de velocidad en un flujo turbulento a través de un tubo muestra dos zonas distintas en función de la distancia a la superficie ($z$), donde $\delta$ es el espesor de la capa límite. En la zona cercana a la superficie ($z < \delta$), el flujo es esencialmente laminar, mientras que en la zona más alejada de la superficie ($z > \delta$), el flujo se vuelve turbulento.
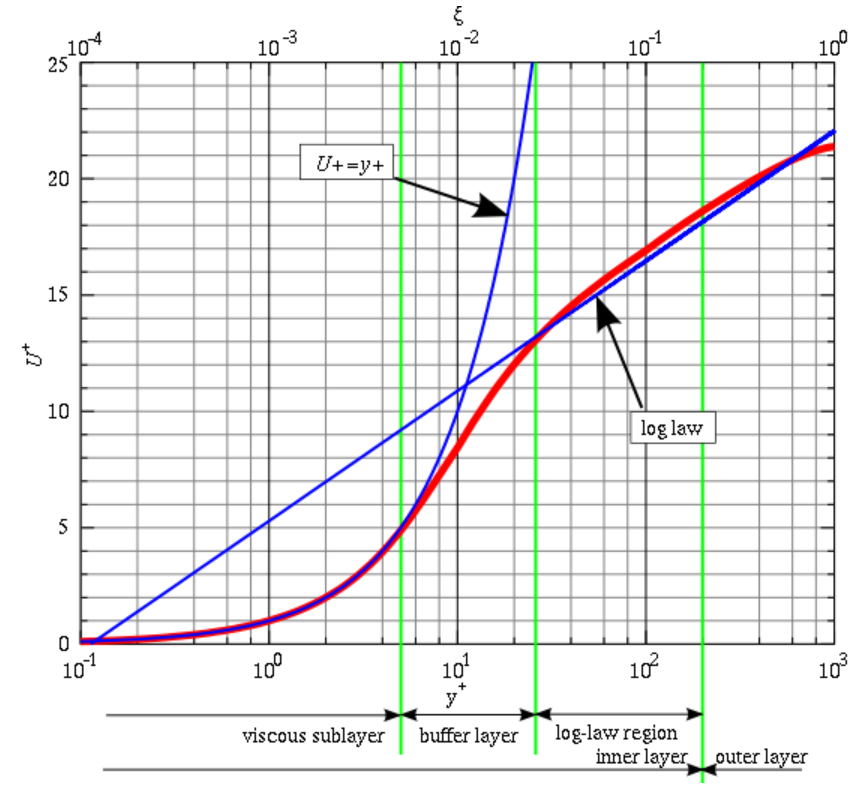
En la región laminar, la velocidad es proporcional a la distancia normalizada:
$u^+ = y^+$
Esta relación es similar al perfil de velocidad de Hagen-Poiseuille cerca de la pared y representa una aproximación lineal.
En la región turbulenta, el perfil de velocidad normalizado tiene una forma logarítmica:
$u^+ = \displaystyle\frac{1}{\kappa} \ln\left(\displaystyle\frac{y^+}{y_0}\right)$
Aquí, $\kappa$ es la constante de Karman (aproximadamente $0.41$) y $y_0\sim 1/8$ es la distancia normalizada en la que la velocidad sería cero. Sin embargo, es importante tener en cuenta que el ancho de la capa laminar, según el gráfico, es de aproximadamente 7.072 veces mayor que $y_0$.
ID:(14536, 0)
Flujo turbulento por tubos
Descripción 
Si el número de Reynolds es superior a 2000, el flujo en un tubo se vuelve siempre inestable y termina siendo completamente turbulento. Con esto, ya no es posible usar la aproximación de flujo laminar viscoso que da origen a la ley de Hagen Poiseuille, y es necesario desarrollar un modelo alternativo. El modelo que describe un flujo en el cual la viscosidad es irrelevante es el que da origen a la ecuación de Bernoulli. Sin embargo, este modelo asume que la densidad de energía se conserva. Una alternativa es asumir que las turbulencias llevan a una mezcla mediante la cual la densidad de energía no se conserva pero permanece constante. En tal caso, el flujo se puede modelar mediante una ecuación similar a la de Bernoulli, pero teniendo en cuenta una corrección debido a la homogeneización causada por la mezcla.
Variables
Cálculos
Cálculos
Ecuaciones
Si hay la diferencia de presión ($\Delta p$) entre dos puntos, como lo indica la ecuaci n:
| $ dp = p - p_0 $ |
podemos usar la presión de la columna de agua ($p$), que es:
| $ p_t = p_0 + \rho_w g h $ |
Esto nos da:
$\Delta p=p_2-p_1=p_0+\rho_wh_2g-p_0-\rho_wh_1g=\rho_w(h_2-h_1)g$
Dado que la diferencia de altura ($\Delta h$) es:
| $ \Delta h = h_2 - h_1 $ |
la diferencia de presión ($\Delta p$) se puede expresar como:
| $ \Delta p = \rho_w g \Delta h $ |
(ID 4345)
El flujo se define como el volumen el elemento de volumen ($\Delta V$) dividido por el tiempo el tiempo transcurrido ($\Delta t$), lo cual se expresa en la siguiente ecuaci n:
| $ J_V =\displaystyle\frac{ \Delta V }{ \Delta t }$ |
y el volumen es el producto de la secci n la sección del tubo ($S$) por el desplazamiento el elemento del tubo ($\Delta s$):
| $ \Delta V = S \Delta s $ |
Dado que el desplazamiento el elemento del tubo ($\Delta s$) dividido por el tiempo el tiempo transcurrido ($\Delta t$) equivale a la velocidad, se representa con:
| $ j_s =\displaystyle\frac{ \Delta s }{ \Delta t }$ |
Por lo tanto, el flujo es una densidad de flujo ($j_s$), que se calcula mediante:
| $ j_s = \displaystyle\frac{ J_V }{ S }$ |
(ID 4349)
La soluci n original de S.E. Haaland es la siguiente:
$\displaystyle\frac{1}{\sqrt{f_D}}=-1.8\log\left(\left(\displaystyle\frac{\epsilon/R_H}{12}\right)^{1.11} + \displaystyle\frac{6.9}{Re}\right)$
Puede resolverse para obtener la expresi n del factor de fricci n $f_D$ de la siguiente manera:
| $ f_D = \displaystyle\frac{25}{81 \log\left(\left(\displaystyle\frac{ \epsilon }{12 R_H }\right)^{1.11} + \displaystyle\frac{6.9}{ Re }\right)^2}$ |
(ID 14534)
La soluci n original de S.E. Haaland es la siguiente:
$\displaystyle\frac{1}{\sqrt{f_D}}=-1.8\log\left(\left(\displaystyle\frac{\epsilon/D_H}{3.7}\right)^{1.11} + \displaystyle\frac{6.9}{Re}\right)$
Puede resolverse para obtener la expresi n del factor de fricci n $f_D$ de la siguiente manera:
| $ f_D = \displaystyle\frac{25}{81 \log\left(\left(\displaystyle\frac{ \epsilon }{3.7 D_H }\right)^{1.11} + \displaystyle\frac{6.9}{ Re }\right)^2}$ |
(ID 14535)
La sección o superficie ($S$) del tubo que contiene el l quido se puede expresar como una funci n de la profundidad en un tubo no lleno ($h$) integrando sobre el radio hasta el radio del tubo ($R$):
$S = 2\displaystyle\int_0^h dz \sqrt{2Rz - z^2}=\displaystyle\frac{1}{2}(R-h)\sqrt{2Rh - h^2}+\displaystyle\frac{1}{2}R^2\arcsin\left(\displaystyle\frac{1-h}{R}\right)$
Si desarrollamos esta expresi n en t rminos del factor $h/R$ en el l mite $h\ll R$, obtenemos en primer orden:
$S = \sqrt{\displaystyle\frac{2^3}{3^2} R h ^3}$
Si resolvemos para la profundidad, obtenemos finalmente:
| $ h = \left(\displaystyle\frac{3^2 S^2 }{2^3 R }\right)^{1/3}$ |
(ID 14541)
Dado que el ngulo entre el radio en el borde de la superficie del l quido y la vertical se puede calcular con la profundidad en un tubo no lleno ($h$) y el radio del tubo ($R$) mediante:
$\phi =\arccos\left(1-\displaystyle\frac{h}{R}\right)$
El arco correspondiente es $R\phi$, por lo tanto, el arco total es:
$2 R \arccos\left(1-\displaystyle\frac{h}{R}\right)$
De manera an loga, la mitad de la superficie se puede determinar utilizando el teorema de Pit goras, lo que resulta en:
$\sqrt{2Rh - h^2}$
Por lo tanto, el perímetro hidrodinamico ($P_H$) se expresa como:
$P_H = 2\sqrt{2Rh - h^2}+2R\arcsin\left(1-\displaystyle\frac{h}{R}\right)$
En el l mite de una altura peque a, donde $h\ll R$, esta expresi n se puede desarrollar, resultando en:
| $ P_H = \sqrt{2^5 R h }$ |
(ID 14542)
Ejemplos
Cuando se modela el flujo en un tubo, bajo la suposici n de que la densidad de energ a se conserva, se obtiene la ecuaci n de Bernoulli. Esta ecuaci n describe el flujo mediante la diferencia de presión ($\Delta p$) en t rminos de la densidad del líquido ($\rho_w$), la velocidad media del fluido ($v$) y la diferencia de velocidad entre superficies ($\Delta v$):
| $ \Delta p = - \rho \bar{v} \Delta v $ |
En el caso de flujo turbulento, el proceso de mezclado act a como una fricci n que reduce el gradiente de velocidad presente en el flujo laminar entre el centro y las paredes del conducto. Si asumimos que este proceso de mezclado puede ser modelado con un simple factor de correcci n, llegamos emp ricamente a la ecuaci n de Darcy-Weisbach, que involucra el factor de fricción de Darcy-Weisbach ($f_D$), el largo de tubo ($\Delta L$) y la diámetro hidrodinámico ($D_H$):
| $ \Delta p = \displaystyle\frac{ \Delta L }{ D_H } f_D \displaystyle\frac{1}{2} \rho_w j_s ^2 $ |
El factor el factor de fricción de Darcy-Weisbach ($f_D$) ha sido determinado de forma emp rica para diversas condiciones de flujo y se expresa en funci n de el número de Reynold ($Re$).
(ID 15893)
En 1944, Lewis Ferry Moody realiz mediciones del factor de fricci n de Darcy-Weisbach en funci n del n mero de Reynolds y de la rugosidad relativa de la pared, lo que result en la creaci n del siguiente diagrama:

La rugosidad relativa se puede estimar considerando el tama o de las rugosidades (altura de elementos que sobresalen o profundidades de hendiduras) en relaci n con el di metro hidrodin mico.
Se observan dos comportamientos distintos:
• Para n meros de Reynolds inferiores a 2000, el factor de fricci n de Darcy-Weisbach depende solo del n mero de Reynolds, siguiendo una relaci n de $64/Re$. Esto corresponde al r gimen laminar.
• Para n meros de Reynolds superiores a 2000, se observa un comportamiento que depende tanto del n mero de Reynolds como de la rugosidad relativa de la superficie del tubo.
(ID 14528)
En el contexto de la ecuaci n de Darcy-Weisbach, se utiliza una diámetro hidrodinámico ($D_H$), que representa una generalizaci n del di metro tradicional de un c rculo. Esto permite considerar una secci n que no sea circular y calcular un di metro equivalente basado en el rea de la sección del tubo ($S$) y su el perímetro ($P$) mediante la siguiente f rmula:
| $ D_H = \displaystyle\frac{ 4 S }{ P }$ |
Para una secci n circular, recuperamos el di metro tradicional de un c rculo de la siguiente manera:
$D_H = \displaystyle\frac{4 S}{P} = \displaystyle\frac{4 \pi R^2}{2 \pi R} = 2R$
(ID 15894)
En el contexto del factor de fricci n de Darcy-Weisbach, se utiliza un radio hidráulico ($R_H$), que es una generalizaci n del radio tradicional de un c rculo. De esta forma, es posible calcular un di metro basado en el rea de la sección del tubo ($S$) y su per metro en contacto con el perímetro hidrodinamico ($P_H$), utilizando la siguiente f rmula:
| $ R_H = \displaystyle\frac{ S }{ P_H }$ |
Para una secci n circular, podemos obtener el radio hidr ulico tradicional de un c rculo de la siguiente manera:
$R_H = \displaystyle\frac{S}{P} = \displaystyle\frac{\pi R^2}{2 \pi R} = \displaystyle\frac{1}{2} R$
(ID 15895)
En un tubo cil ndrico, la profundidad est relacionada con el flujo de la siguiente manera:

Si integramos la sección o superficie ($S$), podemos calcular c mo var a la superficie en funci n de la profundidad en un tubo no lleno ($h$) mediante la integral sobre el radio hasta el radio del tubo ($R$), lo que resulta en:
$S = 2\displaystyle\int_0^h dz \sqrt{2Rz - z^2}=\displaystyle\frac{1}{2}(R-h)\sqrt{2Rh - h^2}+\displaystyle\frac{1}{2}R^2\arcsin\left(\displaystyle\frac{1-h}{R}\right)$
Para flujos peque os, donde la profundidad es significativamente menor que el radio, la relaci n entre la secci n y la profundidad se simplifica considerablemente. Al resolver la ecuaci n de profundidad, obtenemos:
| $ h = \left(\displaystyle\frac{3^2 S^2 }{2^3 R }\right)^{1/3}$ |
(ID 15896)
El perímetro hidrodinamico ($P_H$) en un tubo parcialmente lleno corresponde a los bordes de la secci n que est n en contacto con el l quido, es decir, el arco que toca la pared del tubo y la superficie:

De esta manera, podemos expresarlo en funci n de el radio del tubo ($R$) y la profundidad en un tubo no lleno ($h$) como:
$P_H = 2 R \arccos\left(1-\displaystyle\frac{h}{R}\right) + 2\sqrt{2Rh-h^2}$
Para flujos peque os, donde la profundidad es considerablemente menor que el radio, esta relaci n se simplifica y establece una conexi n m s directa entre la secci n transversal y la profundidad:
| $ P_H = \sqrt{2^5 R h }$ |
(ID 15897)
Si reemplazamos el factor de fricci n de Darcy-Weisbach en el l mite laminar, dado por
| $ f_D = \displaystyle\frac{64}{ Re }$ |
en la ecuaci n de Darcy-Weisbach, expresada como
| $ \Delta p = \displaystyle\frac{ \Delta L }{ D_H } f_D \displaystyle\frac{1}{2} \rho_w j_s ^2 $ |
y utilizamos la definici n del n mero de Reynolds $Re$, podemos demostrar que el flujo est gobernado por
| $ J_V =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
que corresponde a la ecuaci n de Hagen-Poiseuille.
(ID 14530)
La ecuaci n de Darcy-Weisbach permite calcular la diferencia de presión ($\Delta p$) en funci n de la densidad del líquido ($\rho_w$), la diámetro hidrodinámico ($D_H$), el factor de fricción de Darcy-Weisbach ($f_D$), el largo de tubo ($\Delta L$) y la velocidad media del fluido ($v$) a trav s de:
| $ \Delta p = \displaystyle\frac{ \Delta L }{ D_H } f_D \displaystyle\frac{1}{2} \rho_w j_s ^2 $ |
(ID 14526)
Se puede representar una densidad de flujo ($j_s$) en t rminos de el flujo de volumen ($J_V$) utilizando la sección o superficie ($S$) mediante la siguiente f rmula:
| $ j_s = \displaystyle\frac{ J_V }{ S }$ |
(ID 4349)
La diámetro hidrodinámico ($D_H$) se puede calcular a partir de la sección del tubo ($S$) y el perímetro ($P$) mediante:
| $ D_H = \displaystyle\frac{ 4 S }{ P }$ |
(ID 14527)
El radio hidráulico ($R_H$) se puede calcular a partir de la sección del tubo ($S$) y el perímetro hidrodinamico ($P_H$) mediante:
| $ R_H = \displaystyle\frac{ S }{ P_H }$ |
(ID 14531)
La profundidad en un tubo no lleno ($h$) se puede estimar cuando el nivel del l quido es bajo, es decir, cuando dicho nivel es mucho menor que el radio del tubo, en funci n de la sección o superficie ($S$) y el radio del tubo ($R$):
| $ h = \left(\displaystyle\frac{3^2 S^2 }{2^3 R }\right)^{1/3}$ |
(ID 14541)
El perímetro hidrodinamico ($P_H$) se puede estimar a partir de la profundidad en un tubo no lleno ($h$) y el radio del tubo ($R$) mediante:
| $ P_H = \sqrt{2^5 R h }$ |
(ID 14542)
El criterio clave para determinar si un medio es laminar o turbulento es el llamado numero de Reynold que compara la energ a asociada a la inercia con aquella asociada a la viscosiadad. La primera depende de la densidad ($\rho$), la velocidad media del fluido ($v$) y la dimensión típica del sistema ($R$) mientras que la segunda de la viscosidad ($\eta$) con lo que se define:
| $ Re =\displaystyle\frac{ \rho R v }{ \eta }$ |
(ID 3177)
En el l mite de bajos el número de Reynold ($Re$), el diagrama de Moody muestra que el factor de fricción de Darcy-Weisbach ($f_D$) es igual a:
| $ f_D = \displaystyle\frac{64}{ Re }$ |
donde $Re$ es el n mero de Reynolds. Esto es v lido para n meros de Reynolds hasta 2000. M s all de este valor, la rugosidad de la pared comienza a influir en la destabilizaci n del flujo y en la formaci n de turbulencias.
(ID 14529)
La ecuaci n de Colebrook-White para el caso de un tubo cerrado:
| $\displaystyle\frac{1}{\sqrt{ f_D }}=-2\log\left(\displaystyle\frac{\epsilon}{3.7 D_H}+\displaystyle\frac{2.51}{ Re \sqrt{ f_D }}\right)$ |
es una ecuaci n impl cita utilizada para determinar el factor de fricci n de Darcy-Weisbach ($f_D$). Para resolver esta ecuaci n, se han desarrollado diversas aproximaciones que var an en complejidad y precisi n. Una de las aproximaciones m s efectivas, que abarca un amplio rango de n meros de Reynolds $Re$, es la propuesta por S.E. Haaland:
| $ f_D = \displaystyle\frac{25}{81 \log\left(\left(\displaystyle\frac{ \epsilon }{3.7 D_H }\right)^{1.11} + \displaystyle\frac{6.9}{ Re }\right)^2}$ |
(ID 14535)
La ecuaci n de Colebrook-White para el caso de un tubo cerrado:
| $\displaystyle\frac{1}{\sqrt{ f_D }}=-2\log\left(\displaystyle\frac{\epsilon}{12 R_H}+\displaystyle\frac{2.51}{ Re \sqrt{ f_D }}\right)$ |
es una ecuaci n impl cita utilizada para determinar el factor de fricci n de Darcy-Weisbach ($f_D$). Para resolver esta ecuaci n, se han desarrollado diversas aproximaciones que var an en complejidad y precisi n. Una de las aproximaciones m s efectivas, que abarca un amplio rango de n meros de Reynolds $Re$, es la propuesta por S.E. Haaland:
| $ f_D = \displaystyle\frac{25}{81 \log\left(\left(\displaystyle\frac{ \epsilon }{12 R_H }\right)^{1.11} + \displaystyle\frac{6.9}{ Re }\right)^2}$ |
(ID 14534)
La diferencia de alturas, representada por la diferencia de altura ($\Delta h$), implica que la presi n en ambas columnas es diferente. En particular, la diferencia de presión ($\Delta p$) es una funci n de la densidad del líquido ($\rho_w$), la aceleración gravitacional ($g$) y la diferencia de altura ($\Delta h$), de la siguiente manera:
| $ \Delta p = \rho_w g \Delta h $ |
(ID 4345)
La ecuaci n de Darcy-Weisbach permite calcular la diferencia de presión ($\Delta p$) en funci n de la densidad del líquido ($\rho_w$), la diámetro hidrodinámico ($D_H$), el factor de fricción de Darcy-Weisbach ($f_D$), el largo de tubo ($\Delta L$) y la velocidad media del fluido ($v$) a trav s de:
| $ \Delta h_d = \displaystyle\frac{ \Delta L }{ 2 g D_H } f_D j_s ^2 $ |
(ID 15958)
ID:(1970, 0)
