Utilisateur:
Écoulement turbulent à travers des tubes
Storyboard
Si le nombre de Reynolds dépasse 2000, l'écoulement dans un tube devient toujours instable et finit par devenir complètement turbulent. Par conséquent, il n'est plus possible d'utiliser l'approximation d'écoulement visqueux laminaire qui donne lieu à la loi de Hagen-Poiseuille, et un modèle alternatif est nécessaire.
Le modèle qui décrit un écoulement où la viscosité est négligeable est celui qui donne naissance à l'équation de Bernoulli. Cependant, ce modèle suppose que la densité d'énergie soit conservée. Une alternative consiste à supposer que les turbulences conduisent à un mélange de telle manière que la densité d'énergie ne soit pas conservée mais reste constante. Dans ce cas, l'écoulement peut être modélisé à l'aide d'une équation similaire à celle de Bernoulli, mais avec une correction pour prendre en compte l'homogénéisation due aux effets de mélange.
ID:(1970, 0)
Modélisation des turbulences
Image
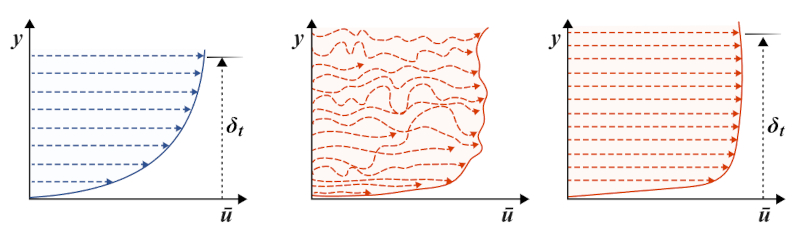
L'écoulement laminaire est décrit par des "feuilles" qui se déplacent à différentes vitesses de manière coordonnée. En revanche, dans l'écoulement turbulent, ces "feuilles" n'existent pas. Les éléments du fluide sont déviés, peuvent changer de direction et participer à des mouvements circulaires, souvent de manière chaotique.
La première conséquence de cela est que les paramètres du fluide ont tendance à se mélanger, provoquant la disparition des différences de vitesse et l'émergence d'un type de vitesse moyenne. En moyennant le mouvement, des motifs structurés émergent, mais ils ne proviennent plus des éléments individuels du fluide, mais plutôt d'un mélange temporel. En conséquence, un profil relativement constant similaire aux profils définis dans l'écoulement laminaire émerge à nouveau, mais dans ce cas, ce sont des valeurs moyennes et présentant moins de grands gradients, les rendant plus uniformes.
ID:(14525, 0)
Équation de Darcy-Weisbach
Équation
Lorsque l'on modélise l'écoulement dans un tube en supposant que la densité d'énergie est conservée, nous obtenons l'équation de Bernoulli, qui décrit dans ce cas l'écoulement de la manière suivante :
| $ \Delta p = - \rho \bar{v} \Delta v $ |
où $\Delta p$ est la différence de pression, $\rho$ est la densité et $v$ est la vitesse.
Dans le cas de l'écoulement turbulent, le processus de mélange agit comme une friction, réduisant le gradient de vitesse qui existe dans l'écoulement laminaire entre le centre et le bord de l'écoulement. En supposant que ce facteur de mélange peut être modélisé empiriquement avec un facteur de correction, nous obtenons empiriquement l'équation de Darcy-Weisbach :
 $ \Delta p = \displaystyle\frac{ \Delta L }{ D_H } f_D \displaystyle\frac{1}{2} \rho_w v ^2 $ |
où $f_D$ est le facteur de friction de Darcy, $\Delta L$ est la longueur et $D_H$ est le diamètre hydraulique du tube.
Le facteur de friction a été déterminé de manière empirique pour diverses situations et est exprimé en fonction du nombre de Reynolds.
ID:(14526, 0)
Diamètre hydraulique
Équation
Dans le cas de l'équation de Darcy-Weisbach, nous travaillons avec un diamètre hydraulique qui correspond à une généralisation du diamètre traditionnel d'un cercle. Cela nous permet de prendre en compte une section non circulaire et de calculer un diamètre en fonction de la surface de la section, notée $S$, et de son périmètre, noté $P$, en utilisant la formule suivante :
| $ D_H = \displaystyle\frac{ 4 S }{ P }$ |
Dans le cas d'une section circulaire, nous obtenons le diamètre traditionnel d'un cercle de la manière suivante :
$D_H = \displaystyle\frac{4S}{P} = \displaystyle\frac{4\pi R^2}{2\pi R} = 2R$
ID:(14527, 0)
Rayon hydraulique
Équation
Dans le contexte du facteur de frottement de Darcy-Weisbach, nous travaillons avec un rayon hydraulique qui correspond à une généralisation du rayon traditionnel d'un cercle. Cela nous permet de calculer un diamètre en fonction de la surface de la section transversale $S$ et de son périmètre en contact avec le liquide $P$, en utilisant la formule suivante :
| $ R_H = \displaystyle\frac{ S }{ P_H }$ |
Lorsqu'il s'agit d'une section circulaire, nous obtenons le rayon hydraulique traditionnel d'un cercle de la manière suivante :
$R_H = \displaystyle\frac{S}{P} = \displaystyle\frac{\pi R^2}{2 \pi R} = \displaystyle\frac{1}{2} R$
ID:(14531, 0)
Profondeur d'un tube non rempli
Équation
Dans un tube cylindrique, la profondeur dépend du flux de la manière suivante :
Si nous intégrons la section transversale, nous pouvons calculer comment la surface dépend de la profondeur en utilisant l'équation suivante :
$S = 2\displaystyle\int_0^h dz \sqrt{2Rz - z^2}=\displaystyle\frac{1}{2}(R-h)\sqrt{2Rh - h^2}+\displaystyle\frac{1}{2}R^2\arcsin\left(\displaystyle\frac{1-h}{R}\right)$
Pour de faibles débits, où la profondeur est nettement inférieure au rayon, la relation entre la section et la profondeur se simplifie considérablement. En résolvant pour la profondeur, nous obtenons:
| $ h = \left(\displaystyle\frac{3^2 S^2 }{2^3 R }\right)^{1/3}$ |
La section transversale du tube contenant le liquide peut être intégrée par rapport à la hauteur de la manière suivante :
$S = 2\displaystyle\int_0^h dz \sqrt{2Rz - z^2}=\displaystyle\frac{1}{2}(R-h)\sqrt{2Rh - h^2}+\displaystyle\frac{1}{2}R^2\arcsin\left(\displaystyle\frac{1-h}{R}\right)$
Si nous développons cette expression en fonction du facteur $h/R$ dans la limite $h\ll R$, nous obtenons, au premier ordre :
$S = \sqrt{\displaystyle\frac{2^3}{3^2} R h ^3}$
Si nous résolvons pour la profondeur, nous obtenons finalement:
| $ h = \left(\displaystyle\frac{3^2 S^2 }{2^3 R }\right)^{1/3}$ |
ID:(14541, 0)
Périmètre hydrodynamique en tube non rempli
Équation
Le périmètre hydrodynamique d'un tube partiellement rempli correspond aux bords de la section en contact avec le liquide, à savoir l'arc touchant la paroi du tube et la surface :
En général, cela peut être exprimé comme suit :
$P_H = 2 R \arccos\left(1-\displaystyle\frac{h}{R}\right) + 2\sqrt{2Rh-h^2}$
Pour de faibles débits, où la profondeur est nettement inférieure au rayon, cela simplifie la relation entre la section et la profondeur à :
| $ P_H = \sqrt{2^5 R h }$ |
Étant donné que l'angle peut être déterminé comme suit:
$\phi =\arccos\left(1-\displaystyle\frac{h}{R}\right)$
L'arc est égal à $R\phi$, par conséquent, la longueur totale de l'arc est:
$2 R \arccos\left(1-\displaystyle\frac{h}{R}\right)$
De manière similaire, la moitié de la surface peut être déterminée en utilisant le théorème de Pythagore, ce qui donne:
$\sqrt{2Rh - h^2}$
Ainsi, le périmètre hydrodynamique s'exprime comme suit:
$S = 2\displaystyle\int_0^h dz \sqrt{2Rz - z^2}=\displaystyle\frac{1}{2}(R-h)\sqrt{2Rh - h^2}+\displaystyle\frac{1}{2}R^2\arcsin\left(1-\displaystyle\frac{h}{R}\right)$
Dans la limite d'une petite hauteur, où $h\ll R$, cette expression peut être développée, donnant:
| $ P_H = \sqrt{2^5 R h }$ |
ID:(14542, 0)
Diagramme de Moody
Image
En 1944, Lewis Ferry Moody a mesuré le facteur de frottement de Darcy-Weisbach en fonction du nombre de Reynolds et de la rugosité relative de la paroi, ce qui a conduit à la création du diagramme suivant :
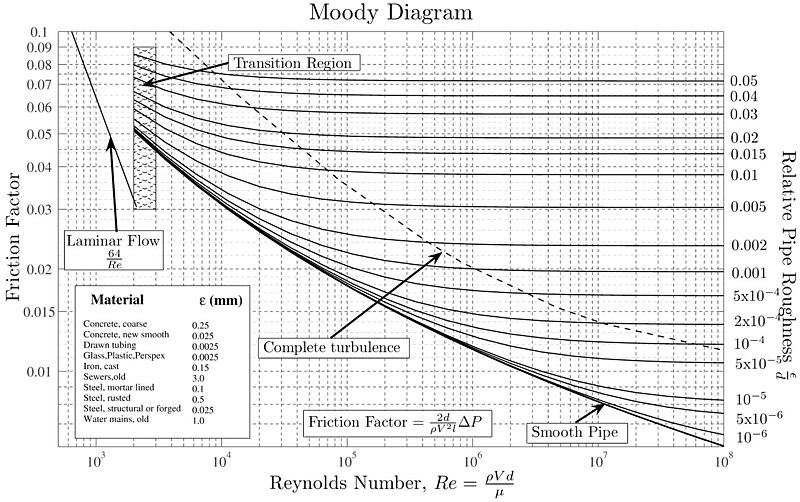
La rugosité relative peut être estimée en considérant la taille des irrégularités de surface (hauteur des saillies ou profondeur des rainures) par rapport au diamètre hydraulique.
Deux comportements distincts sont observés :
• Pour des nombres de Reynolds inférieurs à 2000, le facteur de frottement de Darcy-Weisbach dépend uniquement du nombre de Reynolds, suivant une relation de $64/Re$. Cela correspond au régime d'écoulement laminaire.
• Pour des nombres de Reynolds supérieurs à 2000, un comportement est observé qui dépend à la fois du nombre de Reynolds et de la rugosité relative de la surface du tube.
ID:(14528, 0)
Limite laminaire
Équation
À de faibles nombres de Reynolds, le diagramme de Moody montre que le facteur de frottement de Darcy-Weisbach, $f_D$, est égal à :
| $ f_D = \displaystyle\frac{64}{ Re }$ |
où $Re$ est le nombre de Reynolds. Ceci s'applique pour les nombres de Reynolds jusqu'à 2000. Au-delà de cette valeur, la rugosité de la paroi commence à influencer la déstabilisation de l'écoulement et la formation de turbulences.
ID:(14529, 0)
Écoulement à la limite laminaire
Description
Si nous remplaçons le facteur de frottement de Darcy-Weisbach dans la limite laminaire, donné par
| $ f_D = \displaystyle\frac{64}{ Re }$ |
dans l'équation de Darcy-Weisbach, exprimée comme
| $ \Delta p = \displaystyle\frac{ \Delta L }{ D_H } f_D \displaystyle\frac{1}{2} \rho_w v ^2 $ |
et utilisons la définition du nombre de Reynolds $Re$, nous pouvons démontrer que l'écoulement est régi par
| $ J_V =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
ce qui correspond à l'équation de Hagen-Poiseuille.
ID:(14530, 0)
Équation de Colebrook-White en tube fermé
Équation
Dans le cas où le tube est complètement fermé, c'est-à-dire que le cylindre n'a pas d'ouverture supérieure et que le liquide remplit toute la section, l'équation de Colebrook-White
| $\displaystyle\frac{1}{\sqrt{ f_D }}=-2\log\left(\displaystyle\frac{\epsilon}{3.7 D_H}+\displaystyle\frac{2.51}{ Re \sqrt{ f_D }}\right)$ |
permet d'estimer le facteur de frottement de Darcy-Weisbach en cas d'écoulement turbulent en fonction de la rugosité $\epsilon$, du diamètre hydraulique et du nombre de Reynolds.
ID:(14532, 0)
Solution pour tube fermé
Équation
L'équation de Colebrook-White pour le cas d'un tube fermé :
| $\displaystyle\frac{1}{\sqrt{ f_D }}=-2\log\left(\displaystyle\frac{\epsilon}{3.7 D_H}+\displaystyle\frac{2.51}{ Re \sqrt{ f_D }}\right)$ |
est une équation implicite utilisée pour déterminer le coefficient de friction de Darcy-Weisbach ($f_D$). Pour résoudre cette équation, plusieurs approximations ont été développées, variant en termes de complexité et de précision. L'une des approximations les plus efficaces couvrant une large gamme de nombres de Reynolds $Re$ est celle proposée par S.E. Haaland :
| $ f_D = \displaystyle\frac{25}{81 \log\left(\left(\displaystyle\frac{ \epsilon }{3.7 D_H }\right)^{1.11} + \displaystyle\frac{6.9}{ Re }\right)^2}$ |
La solution originale de S.E. Haaland est la suivante:
$\displaystyle\frac{1}{\sqrt{f_D}}=-1.8\log\left(\left(\displaystyle\frac{\epsilon/D_H}{3.7}\right)^{1.11} + \displaystyle\frac{6.9}{Re}\right)$
Elle peut être réorganisée pour obtenir l'expression du facteur de friction de Darcy-Weisbach $f_D$ comme suit :
| $ f_D = \displaystyle\frac{25}{81 \log\left(\left(\displaystyle\frac{ \epsilon }{3.7 D_H }\right)^{1.11} + \displaystyle\frac{6.9}{ Re }\right)^2}$ |
ID:(14535, 0)
Équation de Colebrook-White en tube ouvert
Équation
Lorsque le tube est ouvert, c'est-à-dire lorsque le liquide ne remplit pas toute la section du cylindre, l'équation de Colebrook-White
| $\displaystyle\frac{1}{\sqrt{ f_D }}=-2\log\left(\displaystyle\frac{\epsilon}{12 R_H}+\displaystyle\frac{2.51}{ Re \sqrt{ f_D }}\right)$ |
permet d'estimer le facteur de frottement de Darcy-Weisbach en cas d'écoulement turbulent en fonction de la rugosité $\epsilon$, du diamètre hydraulique et du nombre de Reynolds.
ID:(14533, 0)
Solution pour tube ouvert
Équation
L'équation de Colebrook-White pour le cas d'un tube fermé :
| $\displaystyle\frac{1}{\sqrt{ f_D }}=-2\log\left(\displaystyle\frac{\epsilon}{12 R_H}+\displaystyle\frac{2.51}{ Re \sqrt{ f_D }}\right)$ |
est une équation implicite utilisée pour déterminer le coefficient de friction de Darcy-Weisbach ($f_D$). Pour résoudre cette équation, plusieurs approximations ont été développées, variant en termes de complexité et de précision. L'une des approximations les plus efficaces couvrant une large gamme de nombres de Reynolds $Re$ est celle proposée par S.E. Haaland :
| $ f_D = \displaystyle\frac{25}{81 \log\left(\left(\displaystyle\frac{ \epsilon }{12 R_H }\right)^{1.11} + \displaystyle\frac{6.9}{ Re }\right)^2}$ |
La solution originale de S.E. Haaland est la suivante:
$\displaystyle\frac{1}{\sqrt{f_D}}=-1.8\log\left(\left(\displaystyle\frac{\epsilon/R_H}{12}\right)^{1.11} + \displaystyle\frac{6.9}{Re}\right)$
Elle peut être réorganisée pour obtenir l'expression du facteur de friction de Darcy-Weisbach $f_D$ comme suit :
| $ f_D = \displaystyle\frac{25}{81 \log\left(\left(\displaystyle\frac{ \epsilon }{12 R_H }\right)^{1.11} + \displaystyle\frac{6.9}{ Re }\right)^2}$ |
ID:(14534, 0)
Profil de vitesse d'écoulement turbulent dans le tube
Image
Le profil de vitesse de l'écoulement turbulent à travers un tube présente deux zones distinctes en fonction de la distance à la surface ($z$), où $\delta$ représente l'épaisseur de la couche limite. Dans la région proche de la surface ($z < \delta$), l'écoulement est essentiellement laminaire, tandis que dans la région plus éloignée de la surface ($z > \delta$), l'écoulement devient turbulent.
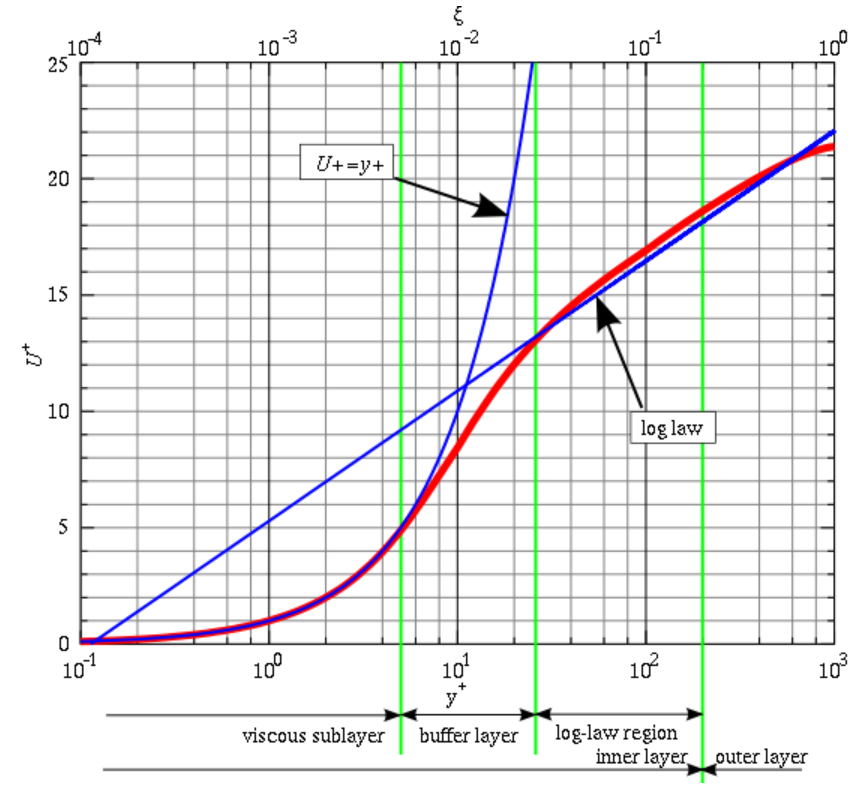
Dans la plage laminaire, la vitesse est proportionnelle à la distance normalisée :
$u^+ = y^+$
Cette relation est similaire au profil de vitesse de Hagen-Poiseuille près de la paroi et représente une approximation linéaire.
Dans la plage turbulente, le profil de vitesse normalisée prend une forme logarithmique :
$u^+ = \displaystyle\frac{1}{\kappa} \ln\left(\displaystyle\frac{y^+}{y_0}\right)$
Ici, $\kappa$ est la constante de Karman (environ $0,41$), et $y_0\sim 1/8$ est la distance normalisée à laquelle la vitesse serait nulle. Cependant, il est important de noter que la largeur de la couche laminée, comme indiqué sur le graphique, est d'environ 7,072 fois plus grande que $y_0$.
ID:(14536, 0)
Vitesse de coupe
Équation
À l'intérieur de la couche limite laminaire, le profil de vitesse est donné par
| $ v = v_{max} \left(1-\displaystyle\frac{ r ^2}{ R ^2}\right)$ |
ce qui, dans la limite des distances proches de la paroi ($r \sim R$), nous permet de définir la distance adimensionnelle
$y^+=\displaystyle\frac{\rho_w u_{\tau}}{\eta} y$
et la vitesse adimensionnelle
$u^+=\displaystyle\frac{u}{u_{\tau}}$
En normalisant ces valeurs, nous obtenons la loi logarithmique de la vitesse turbulente
| $ u_{\tau} =\sqrt{\displaystyle\frac{ R }{2 \rho_w }\displaystyle\frac{ \Delta p }{ \Delta L }}$ |
Dans l'écoulement laminaire, selon Hagen-Poiseuille, le profil de vitesse est défini comme suit:
| $ v = v_{max} \left(1-\displaystyle\frac{ r ^2}{ R ^2}\right)$ |
avec l'équation supplémentaire:
| $ v_{max} =-\displaystyle\frac{ R ^2}{4 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
Cela nous fournit une relation pour la vitesse en fonction de la distance par rapport à la paroi :
$v=v_{max}\displaystyle\frac{2y}{R}=\displaystyle\frac{R}{2\eta}\displaystyle\frac{\Delta p}{\Delta L}y$
qui correspond à la relation normalisée :
$u^+=y^+$
Lorsque l'on considère la vitesse de cisaillement $u_{\tau}$, la vitesse normalisée s'exprime comme suit:
$u^+=\displaystyle\frac{v}{u_{\tau}}$
et la distance à la paroi normalisée est:
$y^+=\displaystyle\frac{\rho_w u_{\tau}}{\eta} y$
Ainsi, nous obtenons:
$u^+=\displaystyle\frac{v}{u_{\tau}}=\displaystyle\frac{R\Delta p}{2\eta\Delta L u_{\tau}}y=y^+=\displaystyle\frac{\rho_w u_{\tau}}{\eta}y$
ce qui nous conduit à:
| $ u_{\tau} =\sqrt{\displaystyle\frac{ R }{2 \rho_w }\displaystyle\frac{ \Delta p }{ \Delta L }}$ |
ID:(14538, 0)
Équation du profil de vitesse d'écoulement turbulent
Équation
De manière empirique, il a été déterminé que la vitesse dans l'écoulement turbulent à l'intérieur d'un tube suit la forme suivante :
$u^+ = \displaystyle\frac{1}{\kappa} \ln\left(\displaystyle\frac{y^+}{y_0}\right)$
En utilisant la vitesse de cisaillement
| $ u_{\tau} =\sqrt{\displaystyle\frac{ R }{2 \rho_w }\displaystyle\frac{ \Delta p }{ \Delta L }}$ |
nous pouvons décrire la vitesse dans l'écoulement turbulent à travers un tube comme suit :
| $ v_y = \displaystyle\frac{ u_{\tau} }{ \kappa }\ln\left(\displaystyle\frac{8 \rho_w u_{\tau} y }{ \eta }\right)$ |
De manière empirique, il a été déterminé que la vitesse dans l'écoulement turbulent à l'intérieur d'un tube suit la forme suivante :
$u^+ = \displaystyle\frac{1}{\kappa} \ln\left(\displaystyle\frac{y^+}{y_0}\right)$
Où la vitesse normalisée est donnée par :
$u^+=\displaystyle\frac{v}{u_{\tau}}$
Et la distance normalisée par rapport à la paroi est définie comme :
$y^+=\displaystyle\frac{\rho_w u_{\tau}}{\eta}y$
Avec la vitesse de cisaillement fournie par :
| $ u_{\tau} =\sqrt{\displaystyle\frac{ R }{2 \rho_w }\displaystyle\frac{ \Delta p }{ \Delta L }}$ |
Cela nous conduit à obtenir :
| $ v_y = \displaystyle\frac{ u_{\tau} }{ \kappa }\ln\left(\displaystyle\frac{8 \rho_w u_{\tau} y }{ \eta }\right)$ |
où l'on suppose que $y_0 \sim 1/8.
ID:(14537, 0)
Épaisseur de la couche d'écoulement laminaire
Équation
L'épaisseur de la couche limite laminaire peut être définie en fonction de la condition selon laquelle les profils de vitesse laminaires correspondent au profil logarithmique correspondant à l'écoulement turbulent. Cela se produit lorsque
$y^+=u^+=\displaystyle\frac{1}{\kappa}\ln\left(\displaystyle\frac{y^+}{y_0}\right)$
dont la racine est $7.072$. Étant donné qu'il s'agit d'une estimation de l'épaisseur, et que la normalisation inclut un facteur de $1/8$, les chiffres peuvent être simplifiés au premier ordre, et l'épaisseur peut être estimée comme suit :
| $ \delta = \displaystyle\frac{ \eta }{ \rho_w u_{\tau} }$ |
Dans la couche laminée, l'écoulement a la forme
$u^+ = y^+$
tandis que dans la région turbulente, il est
$u^+=\displaystyle\frac{1}{\kappa}\ln\left(\displaystyle\frac{y^+}{y_0}\right)$
En égalant ces deux fonctions pour définir la frontière, nous obtenons l'équation
$y^+=\displaystyle\frac{1}{\kappa}\ln\left(\displaystyle\frac{y^+}{y_0}\right)$
dont la solution numérique est
$y^+=7.072 \text{ et } y_0=\displaystyle\frac{7.072}{8}\sim 1$
où la valeur empirique pour $y_0=1/8$ a été utilisée, et étant donné qu'il s'agit d'une estimation, nous supposons que $7/8\sim 1$.
Avec la définition de la normalisation
$y^+=\displaystyle\frac{\rho_w u_{\tau}}{\eta} y = 1$
et en résolvant pour $y$, nous obtenons
| $ \delta = \displaystyle\frac{ \eta }{ \rho_w u_{\tau} }$ |
ID:(14539, 0)
Contrainte de cisaillement sur les murs
Équation
La vitesse de cisaillement, $u_{\tau}$, est directement associée à la contrainte de cisaillement, $\tau_w$, générée par l'écoulement sur les parois du tube :
| $ \tau_w = \rho u_{\tau} ^2$ |
Cela exerce des forces sur les parois et affecte les systèmes qui peuvent bouger, de manière similaire au cas où l'air coule sur l'eau.
ID:(14540, 0)