Hydrostatischer Druck
Storyboard 
Eine Säule aus Flüssigkeit übt aufgrund ihrer Masse eine Kraft auf ihre Basis aus. Da diese Kraft direkt proportional zur Querschnittsfläche ist, ist es sinnvoll, das Konzept der Kraft pro Flächeneinheit einzuführen, das wir als Druck bezeichnen.
Der Druck kann durch die Bewegung der Flüssigkeit beeinflusst werden, und wir unterscheiden zwischen dem allgemeinen Druck und dem hydrostatischen Druck (hydro = Flüssigkeit, statisch = ohne Bewegung).
ID:(874, 0)
Hydrostatischer Druck
Storyboard 
Eine Säule aus Flüssigkeit übt aufgrund ihrer Masse eine Kraft auf ihre Basis aus. Da diese Kraft direkt proportional zur Querschnittsfläche ist, ist es sinnvoll, das Konzept der Kraft pro Flächeneinheit einzuführen, das wir als Druck bezeichnen. Der Druck kann durch die Bewegung der Flüssigkeit beeinflusst werden, und wir unterscheiden zwischen dem allgemeinen Druck und dem hydrostatischen Druck (hydro = Flüssigkeit, statisch = ohne Bewegung).
Variablen
Berechnungen
Berechnungen
Gleichungen
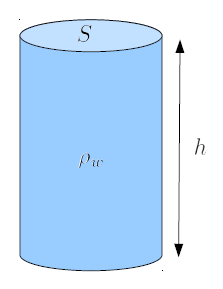
Da die Masse der Flüssigkeitssäule ($M$) gem der Gleichung von die Flüssigkeitsdichte ($\rho_w$), die Column Abschnitt ($S$) und die Höhe der Säule ($h$) abh ngt:
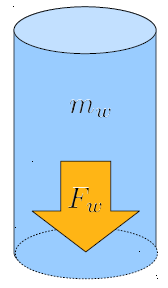
und die Kraft der Säule ($F$) mit die Gravitationsbeschleunigung ($g$) dargestellt wird:
kann der Ausdruck wie folgt geschrieben werden:
Da die die Kraft der Säule ($F$), die von einer Fl ssigkeitss ule von die Höhe der Säule ($h$), die Column Abschnitt ($S$), die Flüssigkeitsdichte ($\rho_w$) und die Gravitationsbeschleunigung ($g$) erzeugt wird, ist
und die die Druck der Wassersäule ($p$) dann definiert ist als
haben wir, dass die von einer Fl ssigkeitss ule erzeugte die Druck der Wassersäule ($p$) ist
Die Masse der Flüssigkeitssäule ($M$) kann aus die Flüssigkeitsdichte ($\rho_w$) und der Säulenvolumen ($V$) berechnet werden.
Um die Flüssigkeitsdichte ($\rho_w$) zu berechnen, wird die folgende Gleichung verwendet:
Und f r der Säulenvolumen ($V$) gilt:
Auf diese Weise wird der Wert von die Masse der Flüssigkeitssäule ($M$) ermittelt durch:
Beispiele
Um das Verhalten von Fl ssigkeiten zu untersuchen, ist es n tzlich, das Konzept einer Fl ssigkeitss ule einzuf hren. Diese S ule ist eine Abstraktion eines zylindrischen Beh lters (wie eines Messzylinders), der Fl ssigkeit enth lt, und erm glicht es uns, die Kraft zu untersuchen, der ein Objekt darin ausgesetzt ist.
Sobald dieses Konzept eingef hrt ist, k nnen wir an seine Existenz unabh ngig vom Beh lter denken, der sie enth lt. Zum Beispiel ist ein Taucher, der im offenen Meer schwimmt, dem Gewicht ausgesetzt, das von einer "imagin ren" Fl ssigkeitss ule erzeugt wird, die ber ihm von der Oberfl che der Fl ssigkeit bis zu seiner Haut und der Oberfl che des Meeres reicht.
die Masse der Flüssigkeitssäule ($M$) kann aus die Flüssigkeitsdichte ($\rho_w$) und der Säulenvolumen ($V$) berechnet werden.
Um die Flüssigkeitsdichte ($\rho_w$) zu berechnen, wird die folgende Gleichung verwendet:
Und f r der Säulenvolumen ($V$) gilt:
Auf diese Weise wird der Wert von die Masse der Flüssigkeitssäule ($M$) ermittelt durch:
Dies ist g ltig, solange die Column Abschnitt ($S$) w hrend die Höhe der Säule ($h$) konstant bleibt.
Der Abschnitt kann sich in seiner Form ndern, aber nicht in seiner Oberfl che.
Sobald das Volumen und somit die Masse der S ule bekannt sind, kann die Kraft berechnet werden, die sie auf ihren Boden aus bt. Es ist wichtig zu beachten, dass dies auf Fl ssigkeiten angewendet wird, die als inkompressibel betrachtet werden, was bedeutet, dass die unteren Schichten der Fl ssigkeit angenommen werden, nicht durch das Gewicht der oberen Schichten komprimiert zu werden.
Dieses Prinzip kann angewendet werden, um die Kraft zu berechnen, die von jeder Fl ssigkeit ausge bt wird, wie z.B. Wasser oder l, und ist besonders n tzlich in der Hydraulik und der Str mungsmechanik.
Da die Masse der Flüssigkeitssäule ($M$) gem der Gleichung von die Flüssigkeitsdichte ($\rho_w$), die Column Abschnitt ($S$) und die Höhe der Säule ($h$) abh ngt:
und die Kraft der Säule ($F$) mit die Gravitationsbeschleunigung ($g$) dargestellt wird:
kann der Ausdruck wie folgt geschrieben werden:
In der Mechanik beschreiben wir, wie K rper mit definierter Masse sich bewegen. Im Fall einer Fl ssigkeit ist die Bewegung nicht gleichm ig, und jeder Abschnitt der Fl ssigkeit bewegt sich unterschiedlich. Diese \\"Abschnitte\\" haben jedoch keine definierte Masse, da sie keine definierten oder getrennten Objekte sind.
Um dieses Problem zu l sen, k nnen wir die Fl ssigkeit in eine Reihe von kleinen, getrennten Volumina segmentieren und, falls m glich, ihre Masse mit Hilfe der Dichte sch tzen. Auf diese Weise k nnen wir die Idee einf hren, dass Kr fte die Bewegung der Fl ssigkeit definieren.
Letztendlich sind Volumina jedoch arbitr r, und was letztlich die Bewegung erzeugt, ist die Kraft, die auf die Fl che des Volumens wirkt. Daher macht es mehr Sinn, das Konzept von ERROR:10113,0 pro solchem ERROR:6002,0 einzuf hren, das als die Druck der Wassersäule ($p$) bezeichnet wird.
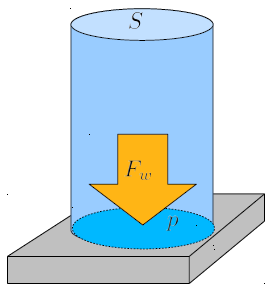
Die auf den Boden wirkende die Kraft der Säule ($F$) h ngt in dem Sinne von die Column Abschnitt ($S$) ab, dass sich die Kraft in derselben Proportion ndert, wenn letzteres variiert. In diesem Sinne sind die Kraft der Säule ($F$) und die Column Abschnitt ($S$) nicht voneinander abh ngig; sie ver ndern sich proportional. Es macht Sinn, diese Proportion als die Druck ($p$) zu definieren:
Da die die Kraft der Säule ($F$), die von einer Fl ssigkeitss ule von die Höhe der Säule ($h$), die Column Abschnitt ($S$), die Flüssigkeitsdichte ($\rho_w$) und die Gravitationsbeschleunigung ($g$) erzeugt wird, ist
und die die Druck der Wassersäule ($p$) dann definiert ist als
haben wir, dass die von einer Fl ssigkeitss ule erzeugte die Druck der Wassersäule ($p$) ist
Dies ist das Gesetz des hydrostatischen Drucks, auch bekannt als Pascalsches Gesetz, das haupts chlich Blaise Pascal zugeschrieben wird [1].
![]() [1] "Trait de l' quilibre des liqueurs" (Abhandlung ber das Gleichgewicht der Fl ssigkeiten), Blaise Pascal, 1663.
[1] "Trait de l' quilibre des liqueurs" (Abhandlung ber das Gleichgewicht der Fl ssigkeiten), Blaise Pascal, 1663.
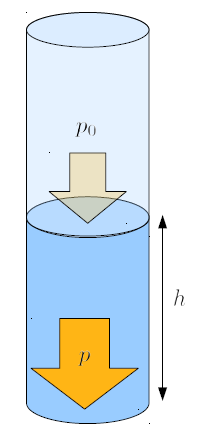
Wenn angenommen wird, dass die S ule von die Atmosphärischer Druck ($p_0$) beeinflusst wird, muss der Beitrag von die Atmosphärischer Druck ($p_0$) zu die Druck der Wassersäule ($p$) der S ule hinzugef gt werden, wie hier gezeigt:
Beim Berechnen von die Druck der Wassersäule ($p$) in einer bestimmten Tiefe ist es wichtig zu ber cksichtigen, dass die Oberfl che der Fl ssigkeit die Atmosphärischer Druck ($p_0$) ausgesetzt ist, was den Druckwert an dieser Stelle beeinflussen kann. Daher ist es notwendig, die Gleichung f r die Druck der Wassersäule ($p$) zu verallgemeinern, um nicht nur die Fl ssigkeitss ule die Flüssigkeitsdichte ($\rho_w$), die Höhe der Säule ($h$) und die Gravitationsbeschleunigung ($g$) einzubeziehen, sondern auch die Atmosphärischer Druck ($p_0$):
Es ist nicht immer notwendig, den Luftdruck in der Modellierung zu ber cksichtigen:
In vielen F llen ist der Luftdruck im gesamten System vorhanden, sodass Druckunterschiede nicht von ihm abh ngen.
Es ist wichtig zu verstehen, dass der Druck nur von der Tiefe abh ngt und es nicht notwendig ist, dass sich direkt ber dem Messpunkt eine Fl ssigkeitss ule befindet. Dies liegt daran, dass jeder Druckunterschied bei gleicher Tiefe zu einem Fluss f hren wird, bis der Druck ausgeglichen ist.
Mit anderen Worten ist der Druck eine skalare Gr e, die nur von der vertikalen Entfernung von der Oberfl che der Fl ssigkeit bis zum Messpunkt abh ngt. Dies wird als hydrostatischer Druck bezeichnet und ist ein grundlegendes Konzept in der Str mungsmechanik, das verwendet wird, um das Verhalten von Fl ssigkeiten in verschiedenen Anwendungen, wie zum Beispiel in hydraulischen Systemen und Pipelines, zu verstehen.
Die Pascal-Paradoxon bezieht sich auf ein Experiment, das von Blaise Pascal, einem franz sischen Mathematiker und Physiker im 17. Jahrhundert, durchgef hrt wurde. In dem Experiment wurde ein hoher Glaszylinder mit Wasser gef llt und ein langer, schmaler Schlauch wurde durch ein Loch in der Oberseite eingef hrt, wodurch das Wasser im Schlauch eingeschlossen wurde. Obwohl der Schlauch d nn und eine geringe Wassermenge hatte, wurde beobachtet, dass der Druck am unteren Ende des Schlauchs dem Druck am unteren Ende des gr eren Beh lters entsprach.
Ein Beispiel daf r findet sich in dem sogenannten Pascal-Paradoxon, bei dem ein Glasbeh lter mit 50 Litern Wasser durch das Einsetzen eines sehr d nnen Rohres von nur 47 Metern, das nur einen Liter Wasser enth lt, zerspringt. Eine Demonstration dieses Experiments finden Sie in dem folgenden Video:
Der Säulenvolumen ($V$) wird durch die Column Abschnitt ($S$) und die Höhe der Säule ($h$) bestimmt und wird wie folgt berechnet:
Die die Flüssigkeitsdichte ($\rho_w$) wird aus die Masse der Flüssigkeitssäule ($M$) und der Säulenvolumen ($V$) mithilfe der Gleichung berechnet:
Mit die Flüssigkeitsdichte ($\rho_w$), die Column Abschnitt ($S$) und die Höhe der Säule ($h$) kann man die Masse der Flüssigkeitssäule ($M$) mithilfe der Formel berechnen:
Die Schwerkraft ($F_g$) basiert auf die Gravitationsmasse ($m_g$) des Objekts und auf einer Konstanten, die die Intensit t der Gravitation an der Oberfl che des Planeten widerspiegelt. Letztere wird durch die Gravitationsbeschleunigung ($g$) identifiziert, was $9.8 m/s^2$ entspricht.
Daraus folgt, dass:
Die Kraft der Säule ($F$) wird aus die Column Abschnitt ($S$), die Flüssigkeitsdichte ($\rho_w$), die Höhe der Säule ($h$) und die Gravitationsbeschleunigung ($g$) berechnet unter Verwendung von:
Die Druck der Wassersäule ($p$) wird aus die Kraft der Säule ($F$) und die Column Abschnitt ($S$) wie folgt berechnet:
Wenn wir den Ausdruck von die Kraft der Säule ($F$) betrachten und durch die Column Abschnitt ($S$) teilen, erhalten wir die Druck der Wassersäule ($p$). Im Laufe dieses Prozesses vereinfachen wir die Column Abschnitt ($S$), sodass es nicht mehr von diesem abh ngig ist. Die resultierende Expression lautet:
Die Druck der Wassersäule ($p$) ist mit die Flüssigkeitsdichte ($\rho_w$), die Höhe der Säule ($h$), die Gravitationsbeschleunigung ($g$) und die Atmosphärischer Druck ($p_0$) gleich:
ID:(874, 0)