Usuario:


Bernoulli con presión hidrostatica
Storyboard

Si consideramos un fluido sin viscosidad y sin turbulencias (flujo laminar), podemos suponer que la energía se conserva y fluye con el líquido (o gas). En estos casos, obtenemos una ecuación que establece que la suma de la densidad de energía cinética y la densidad de energía potencial son constantes.Esto permite calcular cómo evoluciona la velocidad en función de la posición siempre que se conozca la presión existente o cualquier campo de fuerza.El único problema es que la mayoría de los medios presentan una viscosidad relevante y, por lo tanto, tienden a no tener turbulencias o estas son despreciables y el flujo es intrínsecamente turbulento. Por lo tanto, la aplicación de la ley de Bernoulli en este sentido está restringida, o más bien, es una primera aproximación.

>Modelo

ID:(684, 0)


Mecanismos
Concepto


ID:(15486, 0)


Movimiento de un elemento del liquido/gas con el flujo
Concepto

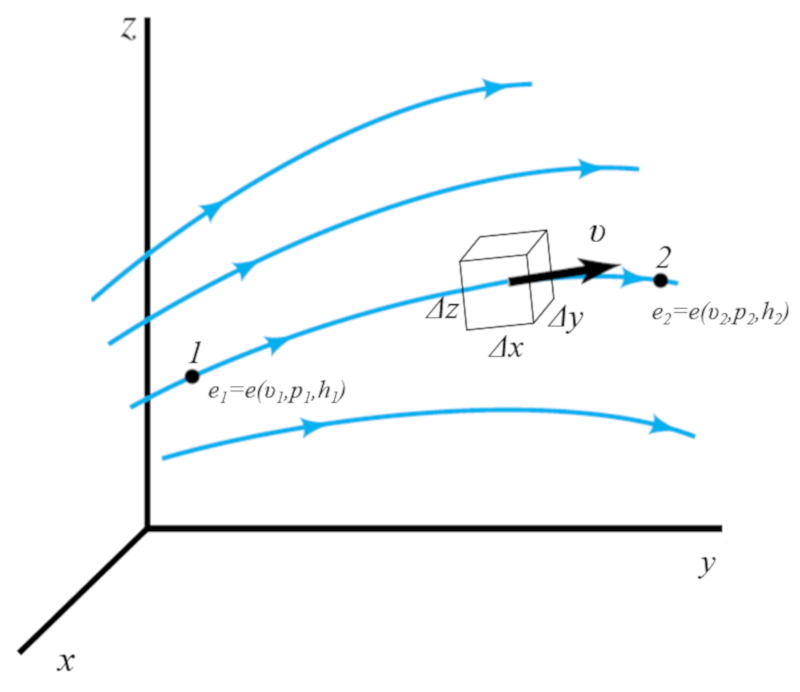
Si consideramos el flujo como una serie de volúmenes con lados $\Delta x$, $\Delta y$ y $\Delta z$ desplazándose en la corriente, podemos asumir que la energía contenida se mantiene constante. Esto implica que la densidad de energía calculada en cualquier punto siempre será la misma.

ID:(11097, 0)


Energía cinetica del elemento en el flujo
Concepto

Si el medio tiene una densidad $\rho$, la masa del volumen $\Delta x\Delta y\Delta z$ se puede calcular como:

$m=\rho\Delta x\Delta y\Delta z$



A partir de esto, podemos estimar la energía cinética del elemento utilizando la velocidad $v$:

$\displaystyle\frac{1}{2}m v^2=\displaystyle\frac{1}{2}\rho\Delta x\Delta y\Delta z v^2$



Esto se puede visualizar en la siguiente imagen:



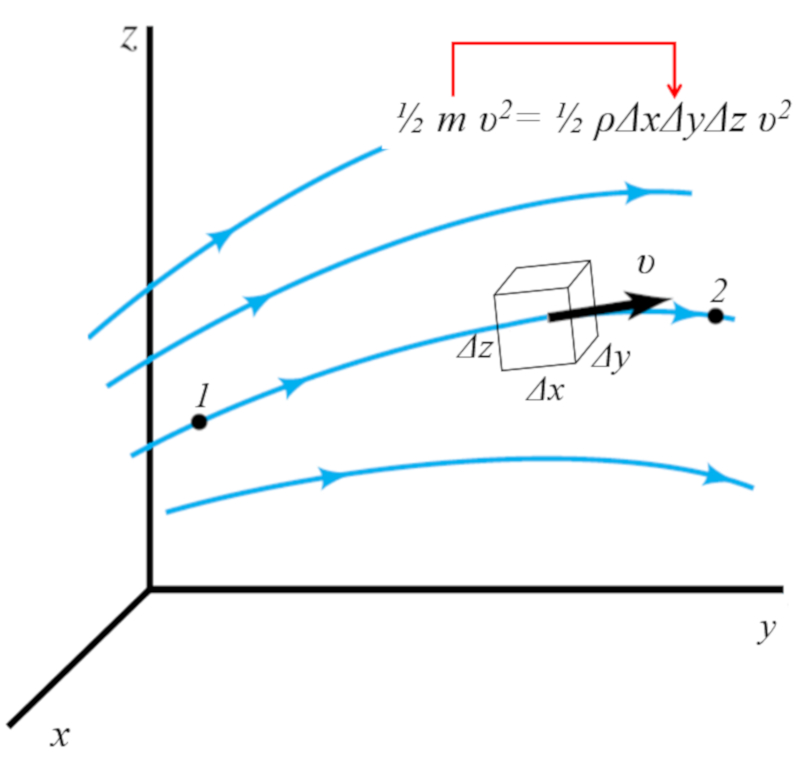
Por ello la densidad de la energía cinetica resulta

$\displaystyle\frac{m v^2}{2 \Delta x\Delta y\Delta z}=\displaystyle\frac{1}{2}\rho v^2$

ID:(11101, 0)


Energía potencial gravitacional del elemento en el flujo
Concepto

Si el medio tiene una densidad de $\rho$ la masa del volumen $\Delta x\Delta y\Delta z$ se puede calcular de

$m=\rho\Delta x\Delta y\Delta z$



con lo que se puede estimar con la altura $h$ la energía potencial gravitacional del elemento

$mgh=\rho\Delta x\Delta y\Delta z gh$



lo que se visualiza en



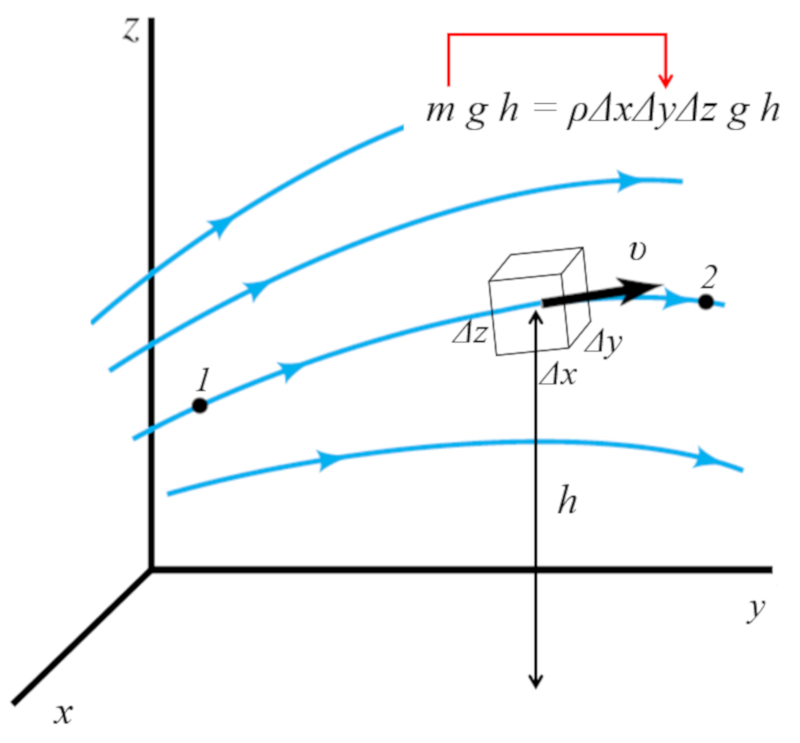
Por ello la densidad de la energía potencial gravitacional resulta

$\displaystyle\frac{mgh}{\Delta x\Delta y\Delta z}=\rho g h$

ID:(11102, 0)


Energía potencial general del elemento en el flujo
Concepto

Si asumimos que existe una fuerza que actúa sobre el elemento y si orientamos el sistema de coordenadas de modo que esta actúe en la dirección x, entonces la fuerza estará realizando un trabajo dado por:

$F\Delta x$



Si la fuerza es generada por una presión, entonces esta actuará sobre la superficie perpendicular a la dirección de la fuerza, es decir, $\Delta y \Delta z$. Por lo tanto, la energía sería:

$F \Delta x= p \Delta S\Delta x = p \Delta x\Delta y\Delta z$



Esto se puede visualizar en la siguiente imagen:



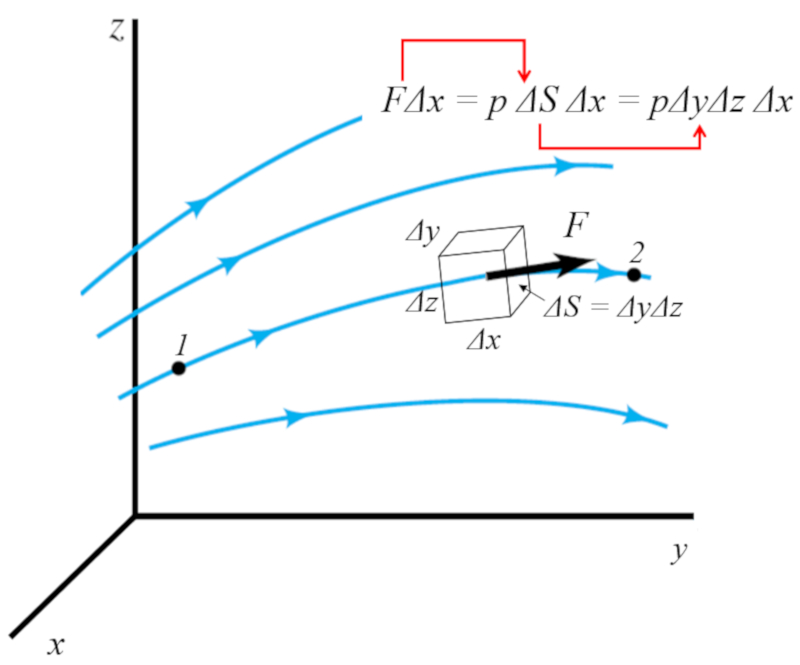
Por ello la densidad de la energía general resulta

$\displaystyle\frac{F \Delta x}{\Delta x\Delta y\Delta z}=\displaystyle\frac{p \Delta x\Delta y\Delta z}{\Delta x\Delta y\Delta z}=p$

ID:(11103, 0)


Densidad de energía
Concepto

La hipótesis de Bernoulli postula que la energía se conserva localmente, es decir, no hay mecanismos que permitan que un volumen del medio intercambie energía con su entorno. Si consideramos la ecuación de energía $E$, que incluye:

• La energía cinética en función de la masa $m$ y la velocidad en un radio del cilindro ($v$),
• La energía potencial gravitacional en función de la aceleración gravitacional ($g$) y la altura de la columna ($h$), y
• Una fuerza externa $F$ que desplaza el líquido una distancia $\Delta z$,
podemos expresarla de esta manera:

$E=\displaystyle\frac{m}{2}v^2+mgh+F\Delta x$



Si consideramos la energía en un volumen $\Delta x\Delta y\Delta z$, podemos reemplazar la masa por la densidad ($\rho$):

$m=\rho \Delta x\Delta y\Delta z$



Y como la presión de la columna de agua ($p$) se expresa como:

$F=p \Delta S =p \Delta y\Delta z$



Obtenemos la ecuación de la densidad de energía ($e$):

$ e =\displaystyle\frac{1}{2} \rho v ^2+ \rho g h + p $



En ausencia de viscosidad, la conservación de energía implica que la densidad de energía ($e$) es constante en cualquier punto del fluido. Por lo tanto, conocer la velocidad y/o la presión en cualquier lugar del fluido es suficiente para establecer una relación entre la velocidad y la presión en cualquier punto del fluido.

ID:(15708, 0)


Ley de Bernoulli y sus límites
Concepto

La hipótesis de la ley de Bernoulli es que la energía, y por ende la densidad de energía ($e$), es constante. En este caso, la densidad de energía es la suma de:

• Cinética, que depende de la densidad del líquido ($\rho_w$) y la velocidad en un radio del cilindro ($v$)
• Potencial gravitacional, que depende de la aceleración gravitacional ($g$) y la altura de la columna ($h$)
• Potencial en general, que depende de la presión ($p$)
lo que resulta en:

$ e =\displaystyle\frac{1}{2} \rho v ^2+ \rho g h + p $

Sin embargo, esto limita la aplicabilidad de la ley debido a que:• La viscosidad es un proceso en el que la energía se difunde a través del medio y, en este sentido, la energía no se conserva localmente ya que se redistribuye en el medio.• No pueden existir vórtices, ya que estos presentan inherentemente zonas de densidades de energía diferentes y, por lo tanto, contravienen la hipótesis. Esto significa que la ley no describiría un flujo turbulento.El problema es que en la mayoría de los casos, el flujo puede ser dominado por la viscosidad, denominándose el flujo como "laminar", o dominado por la inercia, lo que observamos como un flujo "turbulento". Por lo tanto, la ley de Bernoulli es un modelo solo aplicable en situaciones en las que la inhomogeneidad de la densidad de energía es menor.

ID:(15500, 0)


Ecuación de Bernoulli general
Concepto

Si asumimos que la densidad de energía ($e$) se conserva, podemos afirmar que para una celda en la que la velocidad media es la velocidad en un radio del cilindro ($v$), la densidad es la densidad ($\rho$), la presión es la presión de la columna de agua ($p$), la altura es la altura de la columna ($h$) y la aceleración gravitacional es la aceleración gravitacional ($g$), se cumple lo siguiente:

$ e =\displaystyle\frac{1}{2} \rho v ^2+ \rho g h + p $



En un punto 1, esta ecuación será igual a la misma ecuación en un punto 2:

$e(v_1,p_1,h_1)=e(v_2,p_2,h_2)$



con la velocidad media del fluido en el punto 1 ($v_1$), la altura o profundidad 1 ($h_1$) y la presión en la columna 1 ($p_1$) representan la velocidad, altura y presión en el punto 1, respectivamente, y la velocidad media del fluido en el punto 2 ($v_2$), la altura o profundidad 2 ($h_2$) y la presión en la columna 2 ($p_2$) representan la velocidad, altura y presión en el punto 2, respectivamente.

Por lo tanto, se tiene la ecuación de Bernoulli [1]:

$\displaystyle\frac{1}{2} \rho v_1 ^2+ \rho g h_1 + p_1 =\displaystyle\frac{1}{2} \rho v_2 ^2+ \rho g h_2 + p_2 $



[1] "Hydrodynamica" (Hidrodinamica), Daniel Bernoulli, Typis Joh. Henr. Deckeri (1738)

Es importante tener en cuenta que se han hecho las siguientes suposiciones:

Se conserva la energía, en particular, se supone la ausencia de viscosidad.


No hay deformación en el medio, por lo tanto, la densidad no varía.


No hay vorticidad, es decir, no hay torbellinos que generen circulación en el medio. El fluido debe presentar un comportamiento laminar.

ID:(15707, 0)


Dispensador de perfume
Descripción

En los dispensadores de perfume, se crea un flujo de aire sobre un tubo sumergido en el perfume. Esto genera una disminución de la presión, lo que provoca que la presión en la columna de perfume sea menor que la columna generada por el líquido dentro del frasco. Como resultado, el líquido es impulsado a través de la columna. Finalmente, el líquido que alcanza la parte superior es pulverizado y transportado por el chorro de aire.



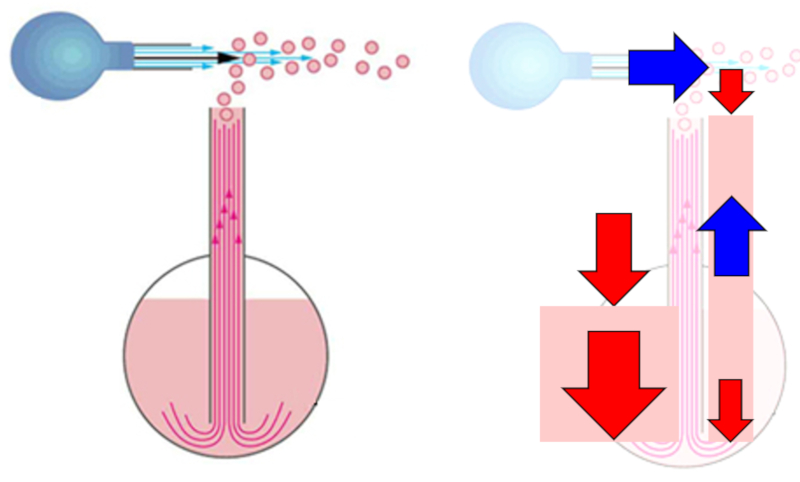
Para modelar el sistema, se puede utilizar la ley de Bernoulli con la densidad del líquido la densidad del líquido ($\rho_w$) y la altura la aceleración gravitacional ($g$). Si el punto 1 está en la base del tubo de transporte del líquido, entonces la velocidad media del fluido en el punto 1 ($v_1$) es nulo, la altura o profundidad 1 ($h_1$) es la profundidad del líquido ($h$), y la presión en la columna 1 ($p_1$) es la presión atmosférica. Si el punto 2 está en la salida superior del tubo de transporte del líquido, entonces la velocidad media del fluido en el punto 2 ($v_2$) es la velocidad con la que emerge el líquido ($v$), la altura o profundidad 2 ($h_2$) es nulo, y la presión en la columna 2 ($p_2$) es la presión atmosférica. Por lo tanto, la expresión

$\displaystyle\frac{1}{2} \rho v_1 ^2+ \rho g h_1 + p_1 =\displaystyle\frac{1}{2} \rho v_2 ^2+ \rho g h_2 + p_2 $



se reduce a

$\rho g h=\displaystyle\frac{1}{2}\rho v^2 $



ya que la presión atmosférica se simplifica. Con ello, la velocidad con la que emerge el líquido es:

$v = \sqrt{ 2 g h }$

ID:(11096, 0)


Modelo
Concepto


ID:(15489, 0)


Bernoulli con presión hidrostatica
Descripción

Si consideramos un fluido sin viscosidad y sin turbulencias (flujo laminar), podemos suponer que la energía se conserva y fluye con el líquido (o gas). En estos casos, obtenemos una ecuación que establece que la suma de la densidad de energía cinética y la densidad de energía potencial son constantes. Esto permite calcular cómo evoluciona la velocidad en función de la posición siempre que se conozca la presión existente o cualquier campo de fuerza. El único problema es que la mayoría de los medios presentan una viscosidad relevante y, por lo tanto, tienden a no tener turbulencias o estas son despreciables y el flujo es intrínsecamente turbulento. Por lo tanto, la aplicación de la ley de Bernoulli en este sentido está restringida, o más bien, es una primera aproximación.

Variables
Símbolo
Texto
Variable
Valor
Unidades
Calcule
Valor MKS
Unidades MKS
$\Delta h$
Dh
Altura de la columna del liquido
m
$h_1$
h_1
Altura o profundidad 1
m
$h_2$
h_2
Altura o profundidad 2
m
$\rho$
rho
Densidad
kg/m^3
$e_1$
e_1
Densidad de energía en 1
J/m^3
$e_2$
e_2
Densidad de energía en 2
J/m^3
$\Delta v$
Dv
Diferencia de velocidad entre superficies
m/s
$\Delta p$
Dp
Diferencial de la presión
Pa
$p_1$
p_1
Presión en la columna 1
Pa
$p_2$
p_2
Presión en la columna 2
Pa
$v_1$
v_1
Velocidad media del fluido en el punto 1
m/s
$v_2$
v_2
Velocidad media del fluido en el punto 2
m/s

Cálculos

Primero, seleccione la ecuación:   a ,  luego, seleccione la variable:   a 
Símbolo
Ecuación
Resuelto
Traducido

Cálculos

Símbolo
Ecuación
Resuelto
Traducido

 Variable   Dado   Calcule   Objetivo :   Ecuación   A utilizar


Ecuaciones

Otra ecuaci n til es la que corresponde a la conservaci n de energ a, que se aplica en casos donde la viscosidad, un proceso en el cual se pierde energ a, puede ser despreciada. Si consideramos la cl sica ecuaci n de energ a $E$, que incluye la energ a cin tica, la energ a potencial gravitacional y una fuerza externa que desplaza el l quido una distancia $\Delta z$, podemos expresarla de la siguiente manera:

$E=\displaystyle\frac{m}{2}v^2+mgh+F\Delta x$



Si consideramos la energ a en un volumen $\Delta x\Delta y\Delta z$, podemos reemplazar la masa por:

$m=\rho \Delta x\Delta y\Delta z$



Y como la presi n se expresa como:

$F=p \Delta S =p \Delta y\Delta z$



Obtenemos la ecuaci n de densidad de energ a:

$ e =\displaystyle\frac{1}{2} \rho v ^2+ \rho g h + p $

(ID 3159)

Otra ecuaci n til es la que corresponde a la conservaci n de energ a, que se aplica en casos donde la viscosidad, un proceso en el cual se pierde energ a, puede ser despreciada. Si consideramos la cl sica ecuaci n de energ a $E$, que incluye la energ a cin tica, la energ a potencial gravitacional y una fuerza externa que desplaza el l quido una distancia $\Delta z$, podemos expresarla de la siguiente manera:

$E=\displaystyle\frac{m}{2}v^2+mgh+F\Delta x$



Si consideramos la energ a en un volumen $\Delta x\Delta y\Delta z$, podemos reemplazar la masa por:

$m=\rho \Delta x\Delta y\Delta z$



Y como la presi n se expresa como:

$F=p \Delta S =p \Delta y\Delta z$



Obtenemos la ecuaci n de densidad de energ a:

$ e =\displaystyle\frac{1}{2} \rho v ^2+ \rho g h + p $

(ID 3159)

Si hay la diferencia de presión ($\Delta p$) entre dos puntos, como lo indica la ecuaci n:

$ dp = p - p_0 $



podemos usar la presión de la columna de agua ($p$), que es:

$ p_t = p_0 + \rho_w g h $



Esto nos da:

$\Delta p=p_2-p_1=p_0+\rho_wh_2g-p_0-\rho_wh_1g=\rho_w(h_2-h_1)g$



Dado que la diferencia de altura ($\Delta h$) es:

$ \Delta h = h_2 - h_1 $



la diferencia de presión ($\Delta p$) se puede expresar como:

$ \Delta p = \rho_w g \Delta h $

(ID 4345)

Si asumimos que la densidad de energía ($e$) se conserva, podemos afirmar que para una celda en la que la velocidad media es la velocidad en un radio del cilindro ($v$), la densidad es la densidad ($\rho$), la presi n es la presión de la columna de agua ($p$), la altura es la altura de la columna ($h$) y la aceleraci n gravitacional es la aceleración gravitacional ($g$), se cumple lo siguiente:

$ e =\displaystyle\frac{1}{2} \rho v ^2+ \rho g h + p $



En un punto 1, esta ecuaci n ser igual a la misma ecuaci n en un punto 2:

$e(v_1,p_1,h_1)=e(v_2,p_2,h_2)$



con la velocidad media del fluido en el punto 1 ($v_1$), la altura o profundidad 1 ($h_1$) y la presión en la columna 1 ($p_1$) representan la velocidad, altura y presi n en el punto 1, respectivamente, y la velocidad media del fluido en el punto 2 ($v_2$), la altura o profundidad 2 ($h_2$) y la presión en la columna 2 ($p_2$) representan la velocidad, altura y presi n en el punto 2, respectivamente. Por lo tanto, se tiene:

$\displaystyle\frac{1}{2} \rho v_1 ^2+ \rho g h_1 + p_1 =\displaystyle\frac{1}{2} \rho v_2 ^2+ \rho g h_2 + p_2 $

(ID 4504)

Ejemplos


(ID 15486)

Si consideramos el flujo como una serie de vol menes con lados $\Delta x$, $\Delta y$ y $\Delta z$ desplaz ndose en la corriente, podemos asumir que la energ a contenida se mantiene constante. Esto implica que la densidad de energ a calculada en cualquier punto siempre ser la misma.

(ID 11097)

Si el medio tiene una densidad $\rho$, la masa del volumen $\Delta x\Delta y\Delta z$ se puede calcular como:

$m=\rho\Delta x\Delta y\Delta z$



A partir de esto, podemos estimar la energ a cin tica del elemento utilizando la velocidad $v$:

$\displaystyle\frac{1}{2}m v^2=\displaystyle\frac{1}{2}\rho\Delta x\Delta y\Delta z v^2$



Esto se puede visualizar en la siguiente imagen:



Por ello la densidad de la energ a cinetica resulta

$\displaystyle\frac{m v^2}{2 \Delta x\Delta y\Delta z}=\displaystyle\frac{1}{2}\rho v^2$

(ID 11101)

Si el medio tiene una densidad de $\rho$ la masa del volumen $\Delta x\Delta y\Delta z$ se puede calcular de

$m=\rho\Delta x\Delta y\Delta z$



con lo que se puede estimar con la altura $h$ la energ a potencial gravitacional del elemento

$mgh=\rho\Delta x\Delta y\Delta z gh$



lo que se visualiza en



Por ello la densidad de la energ a potencial gravitacional resulta

$\displaystyle\frac{mgh}{\Delta x\Delta y\Delta z}=\rho g h$

(ID 11102)

Si asumimos que existe una fuerza que act a sobre el elemento y si orientamos el sistema de coordenadas de modo que esta act e en la direcci n x, entonces la fuerza estar realizando un trabajo dado por:

$F\Delta x$



Si la fuerza es generada por una presi n, entonces esta actuar sobre la superficie perpendicular a la direcci n de la fuerza, es decir, $\Delta y \Delta z$. Por lo tanto, la energ a ser a:

$F \Delta x= p \Delta S\Delta x = p \Delta x\Delta y\Delta z$



Esto se puede visualizar en la siguiente imagen:



Por ello la densidad de la energ a general resulta

$\displaystyle\frac{F \Delta x}{\Delta x\Delta y\Delta z}=\displaystyle\frac{p \Delta x\Delta y\Delta z}{\Delta x\Delta y\Delta z}=p$

(ID 11103)

La hip tesis de Bernoulli postula que la energ a se conserva localmente, es decir, no hay mecanismos que permitan que un volumen del medio intercambie energ a con su entorno. Si consideramos la ecuaci n de energ a $E$, que incluye:

• La energ a cin tica en funci n de la masa $m$ y la velocidad en un radio del cilindro ($v$),
• La energ a potencial gravitacional en funci n de la aceleración gravitacional ($g$) y la altura de la columna ($h$), y
• Una fuerza externa $F$ que desplaza el l quido una distancia $\Delta z$,
podemos expresarla de esta manera:

$E=\displaystyle\frac{m}{2}v^2+mgh+F\Delta x$



Si consideramos la energ a en un volumen $\Delta x\Delta y\Delta z$, podemos reemplazar la masa por la densidad ($\rho$):

$m=\rho \Delta x\Delta y\Delta z$



Y como la presión de la columna de agua ($p$) se expresa como:

$F=p \Delta S =p \Delta y\Delta z$



Obtenemos la ecuaci n de la densidad de energía ($e$):

$ e =\displaystyle\frac{1}{2} \rho v ^2+ \rho g h + p $



En ausencia de viscosidad, la conservaci n de energ a implica que la densidad de energía ($e$) es constante en cualquier punto del fluido. Por lo tanto, conocer la velocidad y/o la presi n en cualquier lugar del fluido es suficiente para establecer una relaci n entre la velocidad y la presi n en cualquier punto del fluido.

(ID 15708)

La hip tesis de la ley de Bernoulli es que la energ a, y por ende la densidad de energía ($e$), es constante. En este caso, la densidad de energ a es la suma de:

• Cin tica, que depende de la densidad del líquido ($\rho_w$) y la velocidad en un radio del cilindro ($v$)
• Potencial gravitacional, que depende de la aceleración gravitacional ($g$) y la altura de la columna ($h$)
• Potencial en general, que depende de la presión ($p$)
lo que resulta en:

$ e =\displaystyle\frac{1}{2} \rho v ^2+ \rho g h + p $

Sin embargo, esto limita la aplicabilidad de la ley debido a que:• La viscosidad es un proceso en el que la energ a se difunde a trav s del medio y, en este sentido, la energ a no se conserva localmente ya que se redistribuye en el medio.• No pueden existir v rtices, ya que estos presentan inherentemente zonas de densidades de energ a diferentes y, por lo tanto, contravienen la hip tesis. Esto significa que la ley no describir a un flujo turbulento.El problema es que en la mayor a de los casos, el flujo puede ser dominado por la viscosidad, denomin ndose el flujo como "laminar", o dominado por la inercia, lo que observamos como un flujo "turbulento". Por lo tanto, la ley de Bernoulli es un modelo solo aplicable en situaciones en las que la inhomogeneidad de la densidad de energ a es menor.

(ID 15500)

Si asumimos que la densidad de energía ($e$) se conserva, podemos afirmar que para una celda en la que la velocidad media es la velocidad en un radio del cilindro ($v$), la densidad es la densidad ($\rho$), la presi n es la presión de la columna de agua ($p$), la altura es la altura de la columna ($h$) y la aceleraci n gravitacional es la aceleración gravitacional ($g$), se cumple lo siguiente:

$ e =\displaystyle\frac{1}{2} \rho v ^2+ \rho g h + p $



En un punto 1, esta ecuaci n ser igual a la misma ecuaci n en un punto 2:

$e(v_1,p_1,h_1)=e(v_2,p_2,h_2)$



con la velocidad media del fluido en el punto 1 ($v_1$), la altura o profundidad 1 ($h_1$) y la presión en la columna 1 ($p_1$) representan la velocidad, altura y presi n en el punto 1, respectivamente, y la velocidad media del fluido en el punto 2 ($v_2$), la altura o profundidad 2 ($h_2$) y la presión en la columna 2 ($p_2$) representan la velocidad, altura y presi n en el punto 2, respectivamente.

Por lo tanto, se tiene la ecuaci n de Bernoulli [1]:

$\displaystyle\frac{1}{2} \rho v_1 ^2+ \rho g h_1 + p_1 =\displaystyle\frac{1}{2} \rho v_2 ^2+ \rho g h_2 + p_2 $



[1] "Hydrodynamica" (Hidrodinamica), Daniel Bernoulli, Typis Joh. Henr. Deckeri (1738)

Es importante tener en cuenta que se han hecho las siguientes suposiciones:

Se conserva la energ a, en particular, se supone la ausencia de viscosidad.


No hay deformaci n en el medio, por lo tanto, la densidad no var a.


No hay vorticidad, es decir, no hay torbellinos que generen circulaci n en el medio. El fluido debe presentar un comportamiento laminar.

(ID 15707)

En los dispensadores de perfume, se crea un flujo de aire sobre un tubo sumergido en el perfume. Esto genera una disminuci n de la presi n, lo que provoca que la presi n en la columna de perfume sea menor que la columna generada por el l quido dentro del frasco. Como resultado, el l quido es impulsado a trav s de la columna. Finalmente, el l quido que alcanza la parte superior es pulverizado y transportado por el chorro de aire.



Para modelar el sistema, se puede utilizar la ley de Bernoulli con la densidad del l quido la densidad del líquido ($\rho_w$) y la altura la aceleración gravitacional ($g$). Si el punto 1 est en la base del tubo de transporte del l quido, entonces la velocidad media del fluido en el punto 1 ($v_1$) es nulo, la altura o profundidad 1 ($h_1$) es la profundidad del l quido ($h$), y la presión en la columna 1 ($p_1$) es la presi n atmosf rica. Si el punto 2 est en la salida superior del tubo de transporte del l quido, entonces la velocidad media del fluido en el punto 2 ($v_2$) es la velocidad con la que emerge el l quido ($v$), la altura o profundidad 2 ($h_2$) es nulo, y la presión en la columna 2 ($p_2$) es la presi n atmosf rica. Por lo tanto, la expresi n

$\displaystyle\frac{1}{2} \rho v_1 ^2+ \rho g h_1 + p_1 =\displaystyle\frac{1}{2} \rho v_2 ^2+ \rho g h_2 + p_2 $



se reduce a

$\rho g h=\displaystyle\frac{1}{2}\rho v^2 $



ya que la presi n atmosf rica se simplifica. Con ello, la velocidad con la que emerge el l quido es:

$v = \sqrt{ 2 g h }$

(ID 11096)


(ID 15489)

ID:(684, 0)