En columna de liquido
Storyboard 
En el caso de una columna de líquido, se puede aplicar la ley de Bernoulli junto con el término de presión hidrostática. Sin embargo, es importante tener en cuenta que al no considerar la viscosidad del líquido, la reducción del nivel ocurre de manera uniforme. En este sentido, se puede modelar utilizando la ley de continuidad para determinar la velocidad de descenso del cilindro.
Para una columna de líquido con salida en el fondo, se observa que el comportamiento es similar a lo que se estima con Bernoulli. Las diferencias surgen debido a la formación de pequeños torbellinos en la salida, que efectivamente reducen la sección de salida y obstruyen el flujo. Sin embargo, el flujo de un líquido con baja viscosidad se puede modelar en la zona que no presenta torbellinos con la ley de Bernoulli.
ID:(1427, 0)
Presión estatica y dinamica
Imagen 
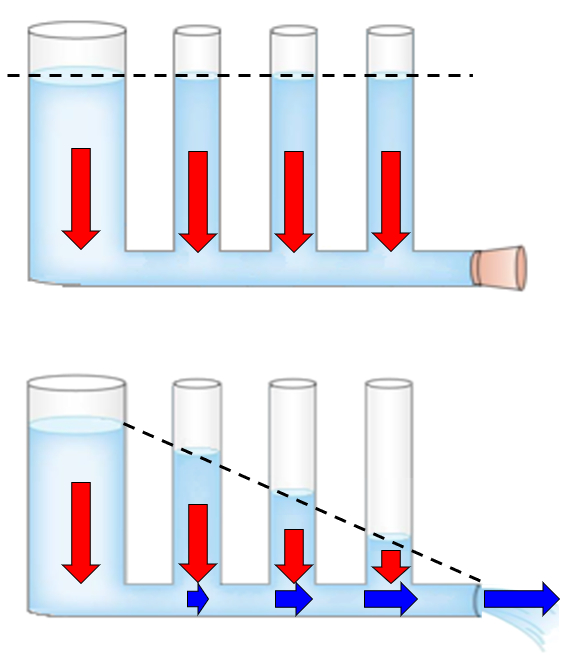
Cuando se tienen cuatro columnas de diferentes secciones intercomunicadas, el líquido adoptará el mismo nivel en todas ellas. Si se abre el conducto de comunicación, el líquido comenzará a fluir en dirección a la abertura donde la presión es igual a la presión ambiente. En el primer cilindro, la presión es igual a la de la columna de agua y la presión atmosférica, por lo que la diferencia con respecto a la presión en la salida es la presión de la primera columna. El líquido comienza a adquirir velocidad mientras que la presión dinámica comienza a disminuir, lo que se aprecia en columnas cada vez más pequeñas.
ID:(11092, 0)
Experimento de vaciado de columna
Nota 
Esto significa que a medida que la columna se va vaciando y la altura $h$ se reduce, la velocidad $v$ también disminuye de manera proporcional.
Los parámetros clave son:
• Diámetro interior de la cubeta: 93 mm
• Diámetro interior del canal de evacuación: 3 mm
• Longitud del canal de evacuación: 18 mm
Estos parámetros son importantes para comprender y analizar el proceso de vaciado de la columna y cómo la velocidad de salida varía con la altura.
ID:(9870, 0)
En columna de liquido
Descripción 
En el caso de una columna de líquido, se puede aplicar la ley de Bernoulli junto con el término de presión hidrostática. Sin embargo, es importante tener en cuenta que al no considerar la viscosidad del líquido, la reducción del nivel ocurre de manera uniforme. En este sentido, se puede modelar utilizando la ley de continuidad para determinar la velocidad de descenso del cilindro. Para una columna de líquido con salida en el fondo, se observa que el comportamiento es similar a lo que se estima con Bernoulli. Las diferencias surgen debido a la formación de pequeños torbellinos en la salida, que efectivamente reducen la sección de salida y obstruyen el flujo. Sin embargo, el flujo de un líquido con baja viscosidad se puede modelar en la zona que no presenta torbellinos con la ley de Bernoulli.
Variables
Cálculos
Cálculos
Ecuaciones
(ID 3469)
(ID 3804)
Si hay la diferencia de presión ($\Delta p$) entre dos puntos, como lo indica la ecuaci n:
| $ dp = p - p_0 $ |
podemos usar la presión de la columna de agua ($p$), que es:
| $ p_t = p_0 + \rho_w g h $ |
Esto nos da:
$\Delta p=p_2-p_1=p_0+\rho_wh_2g-p_0-\rho_wh_1g=\rho_w(h_2-h_1)g$
Dado que la diferencia de altura ($\Delta h$) es:
| $ \Delta h = h_2 - h_1 $ |
la diferencia de presión ($\Delta p$) se puede expresar como:
| $ \Delta p = \rho_w g \Delta h $ |
(ID 4345)
La continuidad implica que el flujo de volumen 1 ($J_{V1}$) y el flujo de volumen 2 ($J_{V2}$) son iguales
| $ J_{V1} = J_{V2} $ |
lleva a que la densidad de flujo 1 ($j_{s1}$) por la sección en el punto 1 ($S_1$)
| $ j_s = \displaystyle\frac{ J_V }{ S }$ |
y a que la densidad de flujo 2 ($j_{s2}$) por la velocidad máxima en el flujo por un cilindro ($v_{max}$)
| $ j_s = \displaystyle\frac{ J_V }{ S }$ |
se obtiene que
| $ S_1 j_{s1} = S_2 j_{s2} $ |
(ID 4350)
A partir de la ecuaci n de Bernoulli, podemos analizar el caso de una columna de agua que genera una diferencia de presi n:
| $ \Delta p = \rho_w g \Delta h $ |
y provoca un flujo de velocidad $v$ a trav s de un tubo, de acuerdo con:
| $ \Delta p = - \rho \bar{v} \Delta v $ |
Por lo tanto, podemos estimar la velocidad como:
$v = \sqrt{2 g h}$
Esta velocidad, a trav s de una secci n de tubo de radio $R$, genera un flujo:
$J = \pi R^2 v$
Si la columna tiene una secci n $S$ y su altura disminuye con respecto a la variaci n de la altura $h$ en el tiempo $t$, podemos aplicar la ley de continuidad, que establece:
| $ S_1 j_{s1} = S_2 j_{s2} $ |
Entonces, la ecuaci n que describe esta situaci n es:
| $ S\displaystyle\frac{dh}{dt} = \pi R^2 \sqrt{2gh}$ |
(ID 9882)
Si en la ecuaci n
| $ S\displaystyle\frac{dh}{dt} = \pi R^2 \sqrt{2gh}$ |
se reemplazan las constantes mediante
| $ \tau_b = \displaystyle\frac{S}{\pi R^2}\sqrt{\displaystyle\frac{h_0}{g}}$ |
obtenemos la ecuaci n diferencial lineal de primer orden
$\displaystyle\frac{dh}{dt}=\displaystyle\frac{1}{\tau_b} \sqrt{h_0 h}$
cuya soluci n es
| $ h = h_0\left(1-\displaystyle\frac{t}{\tau_b}\right)^2$ |
(ID 14524)
En este caso, se puede asumir que la velocidad media del fluido en el punto 2 ($v_2$) representa una velocidad nula y la velocidad media del fluido en el punto 1 ($v_1$) equivale a la velocidad del flujo ($v_s$), por lo que
| $ \Delta v = v_2 - v_1 $ |
para la diferencia de velocidad entre superficies ($\Delta v$) se obtiene:
$\Delta v = v_2 - v_1 = 0 - v_s = - v_s$
y para la velocidad promedio ($\bar{v}$)
| $ \bar{v} = \displaystyle\frac{ v_1 + v_2 }{2}$ |
se calcula:
$\bar{v} = \displaystyle\frac{v_1 + v_2}{2} = \displaystyle\frac{v_s}{2}$
Consecuentemente, con el diferencial de la presión ($\Delta p$), que es equivalente a la diferencia de presión ($\Delta p_s$), se obtiene:
| $ \Delta p = - \rho \bar{v} \Delta v $ |
resultando en:
$\Delta p_s = \displaystyle\frac{1}{2} \rho v_s^2$
lo que conduce a:
| $ v_s = \sqrt{\displaystyle\frac{2 \Delta p_s }{ \rho }}$ |
(ID 15710)
El volumen ($V$) para un tubo con la sección del tubo ($S$) constante y una posición ($s$) es
| $ V = h S $ |
Si la sección del tubo ($S$) es constante, la derivada temporal ser
$\displaystyle\frac{dV}{dt} = S\displaystyle\frac{ds}{dt}$
por lo que, con el flujo de volumen ($J_V$) definido por
| $ J_V =\displaystyle\frac{ dV }{ dt }$ |
y con la densidad de flujo ($j_s$) asociado a la posición ($s$) mediante
| $ j_s =\displaystyle\frac{ ds }{ dt }$ |
se concluye que
| $ J_V = S j_s $ |
(ID 15716)
Ejemplos
(ID 15487)
Si se tiene una altura de la columna ($h$) de l quido con la densidad del líquido ($\rho_w$) bajo el efecto de la gravedad, utilizando la aceleración gravitacional ($g$), se genera el diferencial de la presión ($\Delta p$) de acuerdo con:
| $ \Delta p = \rho_w g \Delta h $ |
Esta el diferencial de la presión ($\Delta p$) produce, a trav s del tubo de salida con el largo de tubo ($\Delta L$), el radio del tubo ($R$) y la viscosidad ($\eta$), un flujo de un flujo de volumen 1 ($J_{V1}$) seg n la ley de Hagen-Poiseuille:
| $ J_V =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
Dado que esta ecuaci n incluye la sección en el punto 2 ($S_2$), es posible calcular la densidad de flujo 2 ($j_{s2}$) mediante:
| $ j_s = \displaystyle\frac{ J_V }{ S }$ |
Con esto, se obtiene:
| $ j_s = \displaystyle\frac{ \rho_w g R ^2}{8 \eta \Delta L } h $ |
que corresponde a una velocidad media.
Para modelar el sistema, los par metros clave son:
• Di metro interior de la cubeta: 93 mm
• Di metro interior del canal de evacuaci n: 3,2 mm
• Longitud del canal de evacuaci n: 18 mm
La altura inicial del l quido es de 25 cm.
(ID 11092)
Consideremos el sistema de un cubo cil ndrico con un agujero de evacuaci n. Al retirar el tap n, el agua comienza a fluir en funci n de la presi n existente. Seg n Bernoulli en el interior ($v\sim 0$), la velocidad es nula y tenemos:
$\displaystyle\frac{1}{2}\rho v^2 + \rho g h\sim \rho g h$
mientras que en el exterior ($h=0$), solo existe la componente cin tica:
$\displaystyle\frac{1}{2}\rho v^2 + \rho g h\sim \displaystyle\frac{1}{2}\rho v^2$
Como ambas expresiones son iguales, tenemos:
$\displaystyle\frac{1}{2}\rho v^2=\rho g h$
por lo que la velocidad es:
$v=\sqrt{2 g h}$
Para comparar con el experimento, podemos utilizar esta expresi n para estimar con:
| $ S\displaystyle\frac{dh}{dt} = \pi R^2 \sqrt{2gh}$ |
el alcance que deber a tener el chorro. Si lo representamos gr ficamente, observamos:
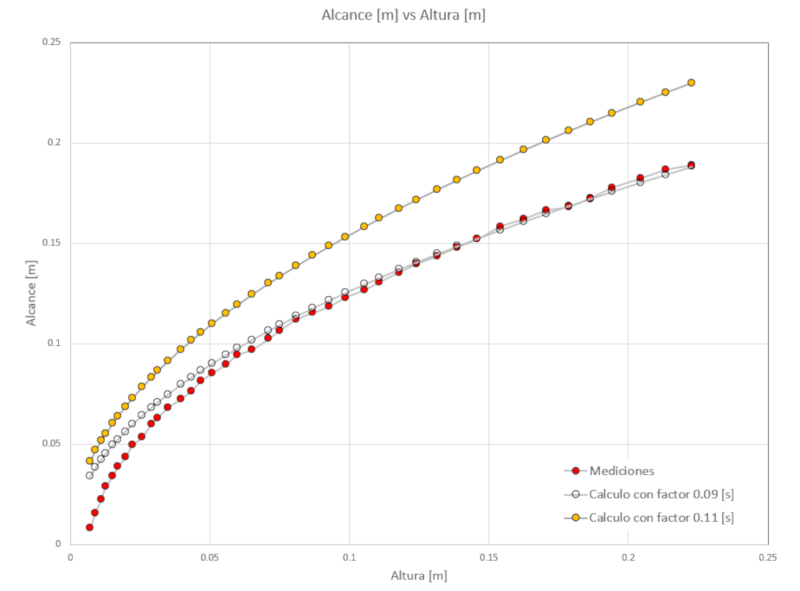
donde:
• los puntos rojos corresponden a las mediciones experimentales,
• los puntos azules corresponden al alcance calculado utilizando un factor de 0.11,
• los puntos transparentes corresponden al alcance calculado utilizando un factor de 0.09.
Por lo tanto, podemos concluir que el modelo de Bernoulli sobreestima la velocidad a la que se vac a el cubo. Esto se debe a que en la zona del agujero de evacuaci n, los efectos de la viscosidad no son despreciables y, por lo tanto, la velocidad es menor.
(ID 11063)
Si se utiliza el programa Tracker, se puede medir la altura del menisco de la columna y el alcance del chorro. La relaci n entre ambos se muestra en el siguiente gr fico:
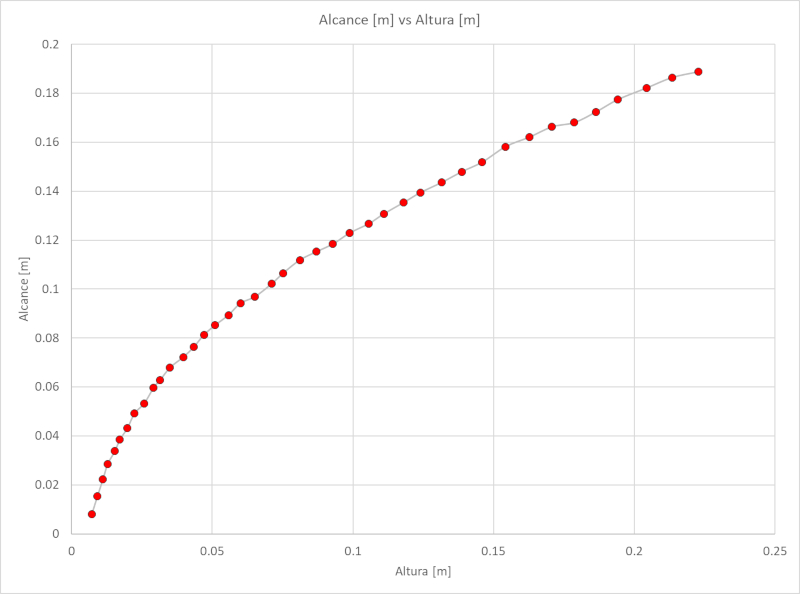
Alcance [m] vs Altura [m]
Los datos registrados, que se pueden descargar como tabla de Excel en el siguiente enlace tabla excel, son los siguientes:
| Tiempo [s] | Altura [m] | Alcance [m] |
| 0 | 2.23E-01 | 1.89E-01 |
| 4 | 2.14E-01 | 1.86E-01 |
| 8 | 2.04E-01 | 1.82E-01 |
| 12 | 1.94E-01 | 1.77E-01 |
| 16 | 1.86E-01 | 1.72E-01 |
| 20 | 1.79E-01 | 1.68E-01 |
| 24 | 1.71E-01 | 1.66E-01 |
| 28 | 1.63E-01 | 1.62E-01 |
| 32 | 1.54E-01 | 1.58E-01 |
| 36 | 1.46E-01 | 1.52E-01 |
| 40 | 1.39E-01 | 1.48E-01 |
| 44 | 1.32E-01 | 1.44E-01 |
| 48 | 1.24E-01 | 1.39E-01 |
| 52 | 1.18E-01 | 1.35E-01 |
| 56 | 1.11E-01 | 1.31E-01 |
| 60 | 1.06E-01 | 1.27E-01 |
| 64 | 9.88E-02 | 1.23E-01 |
| 68 | 9.29E-02 | 1.18E-01 |
| 72 | 8.70E-02 | 1.15E-01 |
| 76 | 8.11E-02 | 1.12E-01 |
| 80 | 7.52E-02 | 1.06E-01 |
| 84 | 7.12E-02 | 1.02E-01 |
| 88 | 6.51E-02 | 9.69E-02 |
| 92 | 6.00E-02 | 9.42E-02 |
| 96 | 5.58E-02 | 8.94E-02 |
| 100 | 5.09E-02 | 8.52E-02 |
| 104 | 4.70E-02 | 8.13E-02 |
| 108 | 4.34E-02 | 7.63E-02 |
| 112 | 3.97E-02 | 7.22E-02 |
| 116 | 3.49E-02 | 6.79E-02 |
| 120 | 3.15E-02 | 6.28E-02 |
| 124 | 2.91E-02 | 5.96E-02 |
| 128 | 2.58E-02 | 5.33E-02 |
| 132 | 2.23E-02 | 4.92E-02 |
| 136 | 1.98E-02 | 4.31E-02 |
| 140 | 1.71E-02 | 3.85E-02 |
| 144 | 1.54E-02 | 3.38E-02 |
| 148 | 1.28E-02 | 2.85E-02 |
| 152 | 1.11E-02 | 2.23E-02 |
| 156 | 9.17E-03 | 1.54E-02 |
| 160 | 7.15E-03 | 7.95E-03 |
Nota: el E indica notaci n cientifica (ej. 1.2E+3 = 1.2x10^3 = 1200, y 1.2E-3 = 1.2x10^-3 = 0.0012)
(ID 11062)
(ID 15490)
Si tenemos un tubo con una la sección del tubo ($S$) que se desplaza una distancia el elemento del tubo ($\Delta s$) a lo largo de su eje, habiendo trasladado el elemento de volumen ($\Delta V$), igual a:
| $ \Delta V = S \Delta s $ |
(ID 3469)
El flujo de volumen ($J_V$) corresponde a el volumen que fluye ($\Delta V$) que fluye a trav s del canal en el tiempo transcurrido ($\Delta t$). Por lo tanto, tenemos:
| $ J_V =\displaystyle\frac{ \Delta V }{ \Delta t }$ |
(ID 4347)
La densidad de flujo ($j_s$) se relaciona con la distancia recorrida en un tiempo ($\Delta s$), que es la distancia que el fluido recorre en el tiempo transcurrido ($\Delta t$), de la siguiente manera:
| $ j_s =\displaystyle\frac{ \Delta s }{ \Delta t }$ |
(ID 4348)
Se puede representar una densidad de flujo ($j_s$) en t rminos de el flujo de volumen ($J_V$) utilizando la sección o superficie ($S$) mediante la siguiente f rmula:
| $ J_V = S j_s $ |
(ID 15716)
La superficie de un disco ($S$) de un radio de un disco ($r$) se calcula de la siguiente manera:
| $ S = \pi r ^2$ |
(ID 3804)
Cuando se aplica la ecuaci n de Bernoulli en relaci n con un punto en reposo dentro del flujo, se establece que la velocidad del flujo ($v_s$) se asocia con la diferencia de presión ($\Delta p_s$) en cuanto a la presi n en este punto. Con la densidad ($\rho$), se observa lo siguiente:
| $ v_s = \sqrt{\displaystyle\frac{2 \Delta p_s }{ \rho }}$ |
(ID 15710)
La diferencia de alturas, representada por la diferencia de altura ($\Delta h$), implica que la presi n en ambas columnas es diferente. En particular, la diferencia de presión ($\Delta p$) es una funci n de la densidad del líquido ($\rho_w$), la aceleración gravitacional ($g$) y la diferencia de altura ($\Delta h$), de la siguiente manera:
| $ \Delta p = \rho_w g \Delta h $ |
(ID 4345)
El principio de continuidad establece que el flujo en el primer punto, que es igual a la densidad de flujo 1 ($j_{s1}$) por la sección en el punto 1 ($S_1$), debe ser igual al flujo en el segundo punto, dado por la densidad de flujo 2 ($j_{s2}$) por la sección en el punto 2 ($S_2$), de lo que se deduce que:
| $ S_1 j_{s1} = S_2 j_{s2} $ |
(ID 4350)
Para el caso de un l quido no viscoso que fluye en forma laminar, la diferencia de presi n generada por la columna es:
| $ \Delta p = \rho_w g \Delta h $ |
lo que da lugar a un flujo de velocidad $v$ a trav s de un tubo seg n el principio de Bernoulli:
| $ \Delta p = - \rho \bar{v} \Delta v $ |
Dada la velocidad y el radio del tubo, podemos calcular el flujo, que se relaciona con el flujo dentro de la columna mediante la ley de continuidad. A su vez, esto se relaciona con la variaci n de la altura $h$, como se describe en:
| $ S\displaystyle\frac{dh}{dt} = \pi R^2 \sqrt{2gh}$ |
(ID 9882)
Si observamos la ecuaci n para el vaciado de una columna de l quido no viscoso:
| $ S\displaystyle\frac{dh}{dt} = \pi R^2 \sqrt{2gh}$ |
podemos condensar las constantes en una unidad de tiempo caracter stica:
| $ \tau_b = \displaystyle\frac{S}{\pi R^2}\sqrt{\displaystyle\frac{h_0}{g}}$ |
Este valor se convierte en el tiempo en el que la columna se vac a por completo y depende de la altura inicial.
(ID 14523)
La ecuaci n que describe la evoluci n de la columna de l quido viscoso que se est drenando es la siguiente:
| $ S\displaystyle\frac{dh}{dt} = \pi R^2 \sqrt{2gh}$ |
Podemos reescribir esta ecuaci n en t rminos del tiempo caracter stico:
| $ \tau_b = \displaystyle\frac{S}{\pi R^2}\sqrt{\displaystyle\frac{h_0}{g}}$ |
Luego, al realizar la integraci n, obtenemos:
| $ h = h_0\left(1-\displaystyle\frac{t}{\tau_b}\right)^2$ |
Donde $h_0$ representa la altura inicial.
(ID 14524)
ID:(1427, 0)
