Bernoulli mit hydrostatischem Druck
Storyboard 
Wenn wir ein Fluid ohne Viskosität und ohne Turbulenzen (laminares Strömung) betrachten, können wir annehmen, dass die Energie erhalten bleibt und mit der Flüssigkeit (oder dem Gas) fließt. In diesen Fällen erhalten wir eine Gleichung, die besagt, dass die Summe aus der Dichte der kinetischen Energie und der Dichte der potenziellen Energie konstant ist.
Dies ermöglicht es, zu berechnen, wie sich die Geschwindigkeit in Abhängigkeit von der Position entwickelt, solange der vorhandene Druck oder jedes vorhandene Kraftfeld bekannt ist.
Das einzige Problem ist, dass die meisten Medien eine relevante Viskosität aufweisen und daher dazu neigen, keine Turbulenzen aufzuweisen oder diese vernachlässigbar sind und der Fluss intrinsisch turbulent ist. Daher ist die Anwendung des Bernoulli-Gesetzes in diesem Sinne eingeschränkt oder vielmehr eine erste Näherung.
ID:(684, 0)
Parfümspender
Audio 
In Parfümdispensern wird ein Luftstrom über einem in das Parfüm eingetauchten Rohr erzeugt. Dadurch sinkt der Druck, sodass der Druck in der Parfümsäule geringer ist als der Druck in der Flüssigkeitssäule innerhalb der Flasche. Dies bewirkt, dass die Flüssigkeit durch die Säule nach oben gedrückt wird. Schließlich wird die Flüssigkeit an der Spitze zerstäubt und mit dem Luftstrom wegtransportiert.
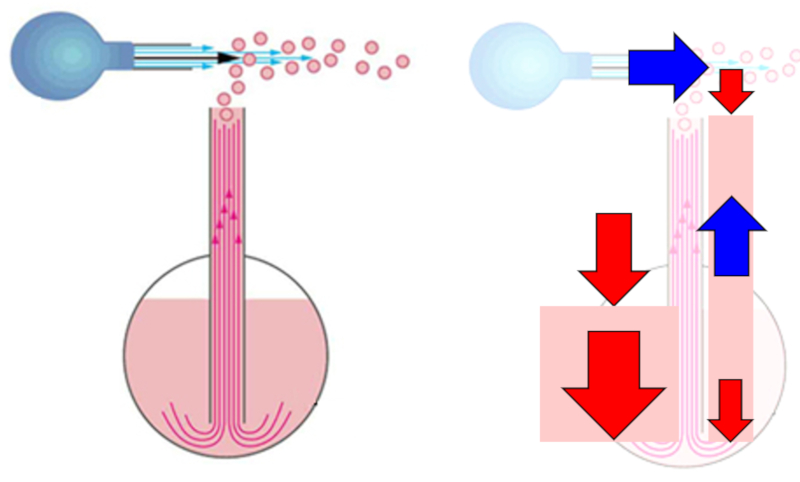
Um das System zu modellieren, kann das Bernoulli-Prinzip mit der Dichte der Flüssigkeit die Flüssigkeitsdichte ($\rho_w$) und der Höhe die Gravitationsbeschleunigung ($g$) verwendet werden. Wenn Punkt 1 sich am Boden des Flüssigkeitstransportrohrs befindet, dann ist die Mittlere Geschwindigkeit der Flüssigkeit in Punkt 1 ($v_1$) null, die Höhe oder Tiefe 1 ($h_1$) repräsentiert die Tiefe der Flüssigkeit ($h$), und die Druck in Spalte 1 ($p_1$) steht für den atmosphärischen Druck. Wenn Punkt 2 am oberen Auslass des Flüssigkeitstransportrohrs liegt, dann steht die Die mittlere Geschwindigkeit der Flüssigkeit in Punkt 2 ($v_2$) für die Geschwindigkeit, mit der die Flüssigkeit austritt ($v$), die Höhe oder Tiefe 2 ($h_2$) ist null, und die Druck in Spalte 2 ($p_2$) ist der atmosphärische Druck. Daher reduziert sich der Ausdruck
| $\displaystyle\frac{1}{2} \rho v_1 ^2+ \rho g h_1 + p_1 =\displaystyle\frac{1}{2} \rho v_2 ^2+ \rho g h_2 + p_2 $ |
zu
$\rho g h=\displaystyle\frac{1}{2}\rho v^2 $
da sich der atmosphärische Druck vereinfacht. Somit ergibt sich die Geschwindigkeit, mit der die Flüssigkeit austritt, zu:
$v = \sqrt{ 2 g h }$
ID:(11096, 0)
Bernoulli mit hydrostatischem Druck
Beschreibung 
Wenn wir ein Fluid ohne Viskosität und ohne Turbulenzen (laminares Strömung) betrachten, können wir annehmen, dass die Energie erhalten bleibt und mit der Flüssigkeit (oder dem Gas) fließt. In diesen Fällen erhalten wir eine Gleichung, die besagt, dass die Summe aus der Dichte der kinetischen Energie und der Dichte der potenziellen Energie konstant ist. Dies ermöglicht es, zu berechnen, wie sich die Geschwindigkeit in Abhängigkeit von der Position entwickelt, solange der vorhandene Druck oder jedes vorhandene Kraftfeld bekannt ist. Das einzige Problem ist, dass die meisten Medien eine relevante Viskosität aufweisen und daher dazu neigen, keine Turbulenzen aufzuweisen oder diese vernachlässigbar sind und der Fluss intrinsisch turbulent ist. Daher ist die Anwendung des Bernoulli-Gesetzes in diesem Sinne eingeschränkt oder vielmehr eine erste Näherung.
Variablen
Berechnungen
Berechnungen
Gleichungen
Eine weitere n tzliche Gleichung ist diejenige, die der Energieerhaltung entspricht und in F llen angewendet wird, in denen die Viskosit t vernachl ssigt werden kann, da sie einen Prozess darstellt, bei dem Energie verloren geht. Wenn wir die klassische Energiegleichung $E$ betrachten, die die kinetische Energie, die potenzielle Gravitationsenergie und eine u ere Kraft, die die Fl ssigkeit ber eine Strecke $\Delta z$ verschiebt, ber cksichtigt, kann sie wie folgt ausgedr ckt werden:
$E=\displaystyle\frac{m}{2}v^2+mgh+F\Delta x$
Wenn wir die Energie innerhalb eines Volumens $\Delta x\Delta y\Delta z$ betrachten, k nnen wir die Masse ersetzen durch:
$m=\rho \Delta x\Delta y\Delta z$
Und da der Druck gegeben ist durch:
$F=p \Delta S =p \Delta y\Delta z$
erhalten wir die Gleichung f r die Energiedichte:
| $ e =\displaystyle\frac{1}{2} \rho v ^2+ \rho g h + p $ |
(ID 3159)
Eine weitere n tzliche Gleichung ist diejenige, die der Energieerhaltung entspricht und in F llen angewendet wird, in denen die Viskosit t vernachl ssigt werden kann, da sie einen Prozess darstellt, bei dem Energie verloren geht. Wenn wir die klassische Energiegleichung $E$ betrachten, die die kinetische Energie, die potenzielle Gravitationsenergie und eine u ere Kraft, die die Fl ssigkeit ber eine Strecke $\Delta z$ verschiebt, ber cksichtigt, kann sie wie folgt ausgedr ckt werden:
$E=\displaystyle\frac{m}{2}v^2+mgh+F\Delta x$
Wenn wir die Energie innerhalb eines Volumens $\Delta x\Delta y\Delta z$ betrachten, k nnen wir die Masse ersetzen durch:
$m=\rho \Delta x\Delta y\Delta z$
Und da der Druck gegeben ist durch:
$F=p \Delta S =p \Delta y\Delta z$
erhalten wir die Gleichung f r die Energiedichte:
| $ e =\displaystyle\frac{1}{2} \rho v ^2+ \rho g h + p $ |
(ID 3159)
(ID 4252)
Wenn zwischen zwei Punkten die Druckunterschied ($\Delta p$) existiert, wie durch die Gleichung bestimmt:
| $ dp = p - p_0 $ |
k nnen wir die Druck der Wassersäule ($p$) verwenden, definiert als:
| $ p_t = p_0 + \rho_w g h $ |
Dies ergibt:
$\Delta p=p_2-p_1=p_0+\rho_wh_2g-p_0-\rho_wh_1g=\rho_w(h_2-h_1)g$
Da die Höhendifferenz ($\Delta h$) wie folgt definiert ist:
| $ \Delta h = h_2 - h_1 $ |
kann die Druckunterschied ($\Delta p$) wie folgt ausgedr ckt werden:
| $ \Delta p = \rho_w g \Delta h $ |
(ID 4345)
Angenommen, dass die Energiedichte ($e$) erhalten bleibt, k nnen wir feststellen, dass f r eine Zelle, in der die Durchschnittsgeschwindigkeit die Geschwindigkeit auf einer Zylinder-Radio ($v$) betr gt, die Dichte die Dichte ($\rho$), der Druck die Druck der Wassersäule ($p$), die H he die Höhe der Säule ($h$) und die Gravitationsbeschleunigung die Gravitationsbeschleunigung ($g$) folgendes gilt:
| $ e =\displaystyle\frac{1}{2} \rho v ^2+ \rho g h + p $ |
An Punkt 1 wird diese Gleichung gleich der gleichen Gleichung an Punkt 2 sein:
$e(v_1,p_1,h_1)=e(v_2,p_2,h_2)$
wobei die Mittlere Geschwindigkeit der Flüssigkeit in Punkt 1 ($v_1$), die Höhe oder Tiefe 1 ($h_1$) und die Druck in Spalte 1 ($p_1$) die Geschwindigkeit, H he und Druck an Punkt 1 darstellen und die Die mittlere Geschwindigkeit der Flüssigkeit in Punkt 2 ($v_2$), die Höhe oder Tiefe 2 ($h_2$) und die Druck in Spalte 2 ($p_2$) die Geschwindigkeit, H he und Druck an Punkt 2 darstellen. Daher haben wir:
| $\displaystyle\frac{1}{2} \rho v_1 ^2+ \rho g h_1 + p_1 =\displaystyle\frac{1}{2} \rho v_2 ^2+ \rho g h_2 + p_2 $ |
(ID 4504)
(ID 15499)
(ID 15502)
Beispiele
(ID 15486)
Wenn wir den Fluss als eine Reihe von Volumina mit den Seitenl ngen $\Delta x$, $\Delta y$ und $\Delta z$ betrachten, die sich in der Str mung bewegen, k nnen wir annehmen, dass die darin enthaltene Energie konstant bleibt. Dies bedeutet, dass die berechnete Energie-Dichte an jedem Punkt immer gleich sein wird.
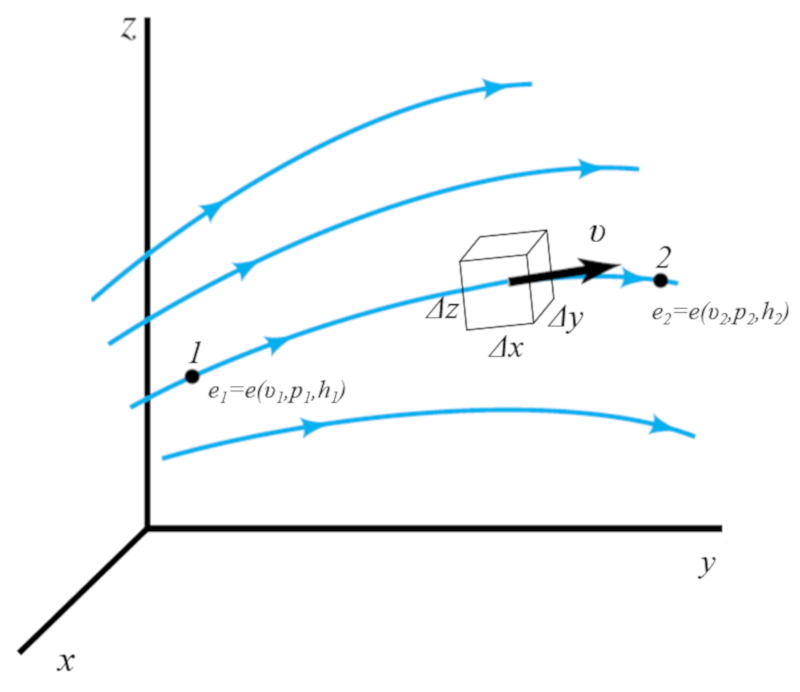
(ID 11097)
Wenn das Medium eine Dichte von $\rho$ aufweist, kann die Masse des Volumens $\Delta x\Delta y\Delta z$ berechnet werden als:
$m=\rho\Delta x\Delta y\Delta z$
Daraus k nnen wir die kinetische Energie des Elements unter Verwendung der Geschwindigkeit $v$ absch tzen:
$\displaystyle\frac{1}{2}m v^2=\displaystyle\frac{1}{2}\rho\Delta x\Delta y\Delta z v^2$
Dies kann in folgender Abbildung visualisiert werden:
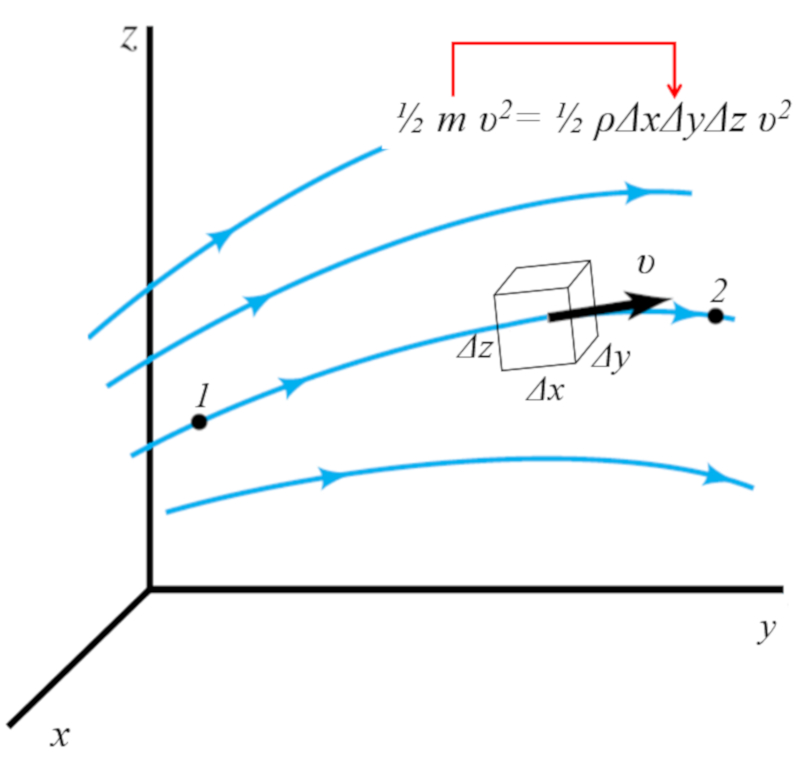
Daher betr gt die Dichte der kinetischen Energie
$\displaystyle\frac{m v^2}{2 \Delta x\Delta y\Delta z}=\displaystyle\frac{1}{2}\rho v^2$
(ID 11101)
Wenn das Medium eine Dichte von $\rho$ hat, kann die Masse des Volumens $\Delta x\Delta y\Delta z$ berechnet werden als
$m=\rho\Delta x\Delta y\Delta z$
mit dem, was Sie mit der H he $h$ der potentiellen Gravitationsenergie des Elements absch tzen k nnen
$mgh=\rho\Delta x\Delta y\Delta z gh$
was wird in angezeigt
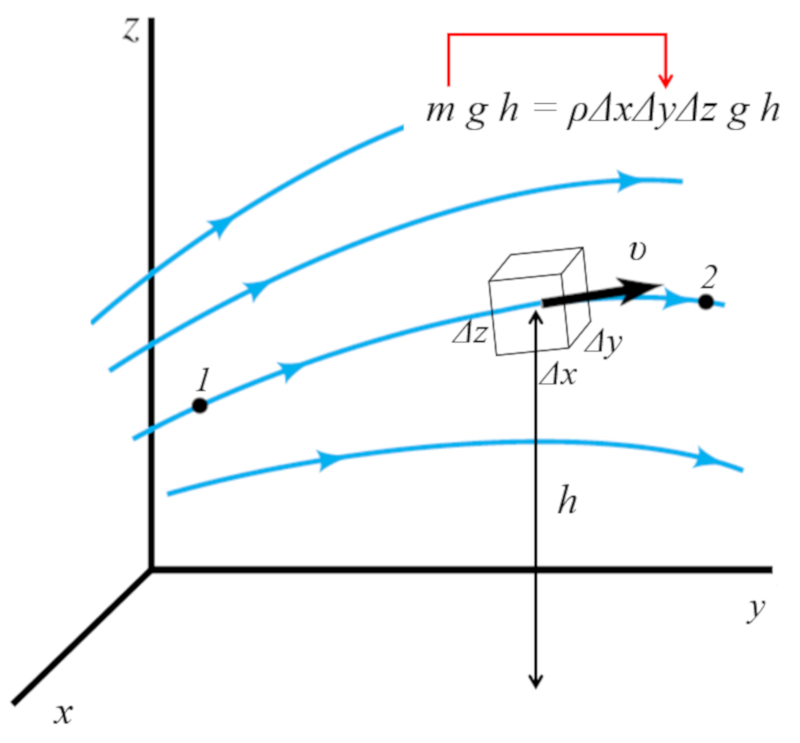
Daher betr gt die Dichte der potentiellen Gravitationsenergie
$\displaystyle\frac{mgh}{\Delta x\Delta y\Delta z}=\rho g h$
(ID 11102)
Wenn wir davon ausgehen, dass eine Kraft auf das Element wirkt und das Koordinatensystem so orientieren, dass diese Kraft in Richtung der x-Achse wirkt, dann wird die Kraft Arbeit leisten:
$F\Delta x$
Wenn die Kraft durch einen Druck erzeugt wird, dann wirkt die Kraft auf die Fl che senkrecht zur Richtung der Kraft, also $\Delta y \Delta z$. Somit ergibt sich die Energie zu:
$F = p \Delta S = p \Delta y\Delta z$
Dies kann in der folgenden Abbildung visualisiert werden:
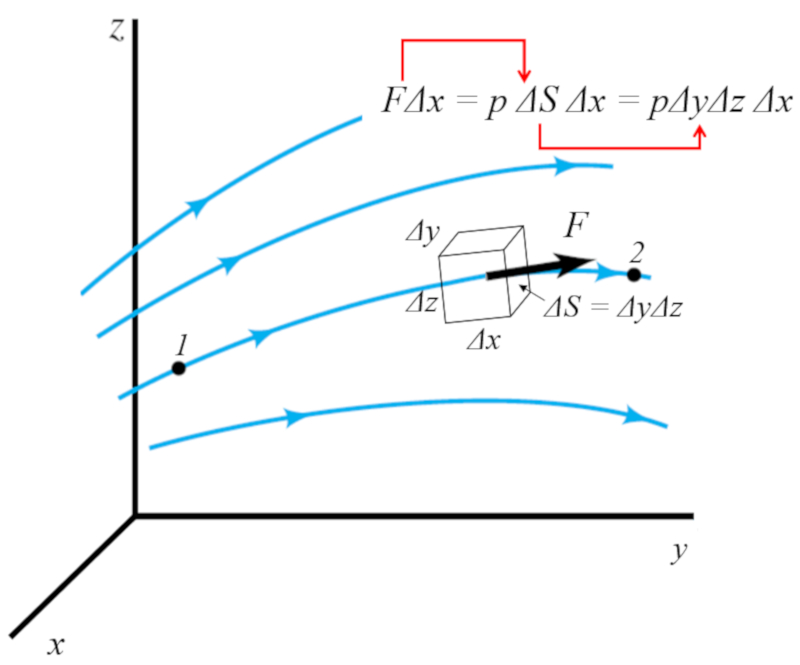
Daher ist die Dichte der allgemeinen Energie
$\displaystyle\frac{F \Delta x}{\Delta x\Delta y\Delta z}=\displaystyle\frac{p \Delta x\Delta y\Delta z}{\Delta x\Delta y\Delta z}=p$
(ID 11103)
Die Bernoulli-Hypothese besagt, dass Energie lokal erhalten bleibt, was bedeutet, dass es keine Mechanismen gibt, die es einem Volumen des Mediums erm glichen, Energie mit seiner Umgebung auszutauschen. Wenn wir die Energiegleichung $E$ betrachten, die Folgendes umfasst:
• Die kinetische Energie als Funktion der Masse $m$ und der Geschwindigkeit die Geschwindigkeit auf einer Zylinder-Radio ($v$),
• Die potenzielle Gravitationsenergie als Funktion von die Gravitationsbeschleunigung ($g$) und die Höhe der Säule ($h$) und
• Eine externe Kraft $F$, die die Fl ssigkeit um eine Entfernung $\Delta z$ verschiebt,
k nnen wir sie wie folgt ausdr cken:
$E=\displaystyle\frac{m}{2}v^2+mgh+F\Delta x$
Wenn wir die Energie in einem Volumen $\Delta x\Delta y\Delta z$ betrachten, k nnen wir die Masse durch die Dichte ($\rho$) ersetzen:
$m=\rho \Delta x\Delta y\Delta z$
Und da die Druck der Wassersäule ($p$) wie folgt ausgedr ckt wird:
$F=p \Delta S =p \Delta y\Delta z$
erhalten wir die Gleichung f r die Energiedichte ($e$):
| $ e =\displaystyle\frac{1}{2} \rho v ^2+ \rho g h + p $ |
In Abwesenheit von Viskosit t impliziert die Energieerhaltung, dass die Energiedichte ($e$) an jeder Stelle im Fluid konstant ist. Daher reicht es aus, die Geschwindigkeit und/oder den Druck an jeder Stelle im Fluid zu kennen, um eine Beziehung zwischen Geschwindigkeit und Druck an jeder Stelle im Fluid herzustellen.
(ID 15708)
Die Hypothese des Bernoulli-Gesetzes besagt, dass die Energie, und somit auch die Energiedichte ($e$), konstant bleibt. In diesem Fall ist die Energiedichte die Summe aus:
• Kinetischer Energie, die von die Flüssigkeitsdichte ($\rho_w$) und die Geschwindigkeit auf einer Zylinder-Radio ($v$) abh ngt,
• Gravitationspotenzieller Energie, die von die Gravitationsbeschleunigung ($g$) und die Höhe der Säule ($h$) abh ngt,
• Allgemeiner potenzieller Energie, die von die Druck ($p$) abh ngt,
resultierend in:
| $ e =\displaystyle\frac{1}{2} \rho v ^2+ \rho g h + p $ |
Dies beschr nkt jedoch die Anwendbarkeit des Gesetzes, da:
• Viskosit t ein Prozess ist, bei dem Energie durch das Medium diffundiert, und in diesem Sinne wird Energie lokal nicht erhalten, da sie sich im Medium neu verteilt.
• Wirbel k nnen nicht existieren, da sie inh rent Zonen unterschiedlicher Energiedichten aufweisen, was der Hypothese widerspricht. Dies bedeutet, dass es keinen turbulenten Fluss beschreiben w rde.
Das Problem besteht darin, dass in den meisten F llen der Fluss von Viskosit t dominiert werden kann, was als laminarer Fluss bezeichnet wird, oder von Tr gheit dominiert wird, was zu turbulentem Fluss f hrt. Daher ist das Bernoulli-Gesetz nur in Situationen anwendbar, in denen die Inhomogenit t der Energiedichte geringer ist.
(ID 15500)
Angenommen, dass die Energiedichte ($e$) erhalten bleibt, k nnen wir feststellen, dass f r eine Zelle, in der die Durchschnittsgeschwindigkeit die Geschwindigkeit auf einer Zylinder-Radio ($v$) betr gt, die Dichte die Dichte ($\rho$), der Druck die Druck der Wassersäule ($p$), die H he die Höhe der Säule ($h$) und die Gravitationsbeschleunigung die Gravitationsbeschleunigung ($g$) folgendes gilt:
| $ e =\displaystyle\frac{1}{2} \rho v ^2+ \rho g h + p $ |
An Punkt 1 wird diese Gleichung gleich der gleichen Gleichung an Punkt 2 sein:
$e(v_1,p_1,h_1)=e(v_2,p_2,h_2)$
wobei die Mittlere Geschwindigkeit der Flüssigkeit in Punkt 1 ($v_1$), die Höhe oder Tiefe 1 ($h_1$) und die Druck in Spalte 1 ($p_1$) die Geschwindigkeit, H he und Druck an Punkt 1 darstellen und die Die mittlere Geschwindigkeit der Flüssigkeit in Punkt 2 ($v_2$), die Höhe oder Tiefe 2 ($h_2$) und die Druck in Spalte 2 ($p_2$) die Geschwindigkeit, H he und Druck an Punkt 2 darstellen.
Daher haben wir die Bernoulli-Gleichung [1]:
| $\displaystyle\frac{1}{2} \rho v_1 ^2+ \rho g h_1 + p_1 =\displaystyle\frac{1}{2} \rho v_2 ^2+ \rho g h_2 + p_2 $ |
![]() [1] "Hydrodynamica" (Hidrodinamica), Daniel Bernoulli, Typis Joh. Henr. Deckeri (1738)
[1] "Hydrodynamica" (Hidrodinamica), Daniel Bernoulli, Typis Joh. Henr. Deckeri (1738)
Es ist wichtig, folgende Annahmen zu beachten:
Die Energie bleibt erhalten, insbesondere wird die Abwesenheit von Viskosit t angenommen.
Es gibt keine Verformung des Mediums, wodurch die Dichte konstant bleibt.
Es gibt keine Wirbelbildung (Vortizit t), das hei t, es gibt keine Strudelbewegungen, die zu Zirkulation im Medium f hren. Die Fl ssigkeit muss ein laminarisches Verhalten aufweisen.
(ID 15707)
In Parf mdispensern wird ein Luftstrom ber einem in das Parf m eingetauchten Rohr erzeugt. Dadurch sinkt der Druck, sodass der Druck in der Parf ms ule geringer ist als der Druck in der Fl ssigkeitss ule innerhalb der Flasche. Dies bewirkt, dass die Fl ssigkeit durch die S ule nach oben gedr ckt wird. Schlie lich wird die Fl ssigkeit an der Spitze zerst ubt und mit dem Luftstrom wegtransportiert.

Um das System zu modellieren, kann das Bernoulli-Prinzip mit der Dichte der Fl ssigkeit die Flüssigkeitsdichte ($\rho_w$) und der H he die Gravitationsbeschleunigung ($g$) verwendet werden. Wenn Punkt 1 sich am Boden des Fl ssigkeitstransportrohrs befindet, dann ist die Mittlere Geschwindigkeit der Flüssigkeit in Punkt 1 ($v_1$) null, die Höhe oder Tiefe 1 ($h_1$) repr sentiert die Tiefe der Fl ssigkeit ($h$), und die Druck in Spalte 1 ($p_1$) steht f r den atmosph rischen Druck. Wenn Punkt 2 am oberen Auslass des Fl ssigkeitstransportrohrs liegt, dann steht die Die mittlere Geschwindigkeit der Flüssigkeit in Punkt 2 ($v_2$) f r die Geschwindigkeit, mit der die Fl ssigkeit austritt ($v$), die Höhe oder Tiefe 2 ($h_2$) ist null, und die Druck in Spalte 2 ($p_2$) ist der atmosph rische Druck. Daher reduziert sich der Ausdruck
| $\displaystyle\frac{1}{2} \rho v_1 ^2+ \rho g h_1 + p_1 =\displaystyle\frac{1}{2} \rho v_2 ^2+ \rho g h_2 + p_2 $ |
zu
$\rho g h=\displaystyle\frac{1}{2}\rho v^2 $
da sich der atmosph rische Druck vereinfacht. Somit ergibt sich die Geschwindigkeit, mit der die Fl ssigkeit austritt, zu:
$v = \sqrt{ 2 g h }$
(ID 11096)
(ID 15489)
ID:(684, 0)
