Storyboard

En el caso de que el flujo ocurra en un gas o en una situación en la que las variaciones de la altura sean mínimas, se puede despreciar el efecto de la presión hidrostática.

Sin la presión hidrostática, la ley de Bernoulli se reduce a que la suma de un término asociado a la energía cinética, y por ende a la velocidad al cuadrado, y la presión que existe en cada lugar, se mantiene constante. Esto significa que si la velocidad aumenta, la presión disminuye, y viceversa.

>Modelo

ID:(2066, 0)

Concepto

>Top

ID:(15497, 0)

Concepto

>Top

Si la energía se conserva y el medio fluye sin deformarse, se cumple que la densidad entre dos puntos debe ser igual, lo que es la premisa que lleva a la ley de Bernoulli.

Como la densidad de energía se calcula en un punto 1 y 2 de:
• la densidad de energía científica depende de la densidad del líquido ($\rho_w$) y en el punto 1 de la velocidad media del fluido en el punto 1 ($v_1$) y en el punto 2 de la velocidad media del fluido en el punto 2 ($v_2$)
• la densidad de energía potencial en general que corresponde en el punto 1 a la presión en la columna 1 ($p_1$) y la presión en la columna 2 ($p_2$)
se tiene la relación

Esta expresión se puede reescribir con el diferencial de la presión ($\Delta p$)

con la velocidad promedio ($\bar{v}$)

y con la diferencia de velocidad entre superficies ($\Delta v$)

se tiene finalmente

ID:(15503, 0)

Descripción

>Top

Los aviones determinan la velocidad utilizando el llamado tubo de Pitot. Este tubo consta de dos orificios, uno en el frente (borde de ataque) y el otro en uno de los lados. En el borde de ataque, la velocidad es nula, mientras que en el lateral se registra la velocidad a la que el avión avanza con respecto al medio. En las aberturas del tubo, se encuentran dos conductos que contienen un líquido para medir la diferencia de presión entre ambos puntos. Utilizando la ecuación de Bernoulli, es posible calcular la velocidad del avión a partir de la diferencia de presión y la densidad del líquido.

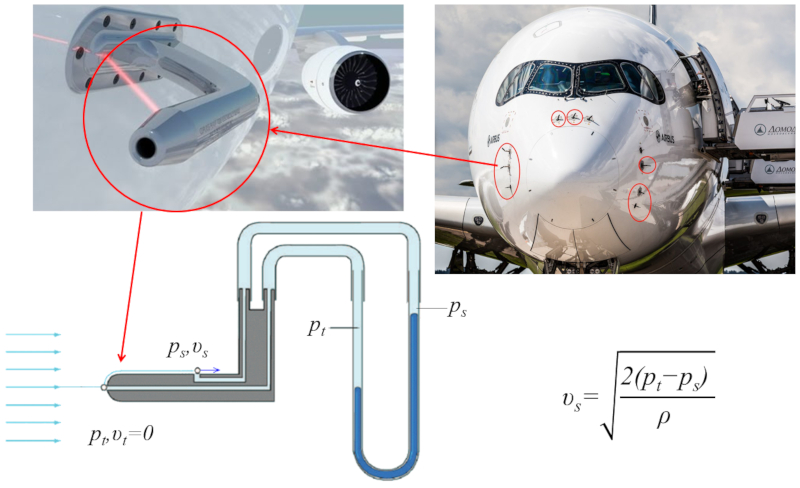
El funcionamiento del tubo de Pitot se modela el diferencial de la presión ($\Delta p$) con la velocidad promedio ($\bar{v}$) y la diferencia de velocidad entre superficies ($\Delta v$) con la densidad ($\rho$) mediante

En particular, la velocidad en la punta del tubo de Pitot es nula, lo que hace que la diferencia de velocidad entre superficies ($\Delta v$) se reduzca a la velocidad en el orificio lateral ($\Delta v = v$), mientras que la velocidad promedio ($\bar{v}$) es igual a la mitad de la velocidad ($\bar{v}=v/2$). Dado que la velocidad corresponde a la velocidad del avión, esta puede determinarse midiendo la presión mediante la ecuación

$v=\sqrt{\displaystyle\frac{2 \Delta p}{\rho}}$

Es importante tener en cuenta que esta ecuación requiere la densidad, que varía con la altura a la que vuela el avión.

ID:(11095, 0)

Descripción

>Top

Cuando se adelanta a un automóvil en la carretera, se crea una situación en la que se genera un flujo de aire de mayor velocidad entre los dos vehículos, lo que implica que en esa zona la presión será menor. Como resultado, la presión en los lados exteriores de los automóviles hará que se atraigan mutuamente.

Cuando los vehículos se cruzan, la velocidad relativa entre ellos disminuirá y se acercará al reposo, generando una mayor presión entre ellos que tenderá a alejar los vehículos el uno del otro.

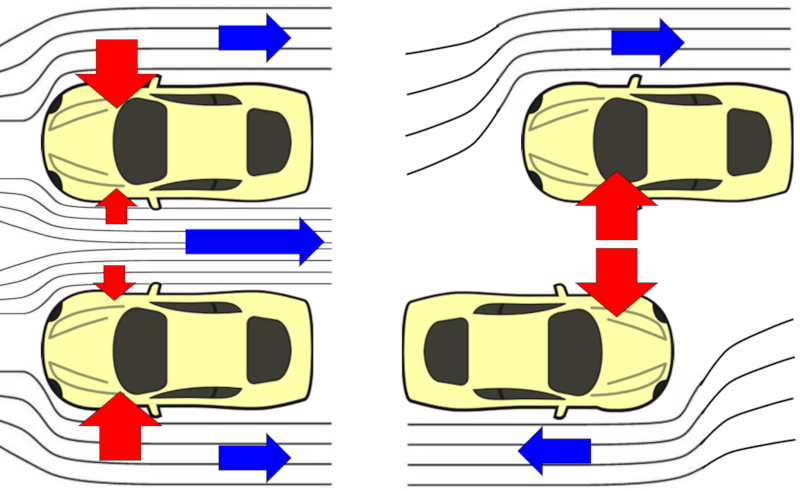
Lo mismo ocurre cuando dos barcos se cruzan. Si el cruce se produce en un canal angosto, ambos timoneles deberán dirigir sus naves hacia el lado opuesto para evitar que la fuerza repulsiva provoque un choque con el borde del canal.

Para explicar por qué ocurre esto, se puede aplicar la ecuación de el diferencial de la presión ($\Delta p$) con la velocidad promedio ($\bar{v}$) y la diferencia de velocidad entre superficies ($\Delta v$) con la densidad ($\rho$) mediante

Por lo tanto, se observa que si hay un gradiente en la velocidad, este es inverso al de la presión. Si uno aumenta, el otro disminuye, lo que explica que al rebasar los autos presenten una mayor velocidad entre ellos, lo que lleva a una reducción de la presión entre ambos, succionándolos mutuamente. A la inversa, si se cruzan, la velocidad entre ambos es aproximadamente nula, lo que genera un gradiente de presión que los aleja mutuamente.

ID:(11094, 0)

Concepto

>Top

Parámetro seleccionado

Cálculos

ID:(15498, 0)

Ecuación

>Top, >Modelo

Dado que un fluido o gas es un continuo, el concepto de energía ya no puede asociarse a una masa específica. Sin embargo, es posible considerar la energía contenida en un volumen del continuo y, al dividirla por el volumen mismo, se obtiene la densidad de energía ($e$). Por lo tanto, con la densidad ($\rho$), la velocidad media del fluido ($v$) y la presión de la columna de agua ($p_t$), tenemos:

$ e =\displaystyle\frac{1}{2} \rho v ^2+ p $

Condiciones

Variables

$\rho$

Densidad

$kg/m^3$

$e$

Densidad de energía

$J/m^3$

$p$

Presión de la columna de agua

$Pa$

$v$

Velocidad media del fluido

$m/s$

Relación

Desarrollo

Otra ecuación útil es la que corresponde a la conservación de energía, que se aplica en casos donde la viscosidad, un proceso en el cual se pierde energía, puede ser despreciada. Si consideramos la clásica ecuación de energía $E$, que incluye la energía cinética, la energía potencial gravitacional y una fuerza externa que desplaza el líquido una distancia $\Delta z$, podemos expresarla de la siguiente manera:

$E=\displaystyle\frac{m}{2}v^2+mgh+F\Delta x$

Si consideramos la energía en un volumen $\Delta x\Delta y\Delta z$, podemos reemplazar la masa por:

$m=\rho \Delta x\Delta y\Delta z$

Y como la presión se expresa como:

$F=p \Delta S =p \Delta y\Delta z$

Obtenemos la ecuación de densidad de energía:

$ e =\displaystyle\frac{1}{2} \rho v ^2+ p $

que corresponde a la ecuación de Bernoulli.

En ausencia de viscosidad, la conservación de energía implica que la densidad de energía ($e$) es constante en cualquier punto del fluido. Por lo tanto, conocer la velocidad y/o la presión en cualquier lugar del fluido es suficiente para establecer una relación entre la velocidad y la presión en cualquier punto del fluido.

ID:(15496, 0)

Ecuación

>Top, >Modelo

Si la energía se conserva dentro de los volúmenes que fluyen con el flujo, entonces la densidad de energía en 1 ($e_1$) y la densidad de energía en 2 ($e_2$) deben ser iguales:

$ e_1 = e_2 $

Condiciones

Variables

$e_1$

Densidad de energía en 1

$J/m^3$

$e_2$

Densidad de energía en 2

$J/m^3$

Relación

Esto solo es posible si la viscosidad es despreciable, ya que esta está asociada a la difusión de energía y no existen torbellinos, los cuales presentan diferencias de energía debido a las velocidades tangenciales variadas a lo largo del radio del vórtice.

ID:(15499, 0)

Ecuación

>Top, >Modelo

Dado que un fluido o gas es un continuo, el concepto de energía ya no puede asociarse a una masa específica. Sin embargo, es posible considerar la energía contenida en un volumen del continuo y, al dividirla por el volumen mismo, se obtiene la densidad de energía ($e$). Por lo tanto, con la densidad ($\rho$), la velocidad media del fluido ($v$) y la presión de la columna de agua ($p_t$), tenemos:

$ e_1 =\displaystyle\frac{1}{2} \rho v_1 ^2+ p_1 $

$ e =\displaystyle\frac{1}{2} \rho v ^2+ p $

Condiciones

Variables

$\rho$

Densidad

$kg/m^3$

$e$

$e_1$

Densidad de energía en 1

$J/m^3$

$p$

$p_1$

Presión en la columna 1

$Pa$

$v$

$v_1$

Velocidad media del fluido en el punto 1

$m/s$

Relación

Desarrollo

Otra ecuación útil es la que corresponde a la conservación de energía, que se aplica en casos donde la viscosidad, un proceso en el cual se pierde energía, puede ser despreciada. Si consideramos la clásica ecuación de energía $E$, que incluye la energía cinética, la energía potencial gravitacional y una fuerza externa que desplaza el líquido una distancia $\Delta z$, podemos expresarla de la siguiente manera:

$E=\displaystyle\frac{m}{2}v^2+mgh+F\Delta x$

Si consideramos la energía en un volumen $\Delta x\Delta y\Delta z$, podemos reemplazar la masa por:

$m=\rho \Delta x\Delta y\Delta z$

Y como la presión se expresa como:

$F=p \Delta S =p \Delta y\Delta z$

Obtenemos la ecuación de densidad de energía:

$ e =\displaystyle\frac{1}{2} \rho v ^2+ p $

que corresponde a la ecuación de Bernoulli.

En ausencia de viscosidad, la conservación de energía implica que la densidad de energía ($e$) es constante en cualquier punto del fluido. Por lo tanto, conocer la velocidad y/o la presión en cualquier lugar del fluido es suficiente para establecer una relación entre la velocidad y la presión en cualquier punto del fluido.

ID:(15496, 1)

Ecuación

>Top, >Modelo

Dado que un fluido o gas es un continuo, el concepto de energía ya no puede asociarse a una masa específica. Sin embargo, es posible considerar la energía contenida en un volumen del continuo y, al dividirla por el volumen mismo, se obtiene la densidad de energía ($e$). Por lo tanto, con la densidad ($\rho$), la velocidad media del fluido ($v$) y la presión de la columna de agua ($p_t$), tenemos:

$ e_2 =\displaystyle\frac{1}{2} \rho v_2 ^2+ p_2 $

$ e =\displaystyle\frac{1}{2} \rho v ^2+ p $

Condiciones

Variables

$\rho$

Densidad

$kg/m^3$

$e$

$e_2$

Densidad de energía en 2

$J/m^3$

$p$

$p_2$

Presión en la columna 2

$Pa$

$v$

$v_2$

Velocidad media del fluido en el punto 2

$m/s$

Relación

Desarrollo

Otra ecuación útil es la que corresponde a la conservación de energía, que se aplica en casos donde la viscosidad, un proceso en el cual se pierde energía, puede ser despreciada. Si consideramos la clásica ecuación de energía $E$, que incluye la energía cinética, la energía potencial gravitacional y una fuerza externa que desplaza el líquido una distancia $\Delta z$, podemos expresarla de la siguiente manera:

$E=\displaystyle\frac{m}{2}v^2+mgh+F\Delta x$

Si consideramos la energía en un volumen $\Delta x\Delta y\Delta z$, podemos reemplazar la masa por:

$m=\rho \Delta x\Delta y\Delta z$

Y como la presión se expresa como:

$F=p \Delta S =p \Delta y\Delta z$

Obtenemos la ecuación de densidad de energía:

$ e =\displaystyle\frac{1}{2} \rho v ^2+ p $

que corresponde a la ecuación de Bernoulli.

En ausencia de viscosidad, la conservación de energía implica que la densidad de energía ($e$) es constante en cualquier punto del fluido. Por lo tanto, conocer la velocidad y/o la presión en cualquier lugar del fluido es suficiente para establecer una relación entre la velocidad y la presión en cualquier punto del fluido.

ID:(15496, 2)

Ecuación

>Top, >Modelo

En el caso de la ley de Bernoulli [1] para el caso que no exista presión hidrostatica se tiene que con la densidad ($\rho$), la presión en la columna 1 ($p_1$), la presión en la columna 2 ($p_2$), la velocidad media del fluido en el punto 1 ($v_1$) y la velocidad media del fluido en el punto 2 ($v_2$):

$\displaystyle\frac{1}{2} \rho v_1 ^2 + p_1 =\displaystyle\frac{1}{2} \rho v_2 ^2 + p_2 $

Condiciones

Variables

$\rho$

Densidad

$kg/m^3$

$p_1$

Presión en la columna 1

$Pa$

$p_2$

Presión en la columna 2

$Pa$

$v_1$

Velocidad media del fluido en el punto 1

$m/s$

$v_2$

Velocidad media del fluido en el punto 2

$m/s$

Relación

La ecuación de Bernoulli asume que se conserva la densidad de energía, lo que implica la ausencia de viscosidad y turbulencia, por lo que su aplicación en este caso es limitada.

La ecuación de Bernoulli puede ser utilizada como base para modelar el proceso, pero debe ser complementada con un modelo que considere la posibilidad de incluir el efecto de la turbulencia.

[1] "Hydrodynamica" (Hidrodinamica), Daniel Bernoulli, Typis Joh. Henr. Deckeri (1738)

ID:(15495, 0)

Ecuación

>Top, >Modelo

Cuando se conectan dos columnas de líquido con la presión en la columna 1 ($p_1$) y la presión en la columna 2 ($p_2$), se crea una la diferencia de presión ($\Delta p$) que se calcula mediante la siguiente fórmula:

$ \Delta p = p_2 - p_1 $

Condiciones

Variables

$\Delta p$

Diferencial de la presión

$Pa$

$p_1$

Presión en la columna 1

$Pa$

$p_2$

Presión en la columna 2

$Pa$

Relación

la diferencia de presión ($\Delta p$) representa la diferencia de presiones que desplazará el líquido de la columna más alta hacia la columna más baja.

ID:(4252, 0)

Ecuación

>Top, >Modelo

La velocidad promedio ($\bar{v}$) es con la velocidad media del fluido en el punto 1 ($v_1$) y la velocidad media del fluido en el punto 2 ($v_2$) es

$ \bar{v} = \displaystyle\frac{ v_1 + v_2 }{2}$

Condiciones

Variables

$v_1$

Velocidad media del fluido en el punto 1

$m/s$

$v_2$

Velocidad media del fluido en el punto 2

$m/s$

$\bar{v}$

Velocidad promedio

$m/s$

Relación

ID:(15501, 0)

Ecuación

>Top, >Modelo

La diferencia de velocidad entre superficies ($\Delta v$) es con la velocidad media del fluido en el punto 1 ($v_1$) y la velocidad media del fluido en el punto 2 ($v_2$) es

$ \Delta v = v_2 - v_1 $

Condiciones

Variables

$\Delta v$

Diferencia de velocidad entre superficies

$m/s$

$v_1$

Velocidad media del fluido en el punto 1

$m/s$

$v_2$

Velocidad media del fluido en el punto 2

$m/s$

Relación

ID:(15502, 0)

Ecuación

>Top, >Modelo

El diferencial de la presión ($\Delta p$) se puede calcular de la velocidad promedio ($\bar{v}$) y la diferencia de velocidad entre superficies ($\Delta v$) con la densidad ($\rho$) mediante

$ \Delta p = - \rho \bar{v} \Delta v $

Condiciones

Variables

$\rho$

Densidad

$kg/m^3$

$\Delta v$

Diferencia de velocidad entre superficies

$m/s$

$\Delta p$

Diferencial de la presión

$Pa$

$\bar{v}$

Velocidad promedio

$m/s$

Relación

Desarrollo

Para el caso de que no exista presión histrostatica la ley de Bernoulli para la densidad del líquido ($\rho_w$), la presión en la columna 1 ($p_1$), la presión en la columna 2 ($p_2$), la velocidad media del fluido en el punto 1 ($v_1$) y la velocidad media del fluido en el punto 2 ($v_2$)

$\displaystyle\frac{1}{2} \rho v_1 ^2 + p_1 =\displaystyle\frac{1}{2} \rho v_2 ^2 + p_2 $

se puede reescribir con el diferencial de la presión ($\Delta p$)

$ \Delta p = p_2 - p_1 $

y teniendo presente de que

$v_2^2 - v_1^2 = \displaystyle\frac{1}{2}(v_2-v_1)(v_1+v_2)$

con

$ \bar{v} = \displaystyle\frac{ v_1 + v_2 }{2}$

y

$ \Delta v = v_2 - v_1 $

se tiene que

$ \Delta p = - \rho \bar{v} \Delta v $

que permite ver el efecto de la melocidad promedio de un cuerpo y de la diferencia de esta entre sus superficies como se observa en un ala de avion o ave.

ID:(4835, 0)