Usuario:
Flexión elástica
Storyboard 
Cuando se aplica un torque a un cuerpo, se logra flexionarlo. La forma en que esto ocurre depende tanto de la geometría del cuerpo como de la manera en que se aplica el torque. Además, es posible estimar la energía elástica que el cuerpo absorbe en función de la deformación que experimenta.
ID:(2062, 0)
Doblando una viga
Imagen
Si se dobla una viga se observa que las secciones rotan en un ángulo
para lo que se requiere tensar usando cizalla (un par de tensiones opuestas).
ID:(14185, 0)
Flexión elástica
Modelo
Cuando se aplica un torque a un cuerpo, se logra flexionarlo. La forma en que esto ocurre depende tanto de la geometría del cuerpo como de la manera en que se aplica el torque. Además, es posible estimar la energía elástica que el cuerpo absorbe en función de la deformación que experimenta.
Variables
Cálculos
a 
,
luego, seleccione la variable: 
a 
Cálculos
Variable
Dado
Calcule
Objetivo :
Ecuación
A utilizar
Ecuaciones
Si se observa c mo var a la fuerza vertical al eje de la viga ($Q_z$) en funci n de la carga por largo sobre la viga ($q_z$) sobre un elemento de la posición a lo largo de la viga ($x$), se obtiene:
$Q - qdx - (Q + dQ) = 0$
por lo tanto:
$-qdx - dQ = 0$
lo que nos lleva a:
| $\displaystyle\frac{d Q_z }{dx} = - q_z $ |
(ID 15888)
La variaci n de el torque sobre la viga ($M_y$) a lo largo de la posición a lo largo de la viga ($x$) es del orden del brazo del largo del elemento la posición a lo largo de la viga ($x$) multiplicado por la fuerza vertical al eje de la viga ($Q_z$), por lo tanto:
$-M - Qdx + (M + dM) = 0$
lo que implica:
$-Qdx + dM = 0$
es decir:
| $\displaystyle\frac{d M_y }{d x } = Q_z $ |
(ID 15889)
Dado que el torque sobre la viga ($M_y$) derivado en la posición a lo largo de la viga ($x$) resulta en la fuerza vertical al eje de la viga ($Q_z$):
| $\displaystyle\frac{d M_y }{d x } = Q_z $ |
y la derivada de la fuerza vertical al eje de la viga ($Q_z$) es igual a menos la carga por largo sobre la viga ($q_z$):
| $\displaystyle\frac{d Q_z }{dx} = - q_z $ |
la derivada de la primera nos conduce a:
| $\displaystyle\frac{d^2 M_y }{d x ^2} = - q $ |
(ID 15890)
Si se observa c mo var a la fuerza axial en la viga ($N_x$) en funci n de la fuerza axial lor largo en la viga ($n$) sobre un elemento de la posición a lo largo de la viga ($x$), se obtiene:
$N - ndx - (N + dN) = 0$
por lo tanto:
$-ndx - dN = 0$
lo que nos lleva a:
| $\displaystyle\frac{d N_x }{d x } = - n $ |
(ID 15891)
Con el torque sobre la viga ($M_y$), la carga por largo sobre la viga ($q_z$) y la posición a lo largo de la viga ($x$), se establece la ecuaci n del torque:
| $\displaystyle\frac{d^2 M_y }{d x ^2} = - q $ |
que, junto con la ecuaci n del desplazamiento que involucra el módulo de Elasticidad ($E$), el momento de inercia de la sección ($I_b$) y el desplazamiento en z ($u_z$):
| $ M_y = - E I_b \displaystyle\frac{d^2 u_z }{d x ^2}$ |
nos lleva a:
| $ E I_b \displaystyle\frac{d^4 u_z }{d x ^4} = q_z $ |
(ID 15892)
Ejemplos
(ID 15570)
Si se aplica a un elemento de material torque se logra que este se flexiones en torno al eje de este mismo:
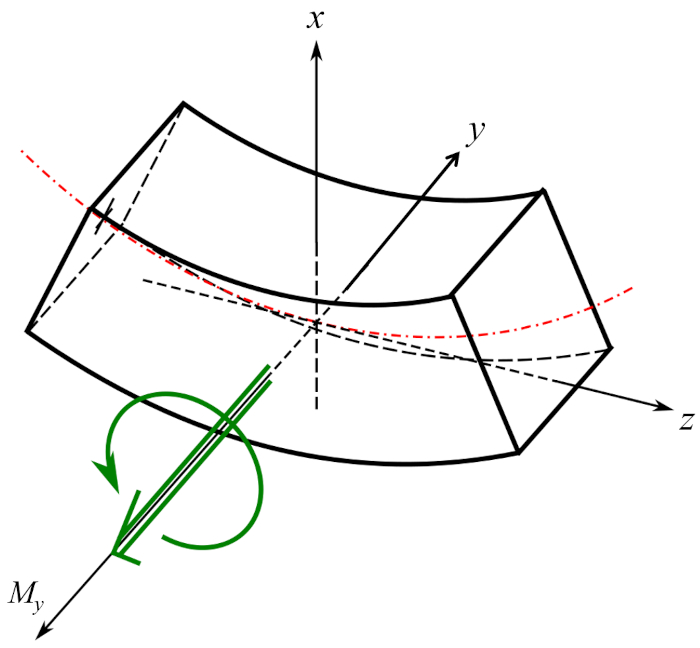
(ID 15884)
En general, el torque sobre la viga ($M_y$) debe aplicarse en ambos extremos para generar la flexi n:
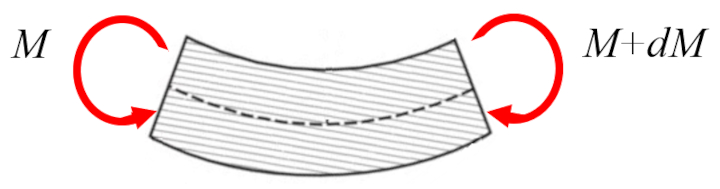
La diferencia entre ambos torques es igual al torque generado por la fuerza vertical al eje de la viga ($Q_z$), con un intervalo correspondiente a la variaci n de la posición a lo largo de la viga ($x$):
| $\displaystyle\frac{d M_y }{d x } = Q_z $ |
A su vez, la fuerza axial en la viga ($N_x$) puede variar a lo largo del eje:
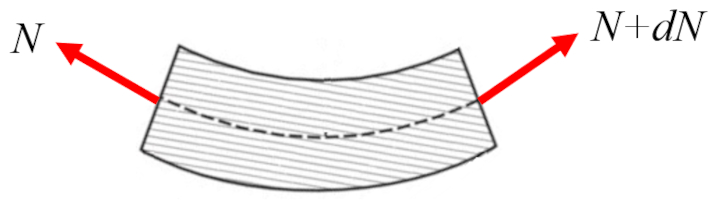
Esta variaci n corresponde a la fuerza axial lor largo en la viga ($n$) a lo largo del eje:
| $\displaystyle\frac{d N_x }{d x } = - n $ |
Finalmente, existe la fuerza vertical al eje de la viga ($Q_z$), que var a en funci n de la carga por largo sobre la viga ($q_z$), lo que puede corresponder al propio peso de la viga:
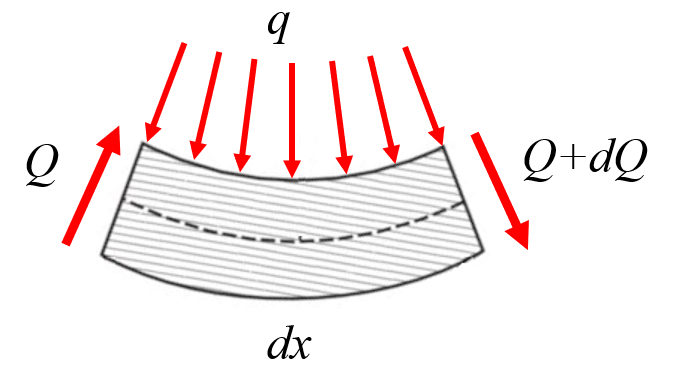
De esta manera, la variaci n de la fuerza vertical al eje de la viga ($Q_z$) a lo largo de la posición a lo largo de la viga ($x$) corresponde a la carga por largo sobre la viga ($q_z$) seg n:
| $\displaystyle\frac{d Q_z }{dx} = - q_z $ |
Al combinar la primera y ltima ecuaci n, se obtiene la ecuaci n de deformaci n:
| $\displaystyle\frac{d^2 M_y }{d x ^2} = - q $ |
(ID 15885)
Las fuerzas externas pueden actuar en un punto, generando torque en un punto, no catuando o como fuerza pareja como en el caso del peso de esta:
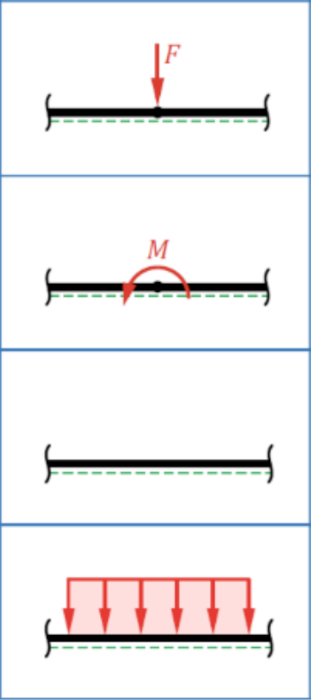
En todos los casos la fuerza y/o torque afecta directamente las ecuaciones de deformaci n y son parte integral de la soluci n de esta.
(ID 15886)
Una vez se tiene la soluci n deben satisfacrese las condciones de borde o sea que situaciones existen y que fuerzas o torque esto genera. Por ejemplo existe la situaci n:
* existe un punto de giro en el borde por lo que no se puede traspasar torque pero si fuerza axial y vertical.
* existe un punto de giro y la capacidad de desplazarse axialmente por lo que solo se puede traspasar una fuerza vertical
* la barra esta incerta en su base con lo que no se puede rotar por lo que soporta el torque necesario para ello
* si no se puede rotar pero si desplazar verticalmente se tiene que se le puede traspasar tanto torque como fuerza axial
* si no se puede rotar pero si mover axialmente
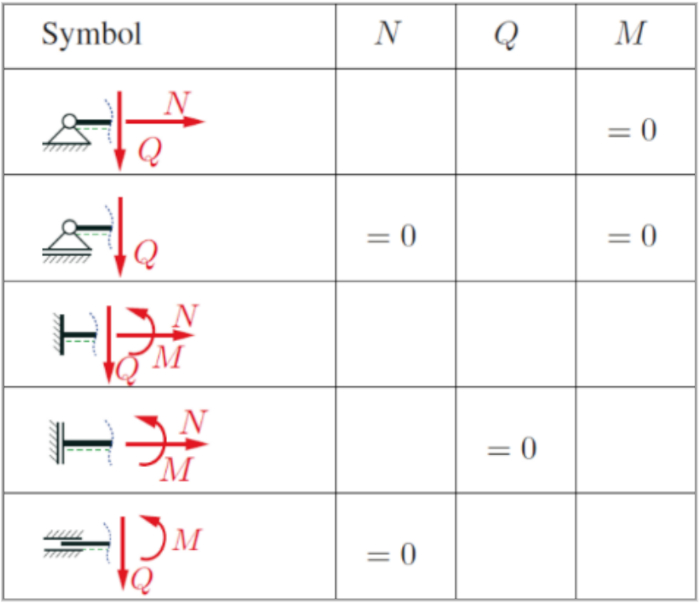
(ID 15887)
(ID 15571)
ID:(2062, 0)