Utilisateur:
Flexion élastique
Storyboard 
Lorsqu'un couple est appliqué à un corps, il peut être plié ou fléchi. La manière dont cela se produit dépend à la fois de la géométrie du corps et de la manière dont le couple est appliqué. De plus, il est possible d'estimer l'énergie élastique absorbée par le corps en fonction de la déformation qu'il subit.
ID:(2062, 0)
Flexion élastique
Description
Lorsqu'un couple est appliqué à un corps, il peut être plié ou fléchi. La manière dont cela se produit dépend à la fois de la géométrie du corps et de la manière dont le couple est appliqué. De plus, il est possible d'estimer l'énergie élastique absorbée par le corps en fonction de la déformation qu'il subit.
Variables
Calculs
à 
,
puis, sélectionnez la variable: 
à 
Calculs
Variable
Donnée
Calculer
Cible :
Équation
À utiliser
Équations
Si l'on observe comment a force verticale sur l'axe de la poutre ($Q_z$) varie en fonction de a charge par longueur sur la poutre ($q_z$) sur un l ment de a positionnement le long de la poutre ($x$), on obtient :
$Q - qdx - (Q + dQ) = 0$
donc :
$-qdx - dQ = 0$
ce qui conduit :
| $\displaystyle\frac{d Q_z }{dx} = - q_z $ |
(ID 15888)
La variation de le couple sur poutre ($M_y$) le long de a positionnement le long de la poutre ($x$) est de l'ordre du bras de levier de la longueur de l' l ment a positionnement le long de la poutre ($x$) multipli par a force verticale sur l'axe de la poutre ($Q_z$), par cons quent :
$-M - Qdx + (M + dM) = 0$
ce qui implique :
$-Qdx + dM = 0$
autrement dit :
| $\displaystyle\frac{d M_y }{d x } = Q_z $ |
(ID 15889)
Comme la d riv e de le couple sur poutre ($M_y$) par rapport a positionnement le long de la poutre ($x$) donne a force verticale sur l'axe de la poutre ($Q_z$) :
| $\displaystyle\frac{d M_y }{d x } = Q_z $ |
et que la d riv e de a force verticale sur l'axe de la poutre ($Q_z$) est gale moins a charge par longueur sur la poutre ($q_z$) :
| $\displaystyle\frac{d Q_z }{dx} = - q_z $ |
la d riv e de la premi re nous m ne :
| $\displaystyle\frac{d^2 M_y }{d x ^2} = - q $ |
(ID 15890)
Si l'on observe comment a force axiale dans la poutre ($N_x$) varie en fonction de a force axiale longue dans la poutre ($n$) sur un l ment de a positionnement le long de la poutre ($x$), on obtient :
$N - ndx - (N + dN) = 0$
donc :
$-ndx - dN = 0$
ce qui nous conduit :
| $\displaystyle\frac{d N_x }{d x } = - n $ |
(ID 15891)
Avec le couple sur poutre ($M_y$), a charge par longueur sur la poutre ($q_z$) et a positionnement le long de la poutre ($x$), l' quation du couple est tablie :
| $\displaystyle\frac{d^2 M_y }{d x ^2} = - q $ |
qui, combin e avec l' quation du d placement impliquant le module d'élasticité ($E$), le moment d'inertie de la section ($I_b$) et le déplacement z ($u_z$) :
| $ M_y = - E I_b \displaystyle\frac{d^2 u_z }{d x ^2}$ |
nous conduit :
| $ E I_b \displaystyle\frac{d^4 u_z }{d x ^4} = q_z $ |
(ID 15892)
Exemples
(ID 15570)
(ID 15884)
En g n ral, le couple sur poutre ($M_y$) doit tre appliqu aux deux extr mit s pour provoquer la flexion :
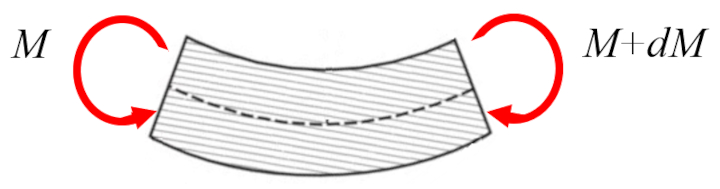
La diff rence entre les deux moments est gale au moment g n r par a force verticale sur l'axe de la poutre ($Q_z$), avec un intervalle correspondant la variation de a positionnement le long de la poutre ($x$) :
| $\displaystyle\frac{d M_y }{d x } = Q_z $ |
son tour, a force axiale dans la poutre ($N_x$) peut varier le long de l'axe :
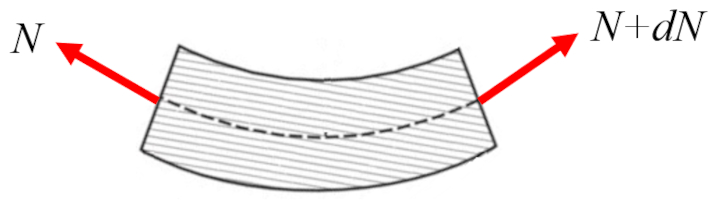
Cette variation correspond a force axiale longue dans la poutre ($n$) le long de l'axe :
| $\displaystyle\frac{d N_x }{d x } = - n $ |
Enfin, a force verticale sur l'axe de la poutre ($Q_z$) varie en fonction de a charge par longueur sur la poutre ($q_z$), ce qui peut correspondre au poids propre de la poutre :
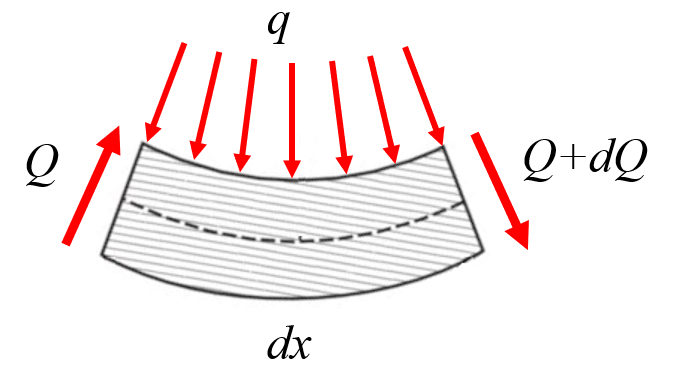
Ainsi, la variation de a force verticale sur l'axe de la poutre ($Q_z$) le long de a positionnement le long de la poutre ($x$) correspond a charge par longueur sur la poutre ($q_z$) comme suit :
| $\displaystyle\frac{d Q_z }{dx} = - q_z $ |
En combinant la premi re et la derni re quation, on obtient l quation de d formation :
| $\displaystyle\frac{d^2 M_y }{d x ^2} = - q $ |
(ID 15885)
(ID 15886)
(ID 15887)
(ID 15571)
A charge par longueur sur la poutre ($q_z$) peut tre calcul en fonction de la variation de a force verticale sur l'axe de la poutre ($Q_z$) le long de a positionnement le long de la poutre ($x$), par cons quent :
| $\displaystyle\frac{d Q_z }{dx} = - q_z $ |
(ID 15888)
A force axiale longue dans la poutre ($n$) peut tre calcul en fonction de la variation de a force axiale dans la poutre ($N_x$) le long de a positionnement le long de la poutre ($x$), par cons quent :
| $\displaystyle\frac{d N_x }{d x } = - n $ |
(ID 15891)
A force verticale sur l'axe de la poutre ($Q_z$) peut tre calcul en fonction de la mani re dont le couple sur poutre ($M_y$) varie le long de a positionnement le long de la poutre ($x$), par cons quent :
| $\displaystyle\frac{d M_y }{d x } = Q_z $ |
(ID 15889)
La courbure de le couple sur poutre ($M_y$) sur a positionnement le long de la poutre ($x$) est gale moins a charge par longueur sur la poutre ($q_z$) :
| $\displaystyle\frac{d^2 M_y }{d x ^2} = - q $ |
(ID 15890)
Le moment d'inertie de la section ($I_b$) dune section dune barre est calcul en int grant sur la section dans le plan a position en largeur sur la poutre ($y$) et a position en hauteur sur la poutre ($z$) :
| $ I_b =\displaystyle\int dz dy z^2 $ |
(ID 15881)
(ID 14195)
Avec l quation de le couple sur poutre ($M_y$) en fonction de a charge par longueur sur la poutre ($q_z$) et a positionnement le long de la poutre ($x$), et l quation pour la flexion impliquant le module d'élasticité ($E$), le moment d'inertie de la section ($I_b$) et le déplacement z ($u_z$), on obtient :
| $ E I_b \displaystyle\frac{d^4 u_z }{d x ^4} = q_z $ |
(ID 15892)
ID:(2062, 0)