Usuario:
Propagación de sonido
Storyboard 
La onda sonora se va propagando con lo que su energía por elemento de área se va reduciendo a medida que se aleja de la fuente.
ID:(386, 0)
Propagación de sonido
Descripción
La onda sonora se va propagando con lo que su energía por elemento de área se va reduciendo a medida que se aleja de la fuente.
Variables
Cálculos
a 
,
luego, seleccione la variable: 
a 
Cálculos
Variable
Dado
Calcule
Objetivo :
Ecuación
A utilizar
Ecuaciones
Ejemplos
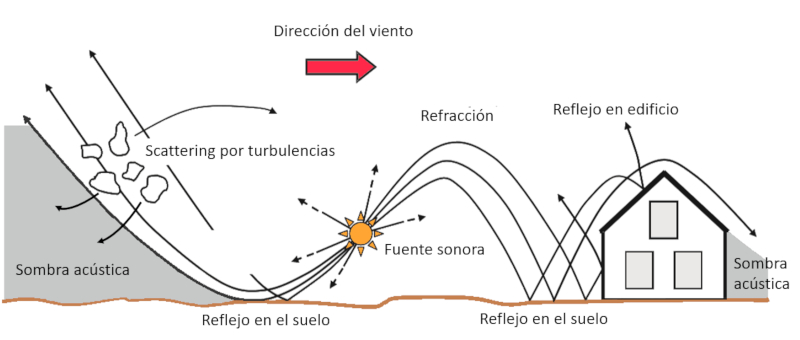
El sonido se propaga e interactua con los distintos bordes y objetos. En superficies planas se refleja bajo el mismo angulo que incide (suelo, edificio). Sin embargo el viento lleva a refracci n con lo que los haces se curvan:
(ID 516)
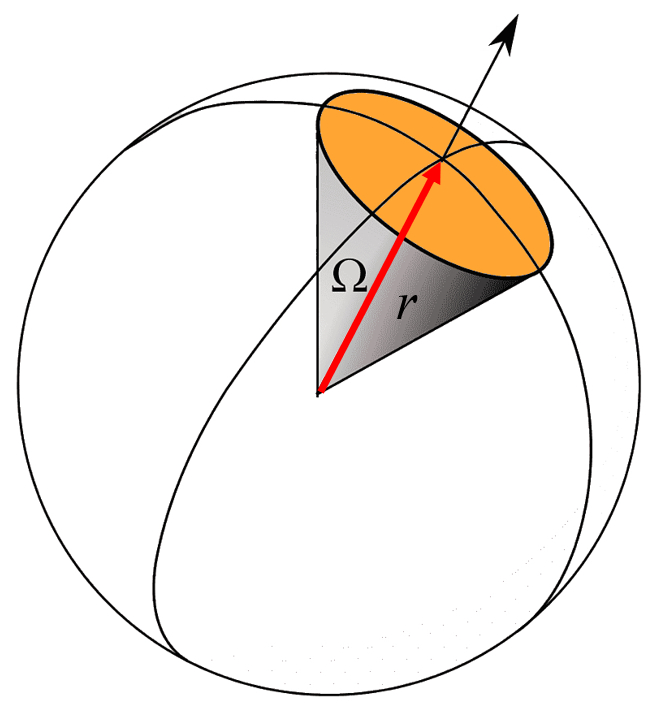
Para una fuente puntual, el sonido se propaga en todas las direcciones en forma uniforme. Por ello el nivel de sonido se va a ir reduciendo por el efecto que la energ a se reparte sobre una superficie de una esfera del radio
(ID 11829)
Si consideramos una fuente puntual, la intensidad del sonido es con
| $ I =\displaystyle\frac{ P }{ S }$ |
se propagara en forma esf rica. En este caso la superficie es con
| $ S = 4 \pi r ^2$ |
con lo que la intensidad es con
| $ I =\displaystyle\frac{1}{4 \pi }\displaystyle\frac{ P }{ r ^2}$ |
(ID 15566)
Si se considera una esfera en torno de la fuente a un radio
$W=4\pi r_0^2 I_0$
por lo que la intensidad es con distancia entre Emisor y Receptor $m$, intensidad en la distancia $W/m^2$ y potencia Sonora $W$
| $ I =\displaystyle\frac{1}{4 \pi }\displaystyle\frac{ P }{ r ^2}$ |
a una distancia
| $ I =\displaystyle\frac{ r_0 ^2}{ r ^2} I_0 $ |
(ID 15567)
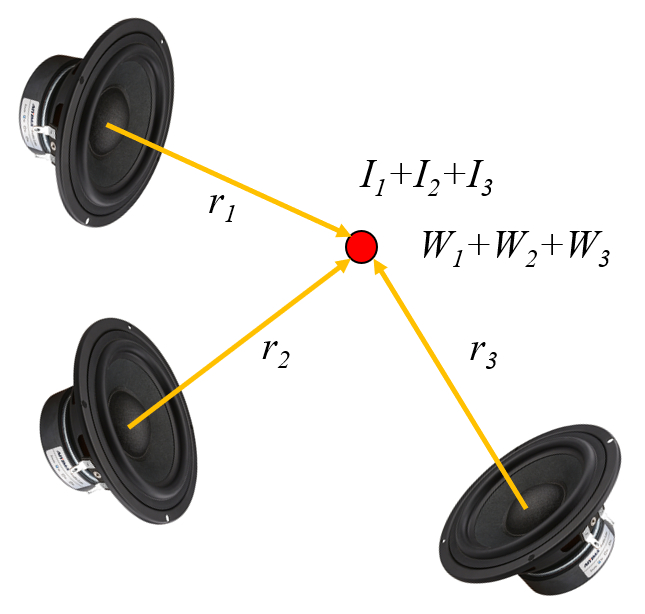
Como los distintos haces no interactuan la intensidad y la potencia que se da en cualquier punto del espacio es igual a la suma de las contribuciones individuales:
(ID 11830)
(ID 15455)
ID:(386, 0)