Druyd:Knowledge

Sound propagation

Storyboard

The sound wave is propagated so that its energy per area element is reduced as it moves away from the source.

>Model

ID:(386, 0)

Propagation of Sound

Note

ID:(516, 0)

Spherical propagation

Quote

ID:(11829, 0)

Sum of intensities and powers

Exercise

ID:(11830, 0)

Sound propagation

Description

The sound wave is propagated so that its energy per area element is reduced as it moves away from the source.

Variables

Symbol

Text

Variable

Value

Units

Calculate

MKS Value

MKS Units

$r$

Distance between Emitter and Receiver

$I_i$

I_i

Intensidad Sonora de la fuente i

W/m^2

$I$

Intensity in the distance

W/m^2

$I_0$

I_0

Intensity on the Surface of the Source

W/m^2

$\rho$

rho

Mean density

kg/m^3

$L$

Noise level

$I_{ref}$

I_ref

Reference intensity

W/m^2

$p_{ref}$

p_ref

Reference pressure

$I$

Sound Intensity

W/m^2

$P$

Sound Power

$p_s$

p_s

Sound pressure

$r_0$

r_0

Source Size

$c$

Speed of sound

m/s

$I_{tot}$

I_tot

Total Loudness

W/m^2

Calculations

Equation

Number

First, select the equation:

, then, select the variable:

Symbol

Equation

Solved

Translated

Calculations

Symbol

Equation

Solved

Translated

Variable

Given

Calculate

Target :

Equation

To be used

Equations

$ L = 10 log_{10}\left(\displaystyle\frac{ I }{ I_{ref} }\right)$

L = 10* log10( I / I_ref )

(ID 3194)

$ I =\displaystyle\frac{1}{4 \pi }\displaystyle\frac{ P }{ r ^2}$

I = P /(4 pi r ^2)

(ID 3402)

$ I =\displaystyle\frac{ r_0 ^2}{ r ^2} I_0 $

I =( r_0 ^2/ r ^2) I_0

(ID 3403)

$ L = 20 \log_{10}\left(\displaystyle\frac{ p_s }{ p_{ref} }\right)$

L = 20* log10( p_s / p_ref )

(ID 3407)

$ I_{ref} =\displaystyle\frac{ p_{ref} ^2}{2 \rho c }$

I_ref = p_ref ^2/(2* rho * c )

(ID 3409)

$ I = \displaystyle\sum_i I_i $

I = sum( I_i , i )

(ID 11831)

Examples

Propagation of Sound

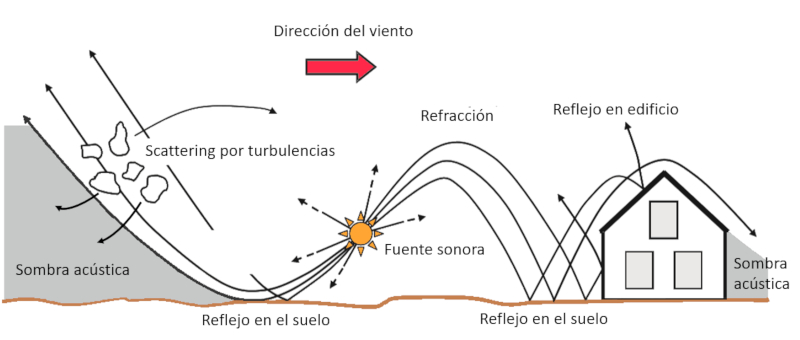
Sound propagates and interacts with various edges and objects. On flat surfaces it is reflected under the same angle it affects (ground, building). However, the wind leads to refraction with what the beams bend:

(ID 516)

Spherical propagation

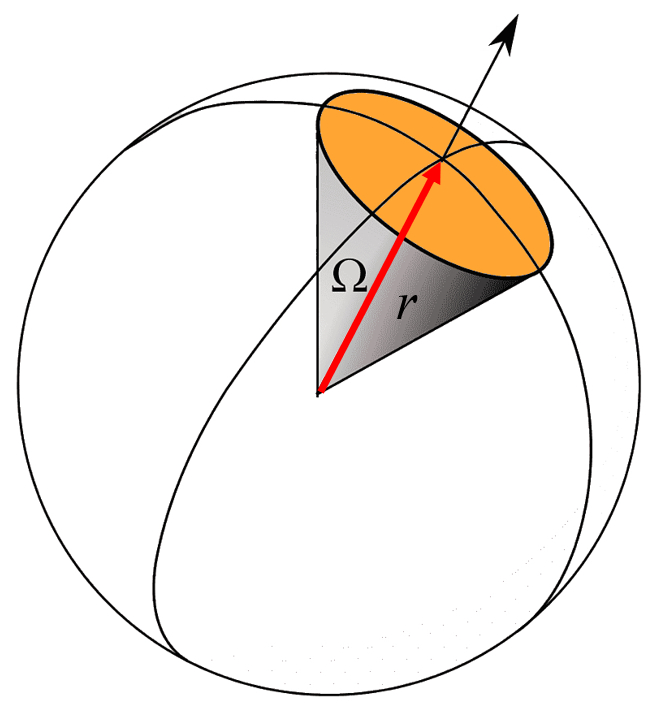
For a point source, the sound spreads in all directions uniformly. Therefore, the sound level will be reduced due to the effect that the energy is distributed over a surface of a sphere of radius r equal to the path traveled

(ID 11829)

Propagation of the intensity

Si consideramos una fuente puntual, la intensidad del sonido es con

$ I =\displaystyle\frac{ P }{ S }$

se propagara en forma esf rica. En este caso la superficie es con

$ S = 4 \pi r ^2$

con lo que la intensidad es con

$ I =\displaystyle\frac{1}{4 \pi }\displaystyle\frac{ P }{ r ^2}$

(ID 15566)

Propagation depending on the Intensity at source

Si se considera una esfera en torno de la fuente a un radio r_0 la potencia W sera igual a

$W=4\pi r_0^2 I_0$

por lo que la intensidad es con distance between Emitter and Receiver $m$, intensity in the distance $W/m^2$ and sound Power $W$

$ I =\displaystyle\frac{1}{4 \pi }\displaystyle\frac{ P }{ r ^2}$

a una distancia r tendr con distance between Emitter and Receiver $m$, intensity in the distance $W/m^2$ and sound Power $W$ la magnitud:

$ I =\displaystyle\frac{ r_0 ^2}{ r ^2} I_0 $

(ID 15567)

Sum of intensities and powers

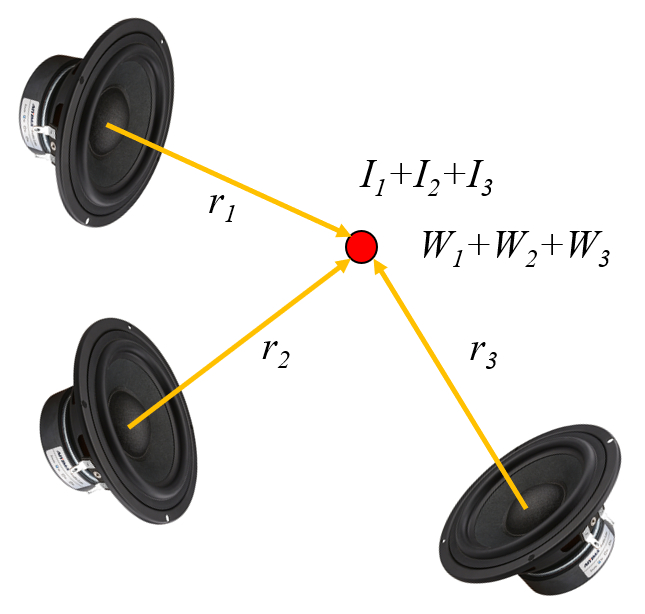
Since the different beams do not interact, the intensity and power that occurs at any point in space is equal to the sum of the individual contributions:

(ID 11830)

Model

(ID 15455)

ID:(386, 0)