Propagación de sonido
Storyboard 
La onda sonora se va propagando con lo que su energía por elemento de área se va reduciendo a medida que se aleja de la fuente.
ID:(386, 0)
Propagación de la intensidad
Definición 
Si consideramos una fuente puntual, la intensidad del sonido es con
| $ I =\displaystyle\frac{ P }{ S }$ |
se propagara en forma esférica. En este caso la superficie es con
| $ S = 4 \pi r ^2$ |
con lo que la intensidad es con
| $ I =\displaystyle\frac{1}{4 \pi }\displaystyle\frac{ P }{ r ^2}$ |
ID:(15566, 0)
Propagación en función de la intensidad en el origen
Imagen 
Si se considera una esfera en torno de la fuente a un radio
$W=4\pi r_0^2 I_0$
por lo que la intensidad es con
| $ I =\displaystyle\frac{1}{4 \pi }\displaystyle\frac{ P }{ r ^2}$ |
a una distancia
| $ I =\displaystyle\frac{ r_0 ^2}{ r ^2} I_0 $ |
ID:(15567, 0)
Propagación de sonido
Nota 
El sonido se propaga e interactua con los distintos bordes y objetos. En superficies planas se refleja bajo el mismo angulo que incide (suelo, edificio). Sin embargo el viento lleva a refracción con lo que los haces se curvan:
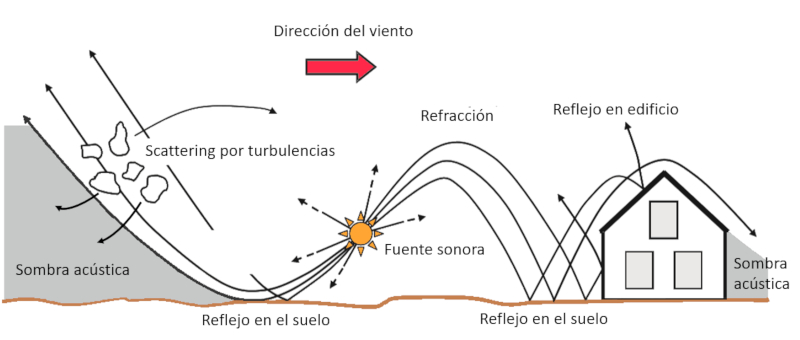
ID:(516, 0)
Propagación esférica
Cita 
Para una fuente puntual, el sonido se propaga en todas las direcciones en forma uniforme. Por ello el nivel de sonido se va a ir reduciendo por el efecto que la energía se reparte sobre una superficie de una esfera del radio
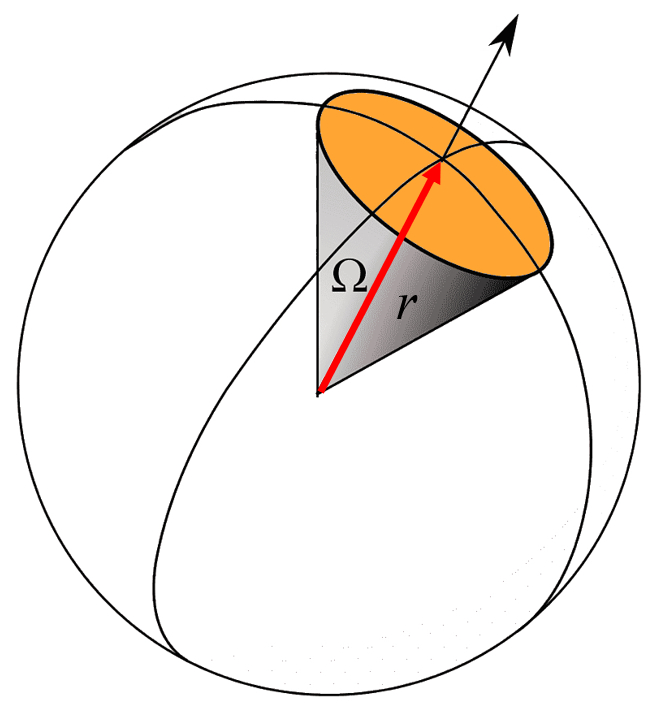
ID:(11829, 0)
Suma de intensidades y potencias
Ejercicio 
Como los distintos haces no interactuan la intensidad y la potencia que se da en cualquier punto del espacio es igual a la suma de las contribuciones individuales:
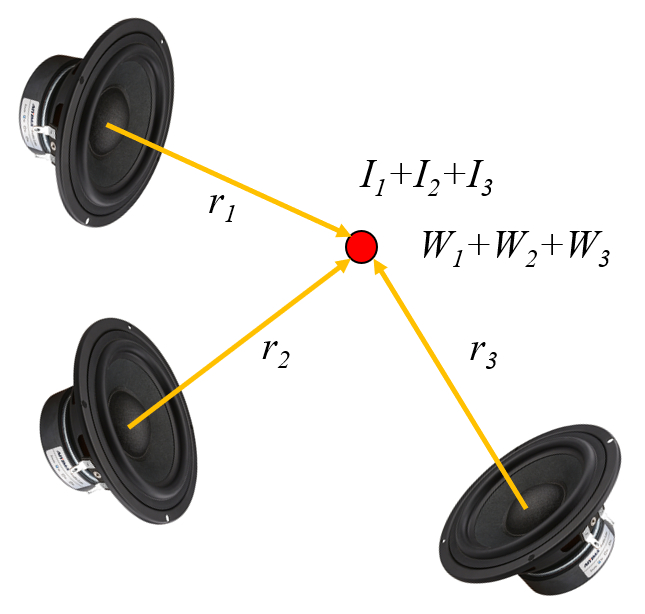
ID:(11830, 0)
Propagación de sonido
Storyboard 
La onda sonora se va propagando con lo que su energía por elemento de área se va reduciendo a medida que se aleja de la fuente.
Variables
Cálculos
Cálculos
Ecuaciones
Ejemplos
El sonido se propaga e interactua con los distintos bordes y objetos. En superficies planas se refleja bajo el mismo angulo que incide (suelo, edificio). Sin embargo el viento lleva a refracci n con lo que los haces se curvan:
Para una fuente puntual, el sonido se propaga en todas las direcciones en forma uniforme. Por ello el nivel de sonido se va a ir reduciendo por el efecto que la energ a se reparte sobre una superficie de una esfera del radio
Si consideramos una fuente puntual, la intensidad del sonido es con
se propagara en forma esf rica. En este caso la superficie es con
con lo que la intensidad es con
Si se considera una esfera en torno de la fuente a un radio
$W=4\pi r_0^2 I_0$
por lo que la intensidad es con
a una distancia
Como los distintos haces no interactuan la intensidad y la potencia que se da en cualquier punto del espacio es igual a la suma de las contribuciones individuales:
Como los distintos haces no interactuan la intensidad que se da en cualquier punto del espacio es igual a la suma de las contribuciones individuales.
Con
Si se considera una esfera en torno de la fuente a un radio
Al igual que en otros sistemas de percepci n del ser humano, nuestro o do es capaz de captar variaciones de presi n en un rango muy amplio $(10^{-5}-10^2 Pa)$. Sin embargo, cuando percibimos una duplicaci n en la se al, esto no corresponde al doble de presi n o intensidad sonora, sino a la cuadratura de estas magnitudes. En otras palabras, nuestra capacidad de captar se ales trabaja con una escala logar tmica y no lineal.
Por ello, se indica el nivel de ruido ($L$) no en la intensidad Sonora ($I$) o la intensidad de referencia ($I_{ref}$), sino en el logaritmo base diez de dichas magnitudes. En particular, se toma la menor intensidad sonora que podemos percibir, la intensidad de referencia ($I_{ref}$)
, y se usa esta como referencia. La nueva escala se define con
La presi n sonora que podemos detectar con nuestro o do, designada como la presión de referencia, agua ($p_{ref}$), es de $2 \times 10^{-5} , Pa$.
Dado que la intensidad Sonora ($I$) est relacionado con la presión sonora ($p_s$), la densidad del medio ($\rho$) y la velocidad del sonido ($c$), y es igual a
podemos calcular un valor de la intensidad de referencia ($I_{ref}$) basado en el valor de la presión de referencia, agua ($p_{ref}$):
Esto se logra con una densidad de $1.27 , kg/m^3$ y una velocidad del sonido de $331 , m/s$, equivalente a $9.5 \times 10^{-13} , W/m^2$.
El nivel de ruido ($L$) abarca un amplio rango de la presión sonora ($p_s$), lo que hace til definir una escala que mitigue esta dificultad. Para ello, podemos trabajar con el logaritmo de la presi n normalizado por un valor que corresponda al cero en esta escala. Si tomamos la presi n m nima que una persona puede detectar y que definimos como la presión de referencia ($p_{ref}$), podemos definir una escala mediante:
que comienza en 0 para el rango audible. En el caso del aire, la presión de referencia ($p_{ref}$) es de $20 \mu Pa$.
ID:(386, 0)
