Schall Ausbreitung
Storyboard 
Die Schallwelle breitet sich so aus, dass ihre Energie pro Flächenelement verringert wird, wenn sie sich von der Quelle entfernt.
ID:(386, 0)
Ausbreitung abhängig von der Intensität an der Quelle
Definition 
Si se considera una esfera en torno de la fuente a un radio
$W=4\pi r_0^2 I_0$
por lo que la intensidad es con
| $ I =\displaystyle\frac{1}{4 \pi }\displaystyle\frac{ P }{ r ^2}$ |
a una distancia
| $ I =\displaystyle\frac{ r_0 ^2}{ r ^2} I_0 $ |
ID:(15567, 0)
Ausbreitung der Intensität
Bild 
Si consideramos una fuente puntual, la intensidad del sonido es con
| $ I =\displaystyle\frac{ P }{ S }$ |
se propagara en forma esférica. En este caso la superficie es con
| $ S = 4 \pi r ^2$ |
con lo que la intensidad es con
| $ I =\displaystyle\frac{1}{4 \pi }\displaystyle\frac{ P }{ r ^2}$ |
ID:(15566, 0)
Schallausbreitung
Notiz 
Schall breitet sich aus und interagiert mit verschiedenen Kanten und Objekten. Auf ebenen Flächen wird es unter dem gleichen Winkel reflektiert, den es beeinflusst (Boden, Gebäude). Der Wind führt jedoch zu einer Brechung mit dem, was die Strahlen biegen:
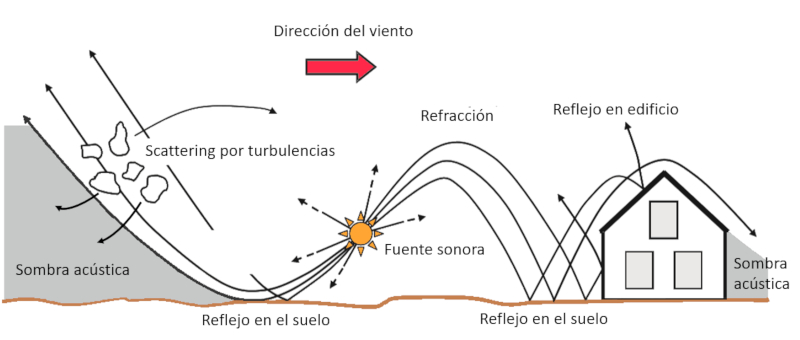
ID:(516, 0)
Sphärische Ausbreitung
Zitat 
Bei einer Punktquelle breitet sich der Schall gleichmäßig in alle Richtungen aus. Daher wird der Schallpegel aufgrund des Effekts verringert, dass die Energie über eine Oberfläche einer Kugel mit dem Radius
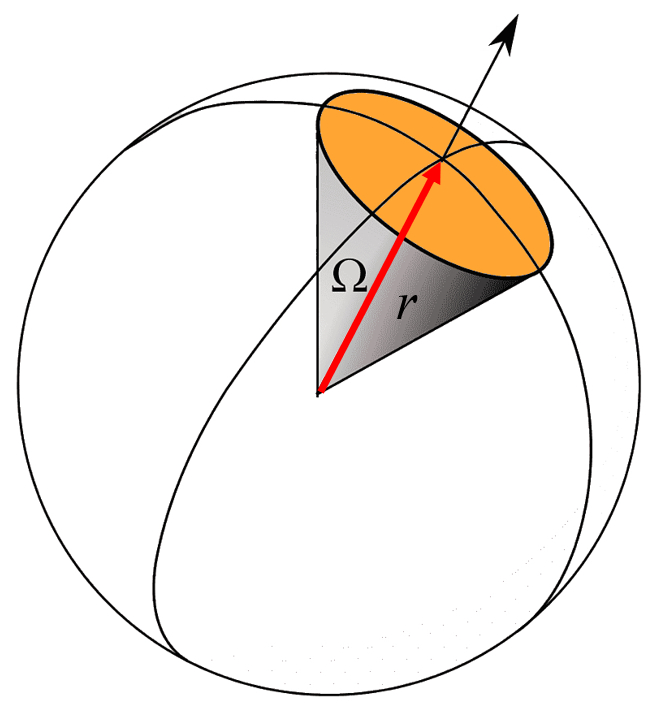
ID:(11829, 0)
Summe der Intensitäten und Kräfte
Übung 
Da die verschiedenen Strahlen nicht interagieren, entspricht die Intensität und Leistung, die an einem beliebigen Punkt im Raum auftritt, der Summe der einzelnen Beiträge:
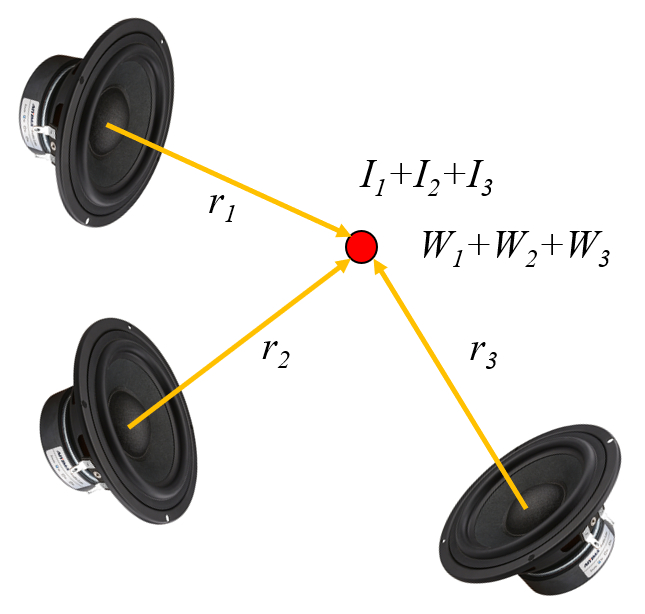
ID:(11830, 0)
Schall Ausbreitung
Storyboard 
Die Schallwelle breitet sich so aus, dass ihre Energie pro Flächenelement verringert wird, wenn sie sich von der Quelle entfernt.
Variablen
Berechnungen
Berechnungen
Gleichungen
Beispiele
Schall breitet sich aus und interagiert mit verschiedenen Kanten und Objekten. Auf ebenen Fl chen wird es unter dem gleichen Winkel reflektiert, den es beeinflusst (Boden, Geb ude). Der Wind f hrt jedoch zu einer Brechung mit dem, was die Strahlen biegen:
Bei einer Punktquelle breitet sich der Schall gleichm ig in alle Richtungen aus. Daher wird der Schallpegel aufgrund des Effekts verringert, dass die Energie ber eine Oberfl che einer Kugel mit dem Radius
Si consideramos una fuente puntual, la intensidad del sonido es con
se propagara en forma esf rica. En este caso la superficie es con
con lo que la intensidad es con
Si se considera una esfera en torno de la fuente a un radio
$W=4\pi r_0^2 I_0$
por lo que la intensidad es con
a una distancia
Da die verschiedenen Strahlen nicht interagieren, entspricht die Intensit t und Leistung, die an einem beliebigen Punkt im Raum auftritt, der Summe der einzelnen Beitr ge:
Como los distintos haces no interactuan la intensidad que se da en cualquier punto del espacio es igual a la suma de las contribuciones individuales.
Con
Si consideramos una fuente puntual, la intensidad del sonido es con
se propagara en forma esf rica. En este caso la superficie es con
con lo que la intensidad es con
Si se considera una esfera en torno de la fuente a un radio
$W=4\pi r_0^2 I_0$
por lo que la intensidad es con
a una distancia
Wie in anderen menschlichen Wahrnehmungssystemen ist unser Geh r in der Lage, Druckschwankungen in einem weiten Bereich wahrzunehmen $(10^{-5}-10^2 Pa)$. Wenn wir jedoch ein Signal verdoppeln, entspricht dies nicht dem doppelten Druck oder Schallintensit t, sondern vielmehr dem Quadrat dieser Gr en. Mit anderen Worten: Unsere F higkeit, Signale wahrzunehmen, arbeitet auf einer logarithmischen und nichtlinearen Skala.
Daher wird der Geräuschpegel ($L$) nicht in die Schallintensität ($I$) oder die Referenz Intensity ($I_{ref}$) angegeben, sondern im Zehnerlogarithmus dieser Gr en. Insbesondere nehmen wir die niedrigste Schallintensit t wahr, die wir wahrnehmen k nnen, die Referenz Intensity ($I_{ref}$)
, und verwenden sie als Referenz. Die neue Skala wird mit
Der Schalldruck, den wir mit unserem Ohr wahrnehmen k nnen und der mit die Referenzdruck, Wasser ($p_{ref}$) bezeichnet wird, betr gt $2 \times 10^{-5} , Pa$.
Da die Schallintensität ($I$) mit die Schalldruck ($p_s$), die Mittlere Dichte ($\rho$) und die Speed of Sound ($c$) gleich ist
kann ein Wert von die Referenz Intensity ($I_{ref}$) basierend auf dem Wert von die Referenzdruck, Wasser ($p_{ref}$) berechnet werden:
Dies wird mit einer Dichte von $1.27 , kg/m^3$ und einer Schallgeschwindigkeit von $331 , m/s$ erreicht, was $9.5 \times 10^{-13} , W/m^2$ entspricht.
Der Geräuschpegel ($L$) umfasst einen weiten Bereich von die Schalldruck ($p_s$), was es sinnvoll macht, eine Skala zu definieren, die diese Schwierigkeit mildert. Daf r k nnen wir mit dem Logarithmus des Drucks arbeiten, der durch einen Wert normalisiert ist, der null auf dieser Skala entspricht. Wenn wir den minimalen Druck nehmen, den eine Person wahrnehmen kann, definiert als die Referenzdruck ($p_{ref}$), k nnen wir eine Skala definieren mittels:
die im h rbaren Bereich bei 0 beginnt. Im Fall von Luft betr gt die Referenzdruck ($p_{ref}$) $20 \mu Pa$.
ID:(386, 0)
