Posição, mais dimensões
Storyboard 
Para descrever a posição de um objeto em mais de uma dimensão, é necessário introduzir um sistema de coordenadas multidimensional. Esse sistema é caracterizado por associar a cada ponto no espaço um conjunto único de parâmetros. O número desses parâmetros é igual ao número de dimensões.
A escolha do sistema de coordenadas pode depender do problema que está sendo modelado. Por um lado, busca-se ter o menor número possível de dimensões e, por outro lado, garantir que, na medida do possível, a descrição do movimento em cada dimensão seja independente das outras dimensões. Isso facilita a solução, pois cada dimensão pode ser estudada separadamente.
ID:(1201, 0)
Dimensões
Definição 
Dimensões são os parâmetros necessários para descrever a posição de um sistema em um espaço particular. Estes parâmetros podem incluir distância, comprimento, latitude e altura, entre outros. Isso permite que um sistema seja localizado em um espaço particular. Por exemplo, um veículo em uma estrada precisa apenas de um parâmetro para indicar sua localização, enquanto um barco no oceano precisa de dois parâmetros e um avião, três.
ID:(479, 0)
Representação da posição em duas dimensões
Imagem 
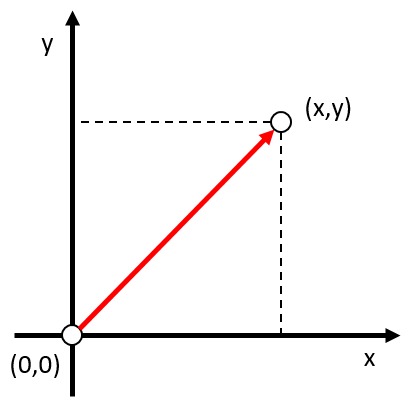
Em um sistema de duas dimensões, a posição de um objeto pode ser representada por um vetor, o qual indica a distância da origem de zero (coordenadas $(0,0)$) na direção em que o objeto se encontra. Ambos os coordenados são medidos como uma quantidade positiva ou negativa, dependendo se o objeto está na direção positiva ou negativa do eixo respectivo. Esta posição pode ser representada, por exemplo, pelo parâmetro $(x,y)$, onde os escalares $x$ e $y$ indicam a distância da origem do objeto em cada eixo.
ID:(2234, 0)
Representação da posição em três dimensões
Nota 
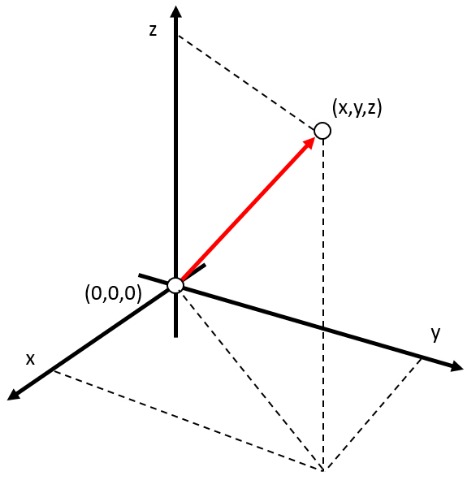
Em um sistema de duas dimensões, a posição de um objeto pode ser representada por um vetor, o qual indica a distância da origem de zero (coordenadas $(0,0,0)$) na direção em que o objeto se encontra. Ambos os coordenados são medidos como uma quantidade positiva ou negativa, dependendo se o objeto está na direção positiva ou negativa do eixo respectivo. Esta posição pode ser representada, por exemplo, pelo parâmetro $(x,y,z)$, onde os escalares $x$, $y$ e $z$ indicam a distância da origem do objeto em cada eixo.
ID:(2235, 0)
Odômetro
Citar 
Um odômetro é um dispositivo usado para medir a distância percorrida por um veículo. Normalmente está localizado no painel do carro e pode ser usado para acompanhar a distância total percorrida. Um odômetro funciona contando o número de rotações de um eixo de transmissão ligado às rodas do veículo. À medida que o veículo se move, o eixo de transmissão gira e cada rotação é contada e registrada no odômetro. O odômetro é geralmente calibrado para que possa medir com precisão as distâncias percorridas em milhas ou quilômetros.

ID:(480, 0)
Telêmetro a laser
Exercício 
Um medidor a laser é um dispositivo que usa um feixe de laser para medir a distância entre dois pontos. Ele funciona enviando um pulso de laser, que é refletido pelo objeto a ser medido e então detectado pelo medidor a laser. O tempo que leva o pulso de laser para viajar do medidor a laser para o objeto e de volta pode então ser usado para calcular a distância entre os dois pontos. Medidores a laser são comumente usados em levantamentos, navegação e outras aplicações onde medidas precisas são necessárias.

ID:(481, 0)
GPS (Sistema de Posicionamento Global)
Equação 
O Sistema de Posicionamento Global (GPS) é um sistema de navegação baseado em satélite que usa uma rede de 24 satélites orbitando a Terra para determinar a localização exata de uma pessoa ou objeto no planeta. Os receptores GPS calculam a distância para cada satélite medindo a quantidade de tempo que leva para as sinalizar viajarem do satélite para o receptor. Uma vez que essas distâncias são conhecidas, o receptor pode usar um processo chamado trilateração para calcular sua localização exata, incluindo longitude e latitude, bem como altitude. Isso pode ser usado para medir distâncias entre dois locais, bem como o comprimento de um caminho percorrido por uma pessoa ou objeto.

ID:(474, 0)
Distância percorrida
Script 
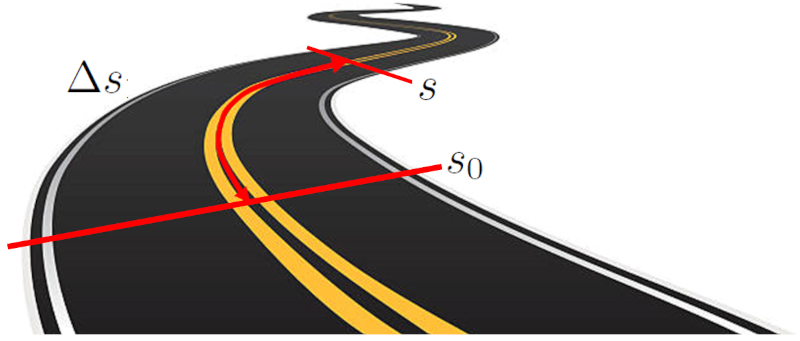
La distância percorrida em um tempo ($\Delta s$) por um objeto é medida medindo a distância entre dois pontos específicos ao longo de uma trajetória. Essa trajetória pode ser uma linha reta em um eixo cartesiano ou um caminho curvo. A distância é calculada medindo o comprimento da trajetória entre os dois pontos de partida e chegada.
ID:(9495, 0)
Posição inicial em mais dimensões
Variable 
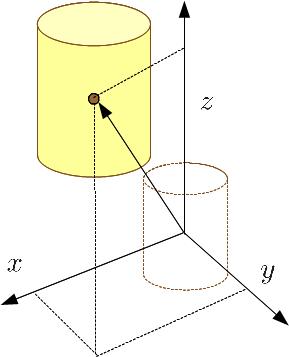
A posição inicial de um objeto é sua localização antes de qualquer movimento começar. Esta posição pode ser definida em mais de uma dimensão por um vetor, que vai do ponto de origem do sistema de coordenadas para o objeto, tendo o mesmo número de componentes que as dimensões existentes.
ID:(2236, 0)
Distância percorrida em mais dimensões
Audio 
Para descrever o movimento de um objeto, calculamos a diferença entre um ponto inicial e um ponto final. Essa diferença, chamada de distância, nem sempre corresponde à distância real percorrida pelo objeto se o caminho for curvo. A curvatura do caminho faz com que a distância percorrida seja maior do que a distância entre os dois pontos. Se os pontos estão próximos um do outro, a curvatura é desprezível e a distância percorrida coincide com a distância entre os dois pontos.
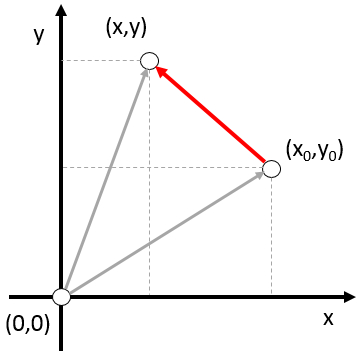
Nesse caso, falamos de uma distância infinitesimal.
ID:(9496, 0)
Posição, mais dimensões
Descrição 
Para descrever a posição de um objeto em mais de uma dimensão, é necessário introduzir um sistema de coordenadas multidimensional. Esse sistema é caracterizado por associar a cada ponto no espaço um conjunto único de parâmetros. O número desses parâmetros é igual ao número de dimensões. A escolha do sistema de coordenadas pode depender do problema que está sendo modelado. Por um lado, busca-se ter o menor número possível de dimensões e, por outro lado, garantir que, na medida do possível, a descrição do movimento em cada dimensão seja independente das outras dimensões. Isso facilita a solução, pois cada dimensão pode ser estudada separadamente.
Variáveis
Cálculos
Cálculos
Equações
Exemplos
Dimens es s o os par metros necess rios para descrever a posi o de um sistema em um espa o particular. Estes par metros podem incluir dist ncia, comprimento, latitude e altura, entre outros. Isso permite que um sistema seja localizado em um espa o particular. Por exemplo, um ve culo em uma estrada precisa apenas de um par metro para indicar sua localiza o, enquanto um barco no oceano precisa de dois par metros e um avi o, tr s.
(ID 479)
Em um sistema de duas dimens es, a posi o de um objeto pode ser representada por um vetor, o qual indica a dist ncia da origem de zero (coordenadas $(0,0)$) na dire o em que o objeto se encontra. Ambos os coordenados s o medidos como uma quantidade positiva ou negativa, dependendo se o objeto est na dire o positiva ou negativa do eixo respectivo. Esta posi o pode ser representada, por exemplo, pelo par metro $(x,y)$, onde os escalares $x$ e $y$ indicam a dist ncia da origem do objeto em cada eixo.

(ID 2234)
Em um sistema de duas dimens es, a posi o de um objeto pode ser representada por um vetor, o qual indica a dist ncia da origem de zero (coordenadas $(0,0,0)$) na dire o em que o objeto se encontra. Ambos os coordenados s o medidos como uma quantidade positiva ou negativa, dependendo se o objeto est na dire o positiva ou negativa do eixo respectivo. Esta posi o pode ser representada, por exemplo, pelo par metro $(x,y,z)$, onde os escalares $x$, $y$ e $z$ indicam a dist ncia da origem do objeto em cada eixo.

(ID 2235)
Um od metro um dispositivo usado para medir a dist ncia percorrida por um ve culo. Normalmente est localizado no painel do carro e pode ser usado para acompanhar a dist ncia total percorrida. Um od metro funciona contando o n mero de rota es de um eixo de transmiss o ligado s rodas do ve culo. medida que o ve culo se move, o eixo de transmiss o gira e cada rota o contada e registrada no od metro. O od metro geralmente calibrado para que possa medir com precis o as dist ncias percorridas em milhas ou quil metros.

(ID 480)
Um medidor a laser um dispositivo que usa um feixe de laser para medir a dist ncia entre dois pontos. Ele funciona enviando um pulso de laser, que refletido pelo objeto a ser medido e ent o detectado pelo medidor a laser. O tempo que leva o pulso de laser para viajar do medidor a laser para o objeto e de volta pode ent o ser usado para calcular a dist ncia entre os dois pontos. Medidores a laser s o comumente usados em levantamentos, navega o e outras aplica es onde medidas precisas s o necess rias.

(ID 481)
O Sistema de Posicionamento Global (GPS) um sistema de navega o baseado em sat lite que usa uma rede de 24 sat lites orbitando a Terra para determinar a localiza o exata de uma pessoa ou objeto no planeta. Os receptores GPS calculam a dist ncia para cada sat lite medindo a quantidade de tempo que leva para as sinalizar viajarem do sat lite para o receptor. Uma vez que essas dist ncias s o conhecidas, o receptor pode usar um processo chamado trilatera o para calcular sua localiza o exata, incluindo longitude e latitude, bem como altitude. Isso pode ser usado para medir dist ncias entre dois locais, bem como o comprimento de um caminho percorrido por uma pessoa ou objeto.

(ID 474)
La distância percorrida em um tempo ($\Delta s$) para um objeto determinado medindo a dist ncia entre dois pontos espec ficos ao longo de um trajeto. Esse trajeto pode ser uma linha reta em um eixo cartesiano ou um caminho curvo. A dist ncia calculada como o comprimento do trajeto que conecta os pontos inicial e final.

Dist ncia percorrida de um ponto inicial at um ponto final
Como o valor de la distância percorrida em um tempo ($\Delta s$) calculado como a diferen a entre la posição ($s$) e la velocidade ($s_0$):
| $ \Delta s = s_2 - s_1 $ |
poss vel "deslocar" a origem da posi o somando um valor constante $d$ a ambas as magnitudes:
$s \rightarrow s + d$
$s_0 \rightarrow s_0 + d$
sem afetar o resultado da dist ncia percorrida:
$\Delta s = s - s_0 \rightarrow (s + d) - (s_0 + d) = s - s_0 = \Delta s$
Esse conceito conhecido como invari ncia espacial, o que implica que o valor da dist ncia percorrida n o depende do ponto espec fico onde a medi o come a.
Isso significa que as leis formuladas com base nesse princ pio ser o invariantes espaciais, ou seja, continuar o v lidas independentemente do lugar onde a medi o realizada.
(ID 9495)
Para descrever o movimento de um objeto, necess rio calcular a dist ncia que ele percorreu. Para fazer isso, os pontos inicial e final do objeto s o definidos usando vetores, e a dist ncia calculada subtraindo um vetor do outro. Isso s coincide com o caminho percorrido se o deslocamento for retil neo, o que geralmente verdadeiro quando ambos os pontos est o muito pr ximos, como no caso de la distância percorrida ($\Delta\vec{s}$) subtraindo la posição de origem ($\vec{s}_0$) de la posição real ($\vec{s}$):
| $ \Delta\vec{s} \equiv \vec{s} - \vec{s}_0 $ |
(ID 714)
A posi o inicial de um objeto sua localiza o antes de qualquer movimento come ar. Esta posi o pode ser definida em mais de uma dimens o por um vetor, que vai do ponto de origem do sistema de coordenadas para o objeto, tendo o mesmo n mero de componentes que as dimens es existentes.

(ID 2236)
Para descrever o movimento de um objeto, calculamos a diferen a entre um ponto inicial e um ponto final. Essa diferen a, chamada de dist ncia, nem sempre corresponde dist ncia real percorrida pelo objeto se o caminho for curvo. A curvatura do caminho faz com que a dist ncia percorrida seja maior do que a dist ncia entre os dois pontos. Se os pontos est o pr ximos um do outro, a curvatura desprez vel e a dist ncia percorrida coincide com a dist ncia entre os dois pontos.

Nesse caso, falamos de uma dist ncia infinitesimal.
(ID 9496)
No caso de um espa o com mais de uma dimens o, o caminho entre dois pontos n o precisa ser necessariamente reto, como acontece em espa os unidimensionais. Nessas situa es, um vetor que representa a dist ncia entre dois pontos ao longo do caminho ser sempre igual ou menor do que a dist ncia real ao longo do caminho. No entanto, eles coincidir o se a dist ncia entre os dois pontos for infinitesimal ou muito pequena. Portanto, til definir o vetor infinitesimal, que nos permite descrever o comportamento de um objeto em um espa o cont nuo de forma precisa.
Portanto, o elemento do caminho percorrido ($d\vec{s}$) introduzido como a diferen a entre la posição real ($\vec{s}$) e la posição de origem ($\vec{s}_0$) como:
| $d\vec{s} \equiv \vec{s} - \vec{s}_0 $ |
(ID 9497)
ID:(1201, 0)
