Position, more dimensions
Storyboard 
To describe the position of an object in more than one dimension, it is necessary to introduce a multi-dimensional coordinate system. This system is characterized by associating a unique set of parameters with each point in space. The number of these parameters is equal to the number of dimensions.
The choice of coordinate system can depend on the problem being modeled. On one hand, the aim is to have the fewest possible number of dimensions, and on the other hand, to ensure that, as much as possible, the description of motion in each dimension is independent of the other dimensions. This facilitates the solution, as each dimension can be studied separately.
ID:(1201, 0)
Dimensions
Definition 
Dimensions are the parameters needed to describe the position of a system in a particular space. These parameters can include distance, length, latitude, and height, among others. This allows a system to be located in a particular space. For example, a vehicle on a road needs only one parameter to indicate its location, while a boat on the ocean needs two parameters and an airplane three.
ID:(479, 0)
Representation of the position in two dimensions
Image 
In a two-dimensional system, the position of an object can be represented by a vector, which indicates the distance from the origin of zero (coordinates $(0,0)$) in the direction in which the object is located. Both coordinates are measured as a positive or negative amount, depending on whether the object is in the positive or negative direction of the respective axis. This position can be represented, for example, with the parameter $(x,y)$, where the scalars $x$ and $y$ indicate the distance from the origin of the object in each axis.
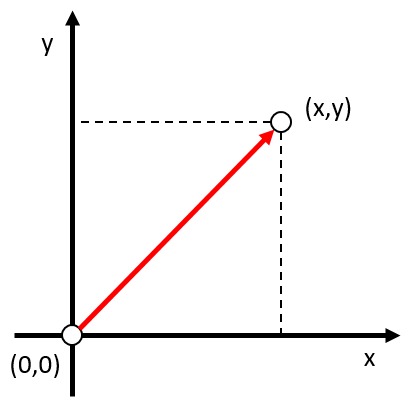
ID:(2234, 0)
Representation of the position in three dimensions
Note 
In a two-dimensional system, the position of an object can be represented by a vector, which indicates the distance from the origin of zero (coordinates $(0,0,0)$) in the direction in which the object is located. Both coordinates are measured as a positive or negative amount, depending on whether the object is in the positive or negative direction of the respective axis. This position can be represented, for example, with the parameter $(x,y,z)$, where the scalars $x$, $y$ and $z$ indicate the distance from the origin of the object in each axis.
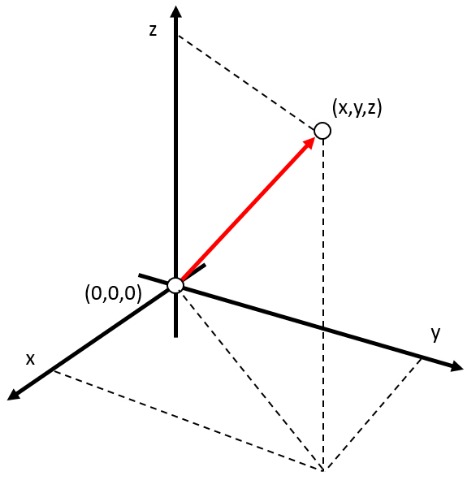
ID:(2235, 0)
Odometer
Quote 
An odometer is a device used to measure the distance traveled by a vehicle. It is typically located on the dashboard or instrument panel of a car and can be used to track the total distance traveled. An odometer works by counting the number of revolutions of a drive shaft connected to the wheels of the vehicle. As the vehicle moves, the drive shaft turns, and each revolution of the drive shaft is counted and recorded on the odometer. The odometer is typically calibrated so that it can accurately measure distances traveled in miles or kilometers.

ID:(480, 0)
Laser rangefinder
Exercise 
A laser rangefinder is a device that uses a laser beam to measure the distance between two points. It works by sending out a laser pulse, which is reflected off of the object being measured and then detected by the rangefinder. The time it takes for the laser pulse to travel from the rangefinder to the object and back can then be used to calculate the distance between the two points. Laser rangefinders are commonly used in surveying, navigation, and other applications where precise measurements are needed.

ID:(481, 0)
GPS (Global Positioning System)
Equation 
The Global Positioning System (GPS) is a satellite-based navigation system that uses a network of 24 satellites orbiting the Earth to determine the exact location of a person or object on the planet. GPS receivers calculate the distance to each satellite by measuring the amount of time it takes for signals to travel from the satellite to the receiver. Once these distances are known, the receiver can use a process called trilateration to calculate its exact location, including longitude and latitude, as well as altitude. This can be used to measure distances between two locations, as well as the length of a path taken by a person or object.

ID:(474, 0)
Distance traveled
Script 
The distance traveled in a time ($\Delta s$) by an object is measured by measuring the distance between two specific points along a trajectory. This trajectory can be a straight line on a Cartesian axis or a curved path. The distance is calculated by measuring the length of the trajectory between the two starting and ending points.
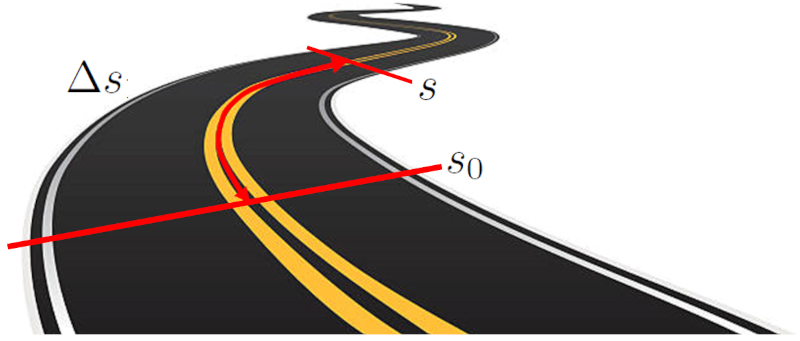
ID:(9495, 0)
Initial position in more dimensions
Variable 
The initial position of an object is its location before any movement begins. This position can be defined in more than one dimension by a vector, which goes from the origin of the coordinate system to the object, having the same number of components as the existing dimensions.
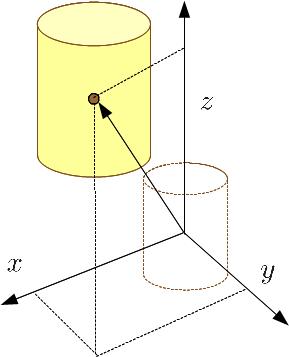
ID:(2236, 0)
Distance traveled in more dimensions
Audio 
To describe the motion of an object, it is necessary to consider the distance between its starting point and its ending point. However, this distance does not always reflect the actual distance traveled by the object, as a curved path will make the distance traveled greater than the distance between the starting and ending points. If the two points are very close together, the curvature will be negligible and therefore the distance traveled will coincide with the distance between the two points.
In this case we speak of an infinitesimal distance.
ID:(9496, 0)
Position, more dimensions
Storyboard 
To describe the position of an object in more than one dimension, it is necessary to introduce a multi-dimensional coordinate system. This system is characterized by associating a unique set of parameters with each point in space. The number of these parameters is equal to the number of dimensions. The choice of coordinate system can depend on the problem being modeled. On one hand, the aim is to have the fewest possible number of dimensions, and on the other hand, to ensure that, as much as possible, the description of motion in each dimension is independent of the other dimensions. This facilitates the solution, as each dimension can be studied separately.
Variables
Calculations
Calculations
Equations
Examples
Dimensions are the parameters needed to describe the position of a system in a particular space. These parameters can include distance, length, latitude, and height, among others. This allows a system to be located in a particular space. For example, a vehicle on a road needs only one parameter to indicate its location, while a boat on the ocean needs two parameters and an airplane three.
In a two-dimensional system, the position of an object can be represented by a vector, which indicates the distance from the origin of zero (coordinates $(0,0)$) in the direction in which the object is located. Both coordinates are measured as a positive or negative amount, depending on whether the object is in the positive or negative direction of the respective axis. This position can be represented, for example, with the parameter $(x,y)$, where the scalars $x$ and $y$ indicate the distance from the origin of the object in each axis.
In a two-dimensional system, the position of an object can be represented by a vector, which indicates the distance from the origin of zero (coordinates $(0,0,0)$) in the direction in which the object is located. Both coordinates are measured as a positive or negative amount, depending on whether the object is in the positive or negative direction of the respective axis. This position can be represented, for example, with the parameter $(x,y,z)$, where the scalars $x$, $y$ and $z$ indicate the distance from the origin of the object in each axis.
An odometer is a device used to measure the distance traveled by a vehicle. It is typically located on the dashboard or instrument panel of a car and can be used to track the total distance traveled. An odometer works by counting the number of revolutions of a drive shaft connected to the wheels of the vehicle. As the vehicle moves, the drive shaft turns, and each revolution of the drive shaft is counted and recorded on the odometer. The odometer is typically calibrated so that it can accurately measure distances traveled in miles or kilometers.
A laser rangefinder is a device that uses a laser beam to measure the distance between two points. It works by sending out a laser pulse, which is reflected off of the object being measured and then detected by the rangefinder. The time it takes for the laser pulse to travel from the rangefinder to the object and back can then be used to calculate the distance between the two points. Laser rangefinders are commonly used in surveying, navigation, and other applications where precise measurements are needed.
The Global Positioning System (GPS) is a satellite-based navigation system that uses a network of 24 satellites orbiting the Earth to determine the exact location of a person or object on the planet. GPS receivers calculate the distance to each satellite by measuring the amount of time it takes for signals to travel from the satellite to the receiver. Once these distances are known, the receiver can use a process called trilateration to calculate its exact location, including longitude and latitude, as well as altitude. This can be used to measure distances between two locations, as well as the length of a path taken by a person or object.
The distance traveled in a time ($\Delta s$) for an object is determined by measuring the distance between two specific points along a path. This path can be a straight line on a Cartesian axis or a curved trajectory. The distance is calculated as the length of the path connecting the initial and final points.
Distance traveled from an initial point to a final point
Since the value of the distance traveled in a time ($\Delta s$) is calculated as the difference between the position ($s$) and the starting position ($s_0$):
it is possible to "shift" the origin of the position by adding a constant value $d$ to both quantities:
$s \rightarrow s + d$
$s_0 \rightarrow s_0 + d$
without affecting the result of the distance traveled:
$\Delta s = s - s_0 \rightarrow (s + d) - (s_0 + d) = s - s_0 = \Delta s$
This concept is known as spatial invariance, which implies that the value of the distance traveled does not depend on the specific point where the measurement begins.
This means that the laws formulated using this principle will be spatially invariant, i.e., they will remain valid regardless of the location where the measurement is made.
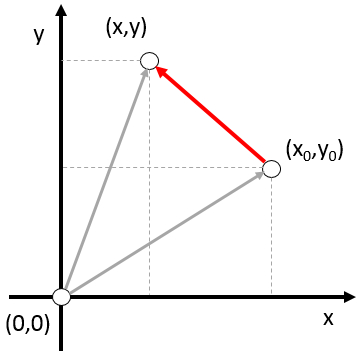
To describe the motion of an object, it is necessary to calculate the distance it has traveled. To do this, the initial and final points of the object are defined using vectors, and the distance is calculated by subtracting one vector from the other. This only coincides with the path traveled if the displacement is rectilinear, which is generally true when both points are very close, as in the case of the distance Run ($\Delta\vec{s}$) subtracting the position of Origin ($\vec{s}_0$) from the current Position ($\vec{s}$):
The initial position of an object is its location before any movement begins. This position can be defined in more than one dimension by a vector, which goes from the origin of the coordinate system to the object, having the same number of components as the existing dimensions.
To describe the motion of an object, it is necessary to consider the distance between its starting point and its ending point. However, this distance does not always reflect the actual distance traveled by the object, as a curved path will make the distance traveled greater than the distance between the starting and ending points. If the two points are very close together, the curvature will be negligible and therefore the distance traveled will coincide with the distance between the two points.
In this case we speak of an infinitesimal distance.
In the case of a space with more than one dimension, the path between two points does not necessarily have to be straight, as is the case in one-dimensional spaces. In these types of situations, a vector representing the distance between two points along the path will always be equal to or smaller than the actual distance along the path. However, they will coincide if the distance between the two points is infinitesimal or very small. Therefore, it is useful to define the infinitesimal vector, which allows us to describe the behavior of an object in a continuous space precisely.
Therefore, the path element traveled ($d\vec{s}$) is introduced as the difference between the current Position ($\vec{s}$) and the position of Origin ($\vec{s}_0$) as:
ID:(1201, 0)
