Nombre de moles
Storyboard 
Variables
Calculs
Calculs
Équations
A pression ($p$), le volume ($V$), a température absolue ($T$) et le nombre de taupes ($n$) sont li s par les lois physiques suivantes :
• Loi de Boyle
• Loi de Charles
• Loi de Gay-Lussac
• Loi d'Avogadro
Ces lois peuvent tre exprim es de mani re plus g n rale comme suit :
$\displaystyle\frac{pV}{nT}=cte$
Cette relation g n rale tablit que le produit de la pression et du volume divis par le nombre de moles et la temp rature reste constant :
Quand a pression ($p$) se comporte comme un gaz id al, en satisfaisant le volume ($V$), le nombre de taupes ($n$), a température absolue ($T$) et a constante du gaz universel ($R_C$), l' quation des gaz id aux :
et la d finition de a concentration molaire ($c_m$) :
conduisent la relation suivante :
Le nombre de taupes ($n$) correspond le nombre de particules ($N$) divis par le numéro d'Avogadro ($N_A$) :
Si nous multiplions la fois le num rateur et le d nominateur par a masse molaire ($m$), nous obtenons :
$n=\displaystyle\frac{N}{N_A}=\displaystyle\frac{Nm}{N_Am}=\displaystyle\frac{M}{M_m}$
Donc, c'est :
A pression ($p$) est associ le volume ($V$), ERROR:6679, a température absolue ($T$) et a constante du gaz universel ($R_C$) par l' quation :
Puisque ERROR:6679 peut tre calcul avec a masse ($M$) et a masse molaire ($M_m$) en utilisant :
et obtenu avec la d finition de a constante de gaz spécifique ($R_s$) en utilisant :
nous concluons que :
Si nous introduisons l' quation des gaz crite avec a pression ($p$), le volume ($V$), a masse ($M$), a constante de gaz spécifique ($R_s$) et a température absolue ($T$) comme suit :
et utilisons la d finition a densité ($\rho$) donn e par :
nous pouvons d river une quation sp cifique pour les gaz comme suit :
Dans le cas de la loi de Dalton, nous avons que a pression ($p$) est la somme de a pression partielle du composant i ($p_i$) :
Chaque composant du m lange satisfait l' quation des gaz parfaits avec a pression ($p$), le volume ($V$), le nombre de taupes ($n$), a température absolue ($T$), et a constante du gaz universel ($R_C$) :
Par cons quent, le m lange ob it galement la m me loi, o le nombre de taupes ($n$) est gal la somme de le nombre de taupes du composant i ($n_i$) :
Avec a concentration de particules ($c_n$) comme le nombre de particules ($N$) et le volume ($V$), nous obtenons :
Avec a masse molaire ($m$) et a masse ($M$),
Comme a densité ($\rho$) est
nous obtenons
$c_n=\displaystyle\frac{N}{V}=\displaystyle\frac{M}{mV}=\displaystyle\frac{\rho}{m}$
Ainsi,
Exemples
Un gaz dans lequel ses particules n'interagissent pas est connu sous le nom de gaz id al. Nous pouvons l'imaginer comme suit :
• Il se compose d'une s rie de sph res contenues l'int rieur d'un r cipient un volume ($V$).
• La vitesse de ces particules d pend de a température absolue ($T$).
• Elles g n rent une pression de ERROR:5224,0 gr ce des collisions avec les parois du r cipient.
Un gaz id al se caract rise par l'absence d'interactions potentielles entre les particules. Autrement dit, les nergies potentielles qui pourraient exister entre les particules $i$ et $j$ avec les positions $q_i$ et $q_j$ sont nulles :
En utilisant le concept de la mole, nous pouvons tablir un lien direct entre la quantit de mati re d'un gaz et le nombre de particules de le nombre de particules ($N$) pr sentes en lui. Cela simplifie les calculs et permet d' tablir une relation plus intuitive entre la quantit de gaz et ses propri t s caract ristiques, telles que a pression ($p$), le volume ($V$) et a température absolue ($T$).
La constante le numéro d'Avogadro ($N_A$), qui est approximativement gale $6,02\times 10^{23}$, est une constante fondamentale en chimie et est utilis e pour effectuer des conversions entre l' chelle macroscopique et l' chelle microscopique des atomes et des mol cules.
La valeur de ERROR:5394 peut tre calcul e partir de le nombre de particules ($N$) et a masse ($M$). Dans le premier cas, elle est obtenue en divisant par le numéro d'Avogadro ($N_A$) en utilisant la formule :
Alors que dans le deuxi me cas, a masse molaire ($M_m$) est utilis avec la formule :
Vous pouvez g n ralement calculer a masse molaire ($m$) avec a masse ($M$) et le nombre de particules ($N$) en utilisant :
ou avec a masse molaire ($M_m$) et le numéro d'Avogadro ($N_A$) en utilisant :
A concentration de particules ($c_n$) est d fini en fonction de le nombre de particules ($N$) et le volume ($V$) par :
ou en utilisant a densité ($\rho$) et a masse molaire ($m$) par :
a concentration molaire ($c_m$) est d fini en fonction de ERROR:6679 et le volume ($V$) par :
ou en utilisant a densité ($\rho$) et a masse molaire ($M_m$) par :
La relation entre les deux concentrations est le numéro d'Avogadro ($N_A$) par :
Les quations des gaz en g n ral impliquent a pression ($p$), le volume ($V$), a température absolue ($T$), a constante du gaz universel ($R_C$) et une mesure de la quantit .
Cette mesure peut tre g n rique en utilisant la loi de Dalton o seul le nombre de particules importe, pas leur type.
cette fin, il existe la version qui utilise ERROR:6679 :
et a concentration molaire ($c_m$) :
D'autre part, si vous travaillez avec le type de mol cules, vous devriez utiliser a constante de gaz spécifique ($R_s$) au lieu de a constante du gaz universel ($R_C$) :
et calculer la quantit en utilisant a masse ($M$) :
ou a densité ($\rho$) :
Dans le cas d'un gaz id al, o il n'y a pas d'interaction entre les particules, un m lange de diff rents types de gaz se comportera comme s'il s'agissait d'une plus grande quantit du m me type de gaz.
Plus pr cis ment, si nous avons trois composants avec leurs pressions partielles respectives et que nous les m langeons, la pression totale sera la somme des pressions partielles :
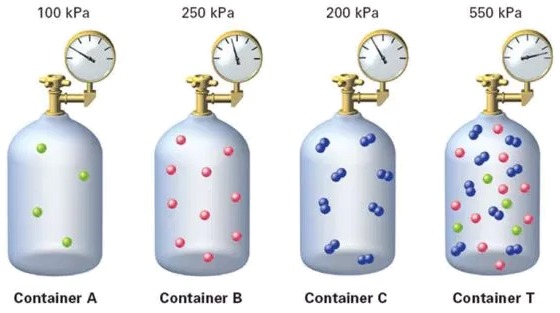
Cette image illustre comment les pressions partielles des gaz s'additionnent dans un m lange. Chaque gaz exerce une pression ind pendante et contribue la pression totale du m lange.
Ce concept est fondamental pour comprendre le comportement des m langes de gaz, car il nous permet de calculer la pression totale en fonction des pressions partielles des composants individuels.
Selon la Loi de Dalton [1], la pression totale d'un m lange de gaz est gale la somme des pressions individuelles des gaz, o une pression ($p$) est gal la somme de a pression partielle du composant i ($p_i$). Cela nous am ne conclure que le gaz se comporte comme si les particules des diff rents gaz taient identiques. De cette mani re, a pression ($p$) est la somme de a pression partielle du composant i ($p_i$) :
Par cons quent, on en conclut que le gaz se comporte comme si les diff rents gaz taient identiques et le nombre de moles correspond la somme des moles des diff rents composants :
[1] "Experimental Essays on the Constitution of Mixed Gases; on the Force of Steam or Vapour from Water and Other Liquids in Different Temperatures, Both in a Torricellian Vacuum and in Air; on Evaporation; and on the Expansion of Gases by Heat" (Essais Exp rimentaux sur la Constitution des Gaz Mixtes ; sur la Force de la Vapeur ou de la Vapeur d'Eau et d'Autres Liquides Diff rentes Temp ratures, la Fois dans un Vide de Torricelli et dans l'Air ; sur l' vaporation ; et sur l'Expansion des Gaz par la Chaleur), John Dalton, M moires de la Soci t Litt raire et Philosophique de Manchester, Volume 5, Num ro 2, Pages 535-602 (1802).
Le nombre de taupes ($n$) correspond le nombre de particules ($N$) divis par le numéro d'Avogadro ($N_A$) :
le numéro d'Avogadro ($N_A$) est une constante universelle de valeur 6.028E+23 1/mol ; elle nest donc pas incluse parmi les variables utilis es dans le calcul.
Le nombre de taupes ($n$) est d termin en divisant a masse ($M$) d'une substance par son a masse molaire ($M_m$), ce qui correspond au poids d'une mole de la substance.
Par cons quent, la relation suivante peut tre tablie :
La masse molaire est exprim e en grammes par mole (g/mol).
A masse molaire ($m$) peut tre estim partir de a masse molaire ($M_m$) et le numéro d'Avogadro ($N_A$) en utilisant
Si nous divisons a masse ($M$) par le nombre de particules ($N$), nous obtenons a masse molaire ($m$) :
Si nous divisons a densité ($\rho$) par a masse molaire ($m$), nous obtiendrons a concentration de particules ($c_n$) :
A concentration de particules ($c_n$) est d fini comme tant gal le nombre de particules ($N$) divis par le volume ($V$) :
A concentration molaire ($c_m$) correspond ERROR:9339,0 divis par le volume ($V$) d'un gaz et est calcul comme suit :
On peut calculer a concentration molaire ($c_m$) partir de a densité ($\rho$) et a masse molaire ($M_m$) comme suit :
Pour convertir a concentration molaire ($c_m$) en a concentration de particules ($c_n$), il suffit de multiplier la premi re par le numéro d'Avogadro ($N_A$), comme suit :
Lorsqu'on travaille avec les donn es sp cifiques d'un gaz, a constante de gaz spécifique ($R_s$) peut tre d fini en fonction de a constante du gaz universel ($R_C$) et a masse molaire ($M_m$) de la mani re suivante :
A pression ($p$), le volume ($V$), a température absolue ($T$) et le nombre de taupes ($n$) sont li s par l' quation suivante :
o a constante du gaz universel ($R_C$) a une valeur de 8,314 J/K mol.
A pression ($p$) peut tre calcul partir de a concentration molaire ($c_m$) en utilisant a température absolue ($T$) et a constante du gaz universel ($R_C$) de la mani re suivante :
A pression ($p$) est li a masse ($M$) avec le volume ($V$), a constante de gaz spécifique ($R_s$) et a température absolue ($T$) travers :
Si nous travaillons avec la masse ou a densité ($\rho$) du gaz, nous pouvons tablir une quation analogue celle des gaz id aux pour a pression ($p$) et a température absolue ($T$), la seule diff rence tant que la constante sera sp cifique chaque type de gaz et sera not e comme a constante de gaz spécifique ($R_s$) :
A pression totale de tous les composants ($p$) est la somme de la a pression partielle du composant i ($p_i$) i- me :
Le nombre de taupes ($n$) est gal la somme de le nombre de taupes du composant i ($n_i$) :
ID:(1477, 0)