Anzahl der Mole
Storyboard 
Im Allgemeinen hängen die idealen Gasgesetze von der Anzahl der Partikel und nicht von der Art der Partikel ab. Dies liegt daran, dass aufgrund der nicht berücksichtigten Wechselwirkung zwischen den Partikeln (ideales Gas) deren spezifische physikalische Eigenschaften keine Rolle spielen. Die Anzahl der Partikel in einem Volumen von einigen Litern Gas ist jedoch so groß ($10^{23}$), dass es kompliziert ist, mit dieser Art von Anzahl zu arbeiten. Daher wurde eine bequemere Skala definiert, indem mit den sogenannten Molen gearbeitet wurde, die Teilchen von $6.02\times 10^{23}$ entsprechen.
ID:(1477, 0)
Anzahl der Mole
Storyboard 
Im Allgemeinen hängen die idealen Gasgesetze von der Anzahl der Partikel und nicht von der Art der Partikel ab. Dies liegt daran, dass aufgrund der nicht berücksichtigten Wechselwirkung zwischen den Partikeln (ideales Gas) deren spezifische physikalische Eigenschaften keine Rolle spielen. Die Anzahl der Partikel in einem Volumen von einigen Litern Gas ist jedoch so groß ($10^{23}$), dass es kompliziert ist, mit dieser Art von Anzahl zu arbeiten. Daher wurde eine bequemere Skala definiert, indem mit den sogenannten Molen gearbeitet wurde, die Teilchen von $6.02\times 10^{23}$ entsprechen.
Variablen
Berechnungen
Berechnungen
Gleichungen
Die Druck ($p$), der Volumen ($V$), die Absolute Temperatur ($T$) und der Anzahl der Mol ($n$) stehen im Zusammenhang mit den folgenden physikalischen Gesetzen:
• Das Gesetz von Boyle
• Das Gesetz von Charles
• Das Gesetz von Gay-Lussac
• Das Gesetz von Avogadro
Diese Gesetze k nnen in einer allgemeineren Form ausgedr ckt werden:
$\displaystyle\frac{pV}{nT}=cte$
Diese allgemeine Beziehung besagt, dass das Produkt aus Druck und Volumen durch die Anzahl der Mol und die Temperatur geteilt konstant bleibt:
Wenn die Druck ($p$) sich wie ein ideales Gas verh lt und der Volumen ($V$), der Anzahl der Mol ($n$), die Absolute Temperatur ($T$) und die Universelle Gas Konstante ($R_C$) erf llt, f hrt die ideale Gasgleichung:
und die Definition von die Molare Konzentration ($c_m$):
zu folgender Beziehung:
Der Anzahl der Mol ($n$) entspricht der Anzahl der Partikel ($N$) geteilt durch der Avogadros Nummer ($N_A$):
Wenn wir sowohl den Z hler als auch den Nenner mit die Partikelmasse ($m$) multiplizieren, erhalten wir:
$n=\displaystyle\frac{N}{N_A}=\displaystyle\frac{Nm}{N_Am}=\displaystyle\frac{M}{M_m}$
Also ist es:
Die Druck ($p$) ist durch die Gleichung mit der Volumen ($V$), ERROR:6679, die Absolute Temperatur ($T$) und die Universelle Gas Konstante ($R_C$) verbunden:
Da ERROR:6679 mit die Masse ($M$) und die Molmasse ($M_m$) berechnet werden kann mittels:
und durch die Definition von die Spezifische Gaskonstante ($R_s$) mit:
folgern wir:
Wenn wir die Gleichung f r Gase einf hren, die mit die Druck ($p$), der Volumen ($V$), die Masse ($M$), die Spezifische Gaskonstante ($R_s$) und die Absolute Temperatur ($T$) geschrieben ist als:
und die Definition die Dichte ($\rho$) verwenden, die gegeben ist durch:
k nnen wir eine spezifische Gleichung f r Gase ableiten, wie folgt:
Im Fall des Dalton'schen Gesetzes haben wir, dass die Druck ($p$) die Summe von die Partialdruck der Komponente i ($p_i$) ist:
Jede Komponente des Gemischs erf llt die ideale Gasgleichung mit die Druck ($p$), der Volumen ($V$), der Anzahl der Mol ($n$), die Absolute Temperatur ($T$) und die Universelle Gas Konstante ($R_C$):
Daher entspricht das Gemisch ebenfalls demselben Gesetz, bei dem der Anzahl der Mol ($n$) gleich der Summe von der Anzahl der Mole der i-Komponente ($n_i$) ist:
Mit die Partikelkonzentration ($c_n$) als der Anzahl der Partikel ($N$) und der Volumen ($V$) erhalten wir:
Mit die Partikelmasse ($m$) und die Masse ($M$),
Da die Dichte ($\rho$) ist
erhalten wir
$c_n=\displaystyle\frac{N}{V}=\displaystyle\frac{M}{mV}=\displaystyle\frac{\rho}{m}$
Deshalb,
Beispiele
Ein Gas, in dem seine Teilchen nicht miteinander interagieren, wird als ideales Gas bezeichnet. Wir k nnen es uns folgenderma en vorstellen:
• Es besteht aus einer Reihe von Kugeln, die in einem Beh lter ein Volumen ($V$) enthalten sind.
• Die Geschwindigkeit dieser Teilchen h ngt von die Absolute Temperatur ($T$) ab.
• Sie erzeugen einen Druck von ERROR:5224,0 durch St e gegen die W nde des Beh lters.
Ein ideales Gas zeichnet sich durch das Fehlen von potenziellen Energien zwischen den Teilchen aus. Das bedeutet, dass die potenziellen Energien, die zwischen den Teilchen $i$ und $j$ mit den Positionen $q_i$ und $q_j$ existieren k nnten, null sind:
Durch die Verwendung des Konzepts des Mols k nnen wir die Menge einer Substanz in einem Gas direkt mit der Anzahl der darin enthaltenen Teilchen von der Anzahl der Partikel ($N$) in Beziehung setzen. Dies erleichtert Berechnungen und erm glicht eine intuitivere Verbindung zwischen der Menge des Gases und seinen definierenden Eigenschaften wie die Druck ($p$), der Volumen ($V$) und die Absolute Temperatur ($T$).
Die Konstante der Avogadros Nummer ($N_A$), die ungef hr $6,02\times 10^{23}$ entspricht, ist eine grundlegende Konstante in der Chemie und wird verwendet, um zwischen der makroskopischen und mikroskopischen Skala von Atomen und Molek len zu konvertieren.
Der Wert von der Número de Moles ($n$) kann aus der Anzahl der Partikel ($N$) und die Masse ($M$) berechnet werden. Im ersten Fall wird er durch der Avogadros Nummer ($N_A$) geteilt, was mit der Formel erreicht wird:
W hrend im zweiten Fall die Molmasse ($M_m$) mit der Formel verwendet wird:
Allgemein kann die Partikelmasse ($m$) mit die Masse ($M$) und der Anzahl der Partikel ($N$) berechnet werden durch:
oder mit die Molmasse ($M_m$) und der Avogadros Nummer ($N_A$) durch:
Die Konzentration von die Partikelkonzentration ($c_n$) wird in Bezug auf der Anzahl der Partikel ($N$) und der Volumen ($V$) definiert durch:
oder unter Verwendung von die Dichte ($\rho$) und die Partikelmasse ($m$) durch:
Die die Molare Konzentration ($c_m$) wird in Bezug auf ERROR:6679 und der Volumen ($V$) definiert durch:
oder unter Verwendung von die Dichte ($\rho$) und die Molmasse ($M_m$) durch:
Die Beziehung zwischen beiden Konzentrationen ist der Avogadros Nummer ($N_A$) durch:
Die Gasgleichungen im Allgemeinen beziehen sich auf die Druck ($p$), der Volumen ($V$), die Absolute Temperatur ($T$), die Universelle Gas Konstante ($R_C$) und irgendein Ma f r die Menge.
Dieses Ma kann allgemein sein und Dalton's Gesetz verwenden, bei dem nur die Anzahl der Teilchen z hlt, nicht ihr Typ.
Daf r gibt es die Version, die mit ERROR:6679 arbeitet:
und die Molare Konzentration ($c_m$):
Andererseits, wenn man mit dem Typ der Molek le arbeitet, sollte man die Spezifische Gaskonstante ($R_s$) anstelle von die Universelle Gas Konstante ($R_C$) verwenden:
und die Menge mit die Masse ($M$) berechnen:
oder die Dichte ($\rho$):
Im Fall eines idealen Gases, bei dem keine Wechselwirkungen zwischen den Teilchen auftreten, verh lt sich eine Mischung verschiedener Gase wie eine gr ere Menge desselben Gases.
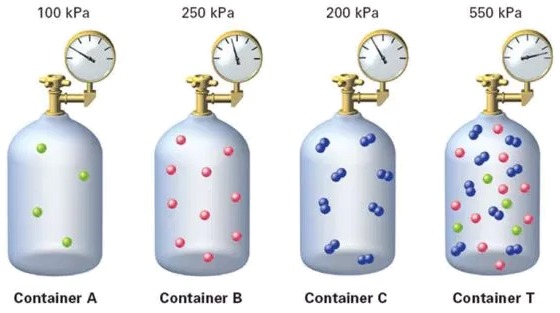
Konkret gesagt, wenn wir drei Komponenten mit ihren jeweiligen Partialdr cken haben und sie mischen, ergibt sich der Gesamtdruck als Summe der Partialdr cke:
Dieses Bild veranschaulicht, wie die Partialdr cke der Gase in einer Mischung addiert werden. Jedes Gas bt einen unabh ngigen Druck aus und tr gt zum Gesamtdruck der Mischung bei.
Dieses Konzept ist grundlegend, um das Verhalten von Gasgemischen zu verstehen, da es uns erm glicht, den Gesamtdruck basierend auf den Partialdr cken der einzelnen Komponenten zu berechnen.
Gem dem Gesetz von Dalton [1] ist der Gesamtdruck eines Gasgemisches gleich der Summe der Einzeldr cke der Gase, wobei eine Druck ($p$) gleich der Summe von die Partialdruck der Komponente i ($p_i$) ist. Dies f hrt uns zu dem Schluss, dass sich das Gas so verh lt, als w ren die Partikel der verschiedenen Gase identisch. Auf diese Weise ist die Druck ($p$) die Summe von die Partialdruck der Komponente i ($p_i$):
Daher kann man folgern, dass sich das Gas verh lt, als w ren die verschiedenen Gase identisch, und die Anzahl der Mol entspricht der Summe der Mole der verschiedenen Komponenten:
[1] "Experimental Essays on the Constitution of Mixed Gases; on the Force of Steam or Vapour from Water and Other Liquids in Different Temperatures, Both in a Torricellian Vacuum and in Air; on Evaporation; and on the Expansion of Gases by Heat" (Experimentelle Aufs tze zur Konstitution von Mischgasen; ber die Kraft von Dampf oder Dampf aus Wasser und anderen Fl ssigkeiten bei unterschiedlichen Temperaturen, sowohl im Torricellschen Vakuum als auch in der Luft; zur Verdunstung; und ber die Ausdehnung von Gasen durch W rme), John Dalton, Memoirs of the Literary and Philosophical Society of Manchester, Band 5, Ausgabe 2, Seiten 535-602 (1802).
Der Anzahl der Mol ($n$) entspricht der Anzahl der Partikel ($N$) geteilt durch der Avogadros Nummer ($N_A$):
der Avogadros Nummer ($N_A$) ist eine universelle Konstante mit dem Wert 6.028E+23 1/mol und wird daher nicht zu den im Rechenprozess verwendeten Variablen gez hlt.
Der Anzahl der Mol ($n$) wird ermittelt, indem man die Masse ($M$) einer Substanz durch ihr die Molmasse ($M_m$) teilt, was dem Gewicht eines Mols der Substanz entspricht.
Daher kann die folgende Beziehung hergestellt werden:
Die molare Masse wird in Gramm pro Mol (g/mol) ausgedr ckt.
Die Partikelmasse ($m$) kann aus die Molmasse ($M_m$) und der Avogadros Nummer ($N_A$) gesch tzt werden mithilfe von
Wenn man die Masse ($M$) durch der Anzahl der Partikel ($N$) teilt, erh lt man die Partikelmasse ($m$):
Wenn wir die Dichte ($\rho$) durch die Partikelmasse ($m$) teilen, erhalten wir die Partikelkonzentration ($c_n$):
Die Partikelkonzentration ($c_n$) wird definiert als der Anzahl der Partikel ($N$) geteilt durch der Volumen ($V$):
Die Molare Konzentration ($c_m$) entspricht ERROR:9339,0 geteilt durch der Volumen ($V$) eines Gases und wird wie folgt berechnet:
Die Molare Konzentration ($c_m$) kann von die Dichte ($\rho$) und die Molmasse ($M_m$) wie folgt berechnet werden:
Um die Molare Konzentration ($c_m$) in die Partikelkonzentration ($c_n$) umzuwandeln, multiplizieren Sie einfach die erste Zahl mit der Avogadros Nummer ($N_A$), wie folgt:
Wenn man mit den spezifischen Daten eines Gases arbeitet, kann die Spezifische Gaskonstante ($R_s$) in Abh ngigkeit von die Universelle Gas Konstante ($R_C$) und die Molmasse ($M_m$) wie folgt definiert werden:
Die Druck ($p$), der Volumen ($V$), die Absolute Temperatur ($T$) und der Anzahl der Mol ($n$) sind durch die folgende Gleichung verbunden:
wobei die Universelle Gas Konstante ($R_C$) einen Wert von 8,314 J/K mol hat.
Die Druck ($p$) kann aus die Molare Konzentration ($c_m$) unter Verwendung von die Absolute Temperatur ($T$) und die Universelle Gas Konstante ($R_C$) wie folgt berechnet werden:
Die Druck ($p$) steht in Beziehung zu die Masse ($M$) mit der Volumen ($V$), die Spezifische Gaskonstante ($R_s$) und die Absolute Temperatur ($T$) durch:
Wenn wir mit der Masse oder die Dichte ($\rho$) des Gases arbeiten, k nnen wir eine Gleichung aufstellen, die analog zu der f r ideale Gase f r die Druck ($p$) und die Absolute Temperatur ($T$) ist, wobei der einzige Unterschied darin besteht, dass die Konstante f r jeden Gastype spezifisch ist und als die Spezifische Gaskonstante ($R_s$) bezeichnet wird:
Die Gesamtdruck aller Komponenten ($p$) ist die Summe der i-ten die Partialdruck der Komponente i ($p_i$):
Der Anzahl der Mol ($n$) gleich der Summe von der Anzahl der Mole der i-Komponente ($n_i$) ist:
ID:(1477, 0)