User:
Convex Lenses
Storyboard 
Convex lenses converge the incident beam by focusing on the focal point on the side where the beam resurfaces.
ID:(1266, 0)
Convex Lens
Definition
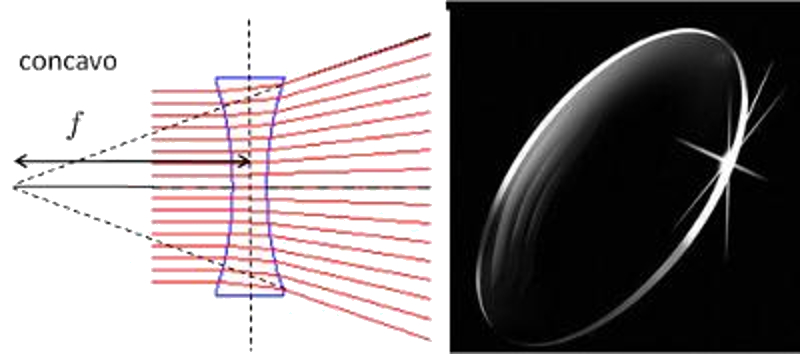
A convex lens is a lens that refracts the parallel beam of light that strikes parallel through its focus:
ID:(1855, 0)
Calculo de imagen para un lente convexo
Image
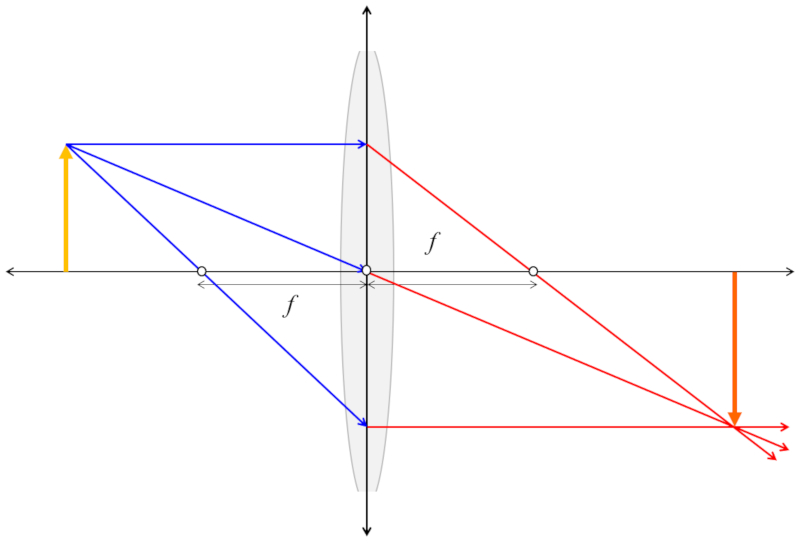
Para poder calcular el tamaño y el lugar en que se presentara la imagen se puede dibujar el eje óptico, el lente convexo y un objeto en una posición y de un tamaño. Sobre este esquema se pueden dibujar tres haces:
• Un haz paralelo al eje óptico que tras incidir sobre el lente continua por el foco del lente al otro lado de este.
• Un haz que pasa por el centro del lento continua en una linea recta al otro lado del lente.
• Un haz que pasa por el foco continua tras llegar al lente en forma paralelo al eje óptico al otro lado del lente.
Si se dibuja correctamente los tres haces se cruzaran en un punto. Dicho punto corresponde a la imagen que se crea ya que todos los haces emanan de esta. Del punto se tiene la posición, el tamaño de la imagen y si esta invertida o no.
ID:(12683, 0)
Similitud tamaños y posiciones
Note
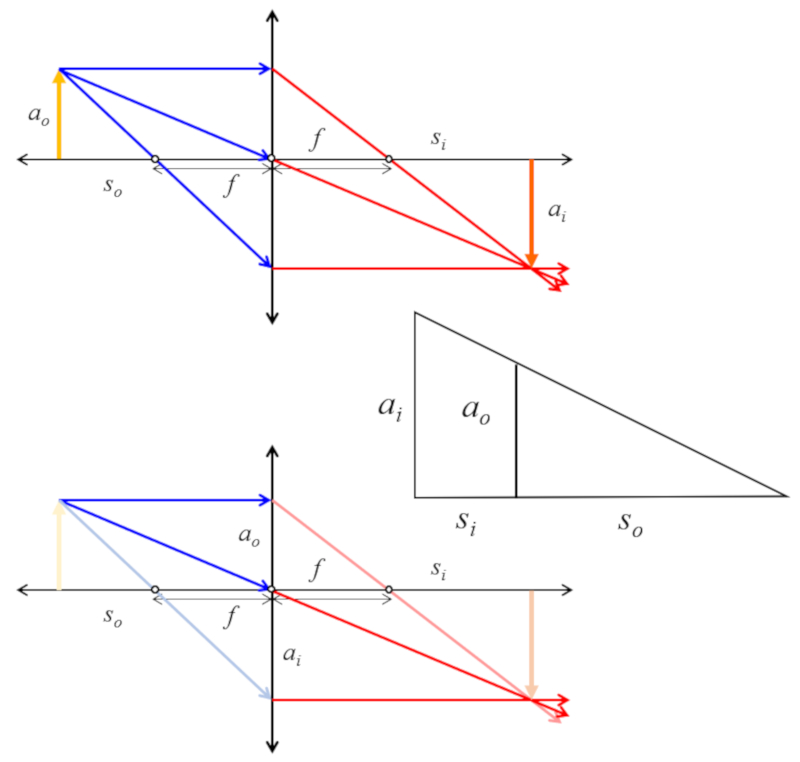
Si se consideran los triángulos del objeto e imagen se tiene que existe una similitud que se puede usar para obtener una relación de tamaños con posiciones
ID:(12697, 0)
Similitud tamaños, posición de objeto y foco
Quote
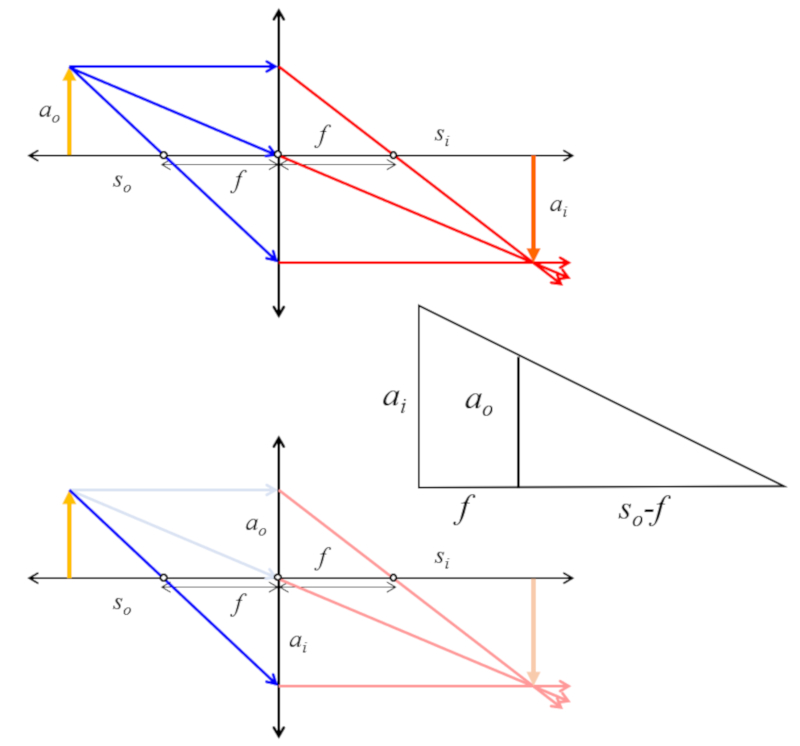
Si se consideran los triángulos del objeto e imagen se tiene que existe una similitud que se puede usar para obtener una relación de tamaños, posición del objeto y foco:
ID:(12698, 0)
Lente convexo con objeto entre origen y foco
Exercise
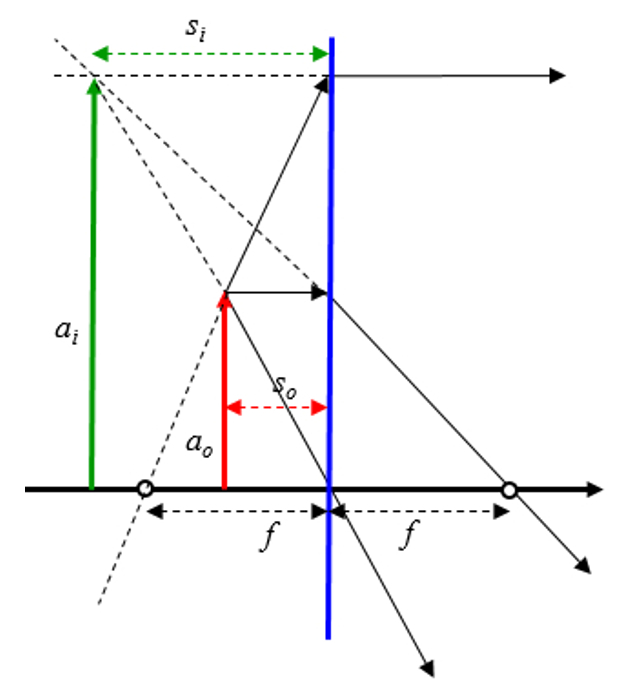
Si se asume que el objeto esta entre el origen del eje óptico y el foco se tiene:
ID:(12694, 0)
Lente convexo con objeto entre el foco y el doble del foco
Equation
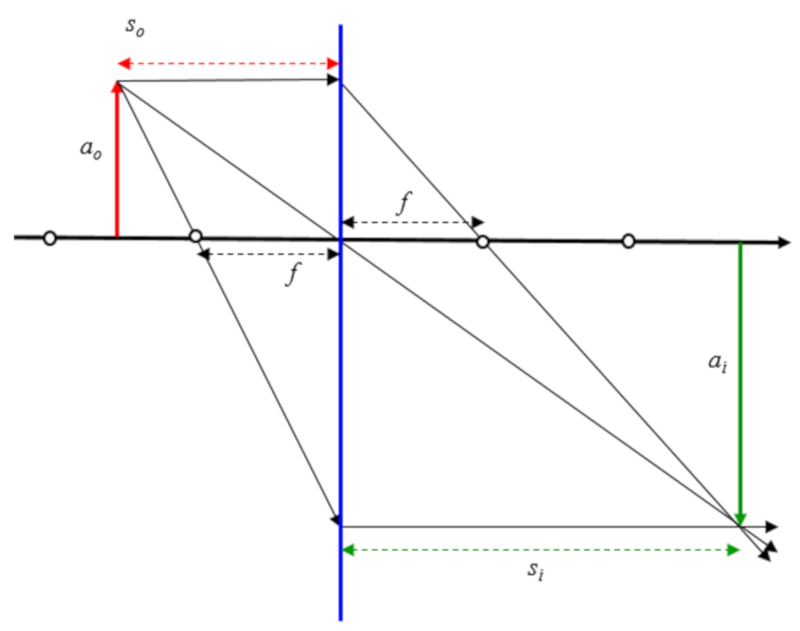
Si se asume que el objeto esta entre el origen del foco y el doble del foco se tiene:
ID:(12695, 0)
Lente convexo con objeto mas lejos que el doble del foco
Script
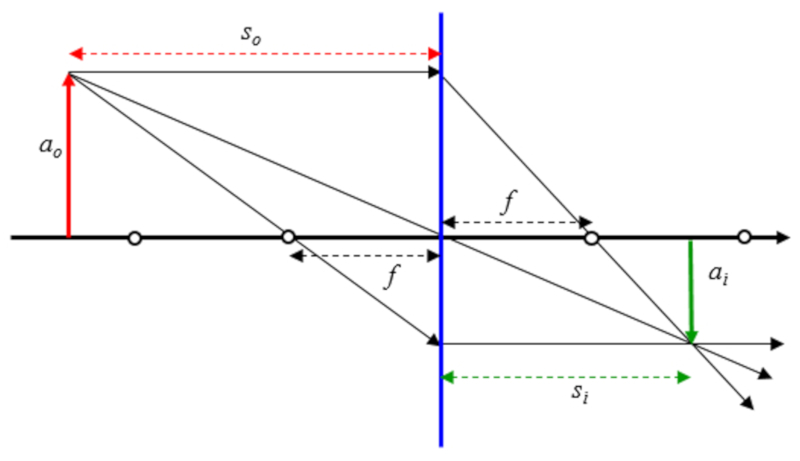
Si se asume que el objeto esta entre el origen esta mas lejos que el doble del foco se tiene:
ID:(12696, 0)
Simulación de un lente convexo
Variable
La forma como opera el lente se puede simular con
ID:(12706, 0)
Convex Lenses
Description
Convex lenses converge the incident beam by focusing on the focal point on the side where the beam resurfaces.
Variables
Calculations
to 
,
then, select the variable: 
to 
Calculations
Variable
Given
Calculate
Target :
Equation
To be used
Equations
Examples
(ID 16070)
A convex lens is a lens that refracts the parallel beam of light that strikes parallel through its focus:
(ID 1855)
Para poder calcular el tama o y el lugar en que se presentara la imagen se puede dibujar el eje ptico, el lente convexo y un objeto en una posici n y de un tama o. Sobre este esquema se pueden dibujar tres haces:
• Un haz paralelo al eje ptico que tras incidir sobre el lente continua por el foco del lente al otro lado de este.
• Un haz que pasa por el centro del lento continua en una linea recta al otro lado del lente.
• Un haz que pasa por el foco continua tras llegar al lente en forma paralelo al eje ptico al otro lado del lente.
Si se dibuja correctamente los tres haces se cruzaran en un punto. Dicho punto corresponde a la imagen que se crea ya que todos los haces emanan de esta. Del punto se tiene la posici n, el tama o de la imagen y si esta invertida o no.
(ID 12683)
Si se consideran los tri ngulos del objeto e imagen se tiene que existe una similitud que se puede usar para obtener una relaci n de tama os con posiciones
(ID 12697)
Si se consideran los tri ngulos del objeto e imagen se tiene que existe una similitud que se puede usar para obtener una relaci n de tama os, posici n del objeto y foco:
(ID 12698)
Si se asume que el objeto esta entre el origen del eje ptico y el foco se tiene:
(ID 12694)
Si se asume que el objeto esta entre el origen del foco y el doble del foco se tiene:
(ID 12695)
Si se asume que el objeto esta entre el origen esta mas lejos que el doble del foco se tiene:
(ID 12696)
La forma como opera el lente se puede simular con
(ID 12706)
(ID 16063)
La relaci n entre la proporci n de los tama os y posiciones cumple:
| $\displaystyle\frac{ s_{lv} }{ s_o }=\displaystyle\frac{ a_{lv} }{ a_o }$ |
(ID 12731)
Las posiciones de objeto e imagen y el foco se relacionan seg n la ecuaci n:
| $\displaystyle\frac{1}{ f_{lv} }=\displaystyle\frac{1}{ s_o }+\displaystyle\frac{1}{ s_{lv} }$ |
(ID 12732)
ID:(1266, 0)