Storyboard

A velocidade média é definida considerando a distância percorrida durante um intervalo de tempo decorrido, sem levar em conta as possíveis flutuações na velocidade.

Para determinar a velocidade em um instante específico, é necessário considerar um intervalo de tempo infinitesimalmente pequeno, de modo que a velocidade permaneça quase constante dentro desse intervalo.

Isso leva ao cálculo da velocidade instantânea ao computar a velocidade média no limite em que o intervalo de tempo se aproxima de zero. Matematicamente, isso corresponde à derivada da posição em relação ao tempo e representa a inclinação da curva posição-tempo.

>Modelo

ID:(1432, 0)

Definição

Por um lado, é importante diferenciar entre o caso mais simples, unidimensional, e aquele mais complexo envolvendo mais de uma dimensão. Em ambos os casos, a derivada de la posição ($s$) em relação a o tempo ($t$), que corresponde à inclinação da curva de la posição ($s$), é igual a la velocidade ($v$). Da mesma forma, a derivada de la posição (vector) ($\vec{s}$) em relação a o tempo ($t$), corresponde a la velocidade (vector) ($\vec{v}$).

Por outro lado, a área sob a curva de la velocidade ($v$) em o tempo ($t$), que corresponde à integração, nos permite calcular la posição ($s$).

ID:(15393, 0)

Imagem

La velocidade ($v$) é definido como o deslocamento por unidade de tempo. No entanto, esse conceito se reduz a uma velocidade média ($\bar{v}$) que existe durante o intervalo de tempo considerado.

A limitação da velocidade média é refletida no fato de que se assume que um objeto passa instantaneamente do repouso para ter uma velocidade dada. É como se um ônibus, assim que sai do terminal, passasse a ter uma velocidade constante, o que é totalmente absurdo. A velocidade evolui, aumenta, diminui (semáforo, passageiros subindo) e lentamente aumenta até atingir um valor mais ou menos constante quando viaja em uma estrada. Assim, um ônibus que normalmente viaja a 100 km/h na estrada levará mais de 8 horas para percorrer 800 km, pois as flutuações de velocidade devem ser consideradas. No final, terá levado 10 horas para percorrer 800 km, viajando a uma velocidade média de 80 km/h.

Se deseja conhecer a velocidade em cada instante, deve-se considerar um intervalo de tempo tão pequeno que, durante este intervalo, a velocidade pode ser considerada aproximadamente constante. Com isso, a velocidade média estimada desta forma equivale à velocidade existente no instante considerado.

Por isso, falamos de velocidade instantânea.

ID:(16, 0)

Nota

Se tomarmos um tempo ($t$) com uma posição ($s$) ($s(t)$) e observarmos um ponto em um tempo futuro $t+\Delta t$ com uma posição $s(t+\Delta t)$, podemos estimar a velocidade como a distância percorrida no tempo $\Delta t$:

$s(t+\Delta t)-s(t)$

la velocidade ($v$) pode ser calculado dividindo a distância percorrida pelo tempo decorrido:

$v\sim\displaystyle\frac{s(t+\Delta t)-s(t)}{\Delta t}$

À medida que o valor de $\Delta t$ diminui, a velocidade calculada se aproxima da tangente à curva de posição no tempo:

Isso generaliza o que já foi visto para o caso de velocidade constante.

ID:(1638, 0)

Citar

A integral de la velocidade ($v$) corresponde à área sob a curva que define essa função. Portanto, a integral da velocidade entre o tempo inicial ($t_0$) e o tempo ($t$) corresponde à distância percorrida entre la velocidade ($s_0$) e la posição ($s$).

Portanto, temos:



O que é representado no seguinte gráfico:

ID:(2242, 0)

Exercício

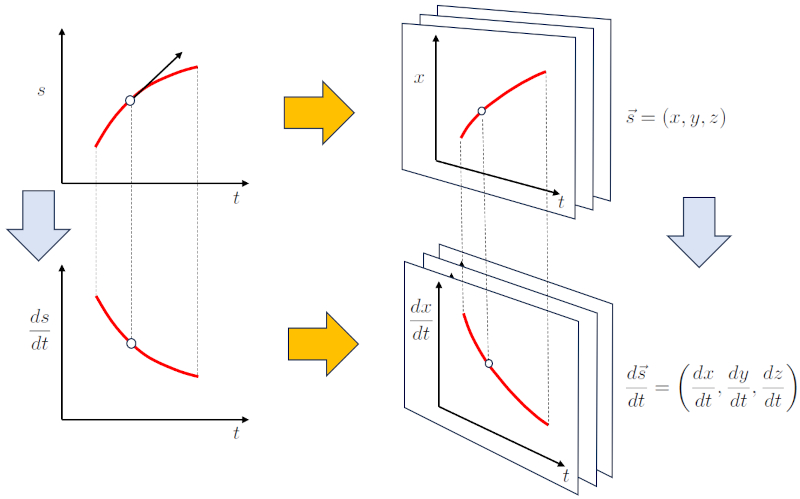
Para movimentos que ocorrem em mais de uma dimensão, a descrição do movimento em uma dimensão deve ser generalizada. Isso é alcançado trabalhando com uma versão de múltiplas dimensões para a posição. No caso de três dimensões, isso é representado por:

$s \rightarrow \vec{s} = (x, y, z)$

De forma análoga, a derivada do vetor no tempo pode ser definida, o que resulta no vetor velocidade:

$v=\displaystyle\frac{ds}{dt} \rightarrow \displaystyle\frac{d\vec{s}}{dt} = \left(\displaystyle\frac{dx}{dt}, \displaystyle\frac{dy}{dt}, \displaystyle\frac{dz}{dt}\right) = (v_x, v_y, v_z) = \vec{v}$

Isso pode ser resumido na seguinte representação gráfica:

ID:(15506, 0)

Equação

No caso de uma dimensão, la velocidade ($v$) está relacionada com la posição ($s$) através de sua derivada em o tempo ($t$), enquanto a integral de la velocidade ($v$) no intervalo de o tempo ($t$) a o tempo inicial ($t_0$) fornece la posição ($s$) a partir de la velocidade ($s_0$). Em um contexto mais geral, em mais de uma dimensão, a função la posição (vector) ($\vec{s}$) pode ser derivada em o tempo ($t$), resultando em la velocidade (vector) ($\vec{v}$).

ID:(15391, 0)