Storyboard

La velocidad media se define teniendo en cuenta la distancia recorrida en un intervalo de tiempo, sin tomar en consideración las posibles fluctuaciones de la velocidad.

Para determinar la velocidad en un instante específico, es necesario considerar un intervalo de tiempo extremadamente pequeño de modo que la velocidad no tenga variaciones notables en ese período.

Por esta razón, se obtiene la velocidad instantánea calculando la velocidad media en el límite de un intervalo de tiempo que tiende a cero. Desde el punto de vista matemático, esto equivale a la derivada de la posición respecto al tiempo y a la pendiente de la curva posición-tiempo.

>Modelo

ID:(1432, 0)

Definición

Por un lado, es importante diferenciar entre el caso más simple, unidimensional, y aquel de más de una dimensión. Para ambos casos, la derivada de la posición ($s$) en el tiempo ($t$), que corresponde a la pendiente de la curva de la posición ($s$), es igual a la velocidad ($v$). De manera similar, la derivada de la posición (vector) ($\vec{s}$) en el tiempo ($t$), que corresponde a la velocidad (vector) ($\vec{v}$).

Por otro lado, el área debajo de la curva de la velocidad ($v$) en el tiempo ($t$), que corresponde a la integración, nos permite calcular la posición ($s$).

ID:(15393, 0)

Imagen

La velocidad ($v$) se define como el desplazamiento por unidad de tiempo. Sin embargo, este concepto se reduce a una velocidad media ($\bar{v}$) que existe durante el intervalo de tiempo considerado.

La limitación de la velocidad media se refleja en el hecho de que se asume que un objeto pasa instantáneamente del reposo a una velocidad determinada. Por ejemplo, un autobús que acaba de salir de la terminal no alcanza inmediatamente su velocidad de crucero, lo que es completamente absurdo. La velocidad evoluciona, aumenta, disminuye (semáforos, subida de pasajeros) y aumenta gradualmente hasta alcanzar un valor más o menos constante cuando viaja por carretera. Por lo tanto, un autobús que normalmente viaja a unos 100 km/h en carretera tardará más de 8 horas en recorrer 800 km, ya que se deben considerar las fluctuaciones de velocidad. Al final, habrá tardado 10 horas en recorrer 800 km a una velocidad media de 80 km/h.

Si se desea conocer la velocidad en cada instante, se debe tomar un intervalo de tiempo lo suficientemente pequeño para que durante ese tiempo la velocidad se pueda considerar aproximadamente constante. De esta manera, la velocidad media estimada de esta forma equivale a la velocidad existente en el instante considerado.

Por lo tanto, hablamos de la velocidad instantánea para referirnos a la velocidad en un momento determinado.

ID:(16, 0)

Nota

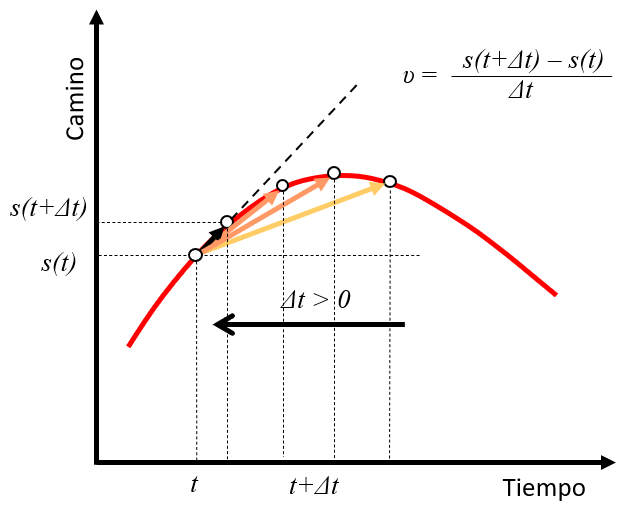
Si consideramos un tiempo ($t$) con una posición ($s$) ($s(t)$) y observamos un punto en un tiempo futuro $t+\Delta t$ con una posición $s(t+\Delta t)$, podemos estimar la velocidad como el desplazamiento en el tiempo $\Delta t$:

$s(t+\Delta t)-s(t)$

la velocidad ($v$) se puede calcular dividiendo la distancia recorrida por el tiempo transcurrido:

$v\sim\displaystyle\frac{s(t+\Delta t)-s(t)}{\Delta t}$

A medida que el valor de $\Delta t$ se hace más pequeño, la velocidad calculada se aproxima a la tangente a la curva de posición en el tiempo:

Autopista con salida

Esto generaliza lo que ya se había visto para el caso de velocidad constante.

ID:(1638, 0)

Cita

La integral de la velocidad ($v$) corresponde al área bajo la curva que define dicha función. Por lo tanto, la integral de la velocidad entre el tiempo inicial ($t_0$) y el tiempo ($t$) corresponde al camino recorrido entre la posición inicial ($s_0$) y la posición ($s$).

Por lo tanto, se tiene:



Lo cual se representa en la siguiente gráfica:

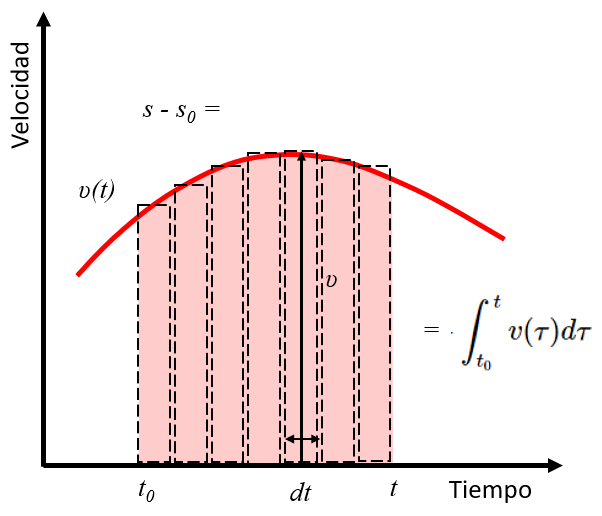
Camino como área debajo de la curva velocidad y tiempo.

ID:(2242, 0)

Ejercicio

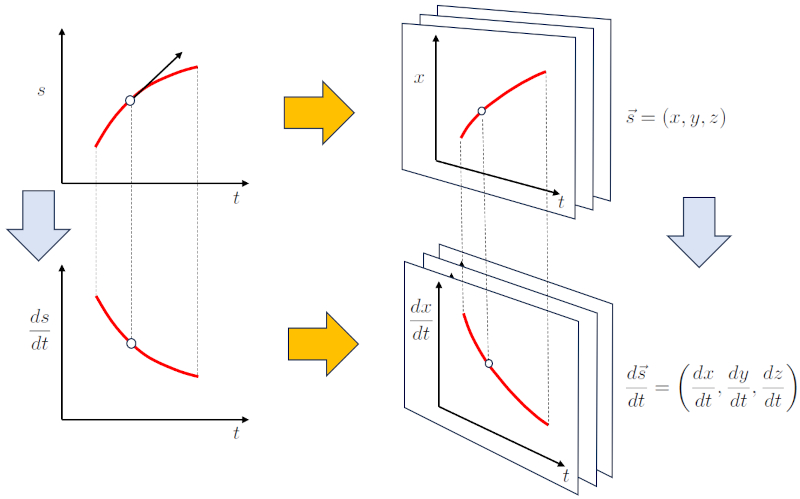
Para movimientos que ocurren en más de una dimensión, la descripción del movimiento en una dimensión debe ser generalizada. Esto se logra trabajando con una versión de más dimensiones para la posición. En el caso de tres dimensiones, esto es:

$s \rightarrow \vec{s} = (x, y, z)$

De manera análoga, se puede definir la derivada del vector respecto al tiempo, lo que da origen al vector de velocidad:

$v=\displaystyle\frac{ds}{dt} \rightarrow \displaystyle\frac{d\vec{s}}{dt} = \left(\displaystyle\frac{dx}{dt}, \displaystyle\frac{dy}{dt}, \displaystyle\frac{dz}{dt}\right) = (v_x, v_y, v_z) = \vec{v}$

Esto se resume en la siguiente representación gráfica:

ID:(15506, 0)

Ecuación

En el caso de una dimensión, la velocidad ($v$) está relacionada con la posición ($s$) a través de su derivada en el tiempo ($t$), mientras que la integral de la velocidad ($v$) en el intervalo el tiempo ($t$) a partir de el tiempo inicial ($t_0$) proporciona la posición ($s$) desde la posición inicial ($s_0$). En un contexto más general, en más de una dimensión, la función de la posición (vector) ($\vec{s}$) puede ser derivada en el tiempo ($t$), lo que resulta en la velocidad (vector) ($\vec{v}$).

ID:(15391, 0)