Storyboard

In the case of a pendulum it is gravity that generates a torque opposite to the mass leaving the resting point. However, the torque is not proportional to the angle, there being a non-linear relationship which makes the movement more complex.

Since the torque is not proportional to the angle, the oscillation frequency depends on the amplitude, which makes it difficult to apply it to mark the passage on a clock. However, the effect is minimal if the angle is small which leads to the application of the pendulum on clocks is achieved with long bars.

>Model

ID:(1426, 0)

Description

>Top

When a pendulum of length $l$ is deflected at an angle $\theta$, the mass gains height, which is calculated as

$l - l \cos\theta = l (1 - \cos\theta)$

this is associated with the gain in gravitational potential energy.

ID:(1239, 0)

Equation

>Top, >Model

For a pendulum with length $L$ that is deflected at an angle $\theta$, the mass is raised

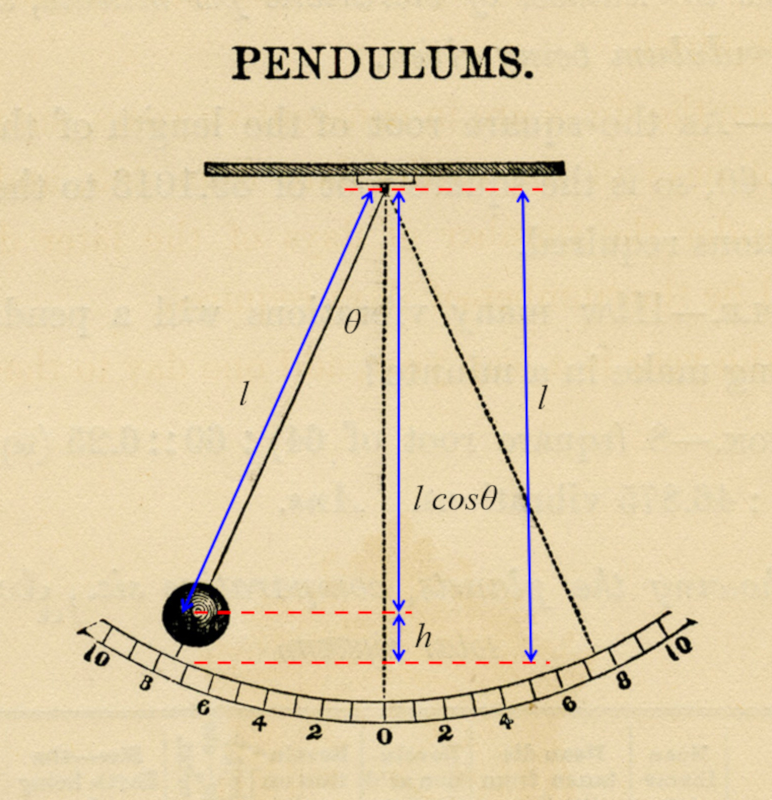
by a height equal to:

$ h = L (1-\cos \theta )$

Conditions

Variables

$h$

Height in Case Pendulum

$m$

6296

$L$

Pendulum Length

$m$

6282

$\theta$

Swing angle

$rad$

6283

Relation

ID:(4523, 0)

Equation

>Top, >Model

For the case of a mass $m$ hanging from a string of length $L$ and being deflected at an angle $\theta$ from the vertical, the mass will gain a height of

which means that the gravitational potential energy

will be

$ U = m g L (1-\cos \theta )$

Conditions

Variables

$g$

Gravitational Acceleration

9.8

$m/s^2$

5310

$m_g$

Gravitational mass

$kg$

8762

$L$

Pendulum Length

$m$

6282

$U$

Potential Energy Pendulum

$J$

6284

$\theta$

Swing angle

$rad$

6283

Relation

where $g$ is the acceleration due to gravity.

ID:(4513, 0)

Equation

>Top, >Model

The gravitational potential energy of a pendulum is

which for small angles can be approximated as:

$ V =\displaystyle\frac{1}{2} m_g g L \theta ^2$

Conditions

Variables

$g$

Gravitational Acceleration

9.8

$m/s^2$

5310

$m_g$

Gravitational mass

$kg$

8762

$L$

Pendulum Length

$m$

6282

$V$

Potential Energy Pendulum, for small Angles

$J$

6285

$\theta$

Swing angle

$rad$

6283

Relation

Development

The gravitational potential energy of a pendulum with mass m, suspended from a string of length L and deflected by an angle \theta is given by

$ U = m g L (1-\cos \theta )$

where g is the acceleration due to gravity.

For small angles, the cosine function can be approximated using a Taylor series expansion up to the second term

$\cos\theta\sim 1-\displaystyle\frac{1}{2}\theta^2$

This approximation leads to the simplification of the potential energy to

$ V =\displaystyle\frac{1}{2} m_g g L \theta ^2$

It's important to note that the angle must be expressed in radians.

ID:(4514, 0)