Benützer:


Pendelschaukel
Storyboard

Im Falle eines Pendels ist es die Schwerkraft, die ein Drehmoment erzeugt, das der Masse entgegengesetzt ist, die den Ruhepunkt verlässt. Das Drehmoment ist jedoch nicht proportional zum Winkel, da es eine nichtlineare Beziehung gibt, die die Bewegung komplexer macht.

Da das Drehmoment nicht proportional zum Winkel ist, hängt die Oszillationsfrequenz von der Amplitude ab, was es schwierig macht, sie anzuwenden, um den Durchgang auf einer Uhr zu markieren. Der Effekt ist jedoch minimal, wenn der Winkel klein ist, was dazu führt, dass die Anbringung des Pendels an Uhren mit langen Stäben erreicht wird.

>Modell

ID:(1426, 0)


Berechnung der potentiellen Energie des Pendulum
Definition

Wenn ein Pendel der Länge $l$ um einen Winkel $\theta$ abgelenkt wird, gewinnt die Masse an Höhe, die berechnet wird als

$l - l \cos\theta = l (1 - \cos\theta)$

dies ist mit dem Gewinn an potentieller Gravitationsenergie verbunden.

ID:(1239, 0)


Pendelschaukel
Beschreibung

Im Falle eines Pendels ist es die Schwerkraft, die ein Drehmoment erzeugt, das der Masse entgegengesetzt ist, die den Ruhepunkt verlässt. Das Drehmoment ist jedoch nicht proportional zum Winkel, da es eine nichtlineare Beziehung gibt, die die Bewegung komplexer macht. Da das Drehmoment nicht proportional zum Winkel ist, hängt die Oszillationsfrequenz von der Amplitude ab, was es schwierig macht, sie anzuwenden, um den Durchgang auf einer Uhr zu markieren. Der Effekt ist jedoch minimal, wenn der Winkel klein ist, was dazu führt, dass die Anbringung des Pendels an Uhren mit langen Stäben erreicht wird.

Variablen
Symbol
Text
Variable
Wert
Einheiten
Berechnen
MKS-Wert
MKS-Einheiten
$m_g$
m_g
Gravitationsmasse
kg
$h$
h
Höhe in der Rechtssache Pendulum
m
$L$
L
Pendel Länge
m
$V$
V
Potenzielle Energie Pendulum
J
$V$
V
Potenzielle Energie Pendulum, für kleine Winkel
J
$\theta$
theta
Schwenkwinkel
rad

Berechnungen

Zuerst die Gleichung auswählen:   zu ,  dann die Variable auswählen:   zu 
Symbol
Gleichung
Gelöst
Übersetzt

Berechnungen

Symbol
Gleichung
Gelöst
Übersetzt

 Variable   Gegeben   Berechnen   Ziel :   Gleichung   Zu verwenden


Gleichungen

Die potenzielle Gravitationsenergie eines Pendels mit Masse m, das an einem Faden der L nge L aufgeh ngt ist und um einen Winkel \theta ausgelenkt wird, ist gegeben durch

$ U = m g L (1-\cos \theta )$



wobei g die Erdbeschleunigung ist.

F r kleine Winkel kann die Kosinus-Funktion durch eine Taylor-Reihenentwicklung bis zur zweiten Ordnung approximiert werden

$\cos\theta\sim 1-\displaystyle\frac{1}{2}\theta^2$



Diese N herung f hrt zu einer Vereinfachung der potenziellen Energie zu

$ V =\displaystyle\frac{1}{2} m_g g L \theta ^2$

(ID 4514)

Beispiele

Wenn ein Pendel der L nge $l$ um einen Winkel $\theta$ abgelenkt wird, gewinnt die Masse an H he, die berechnet wird als

$l - l \cos\theta = l (1 - \cos\theta)$

dies ist mit dem Gewinn an potentieller Gravitationsenergie verbunden.

(ID 1239)

F r ein Pendel der L nge $L$, das um einen Winkel $\theta$ ausgelenkt wird, wird die Masse angehoben



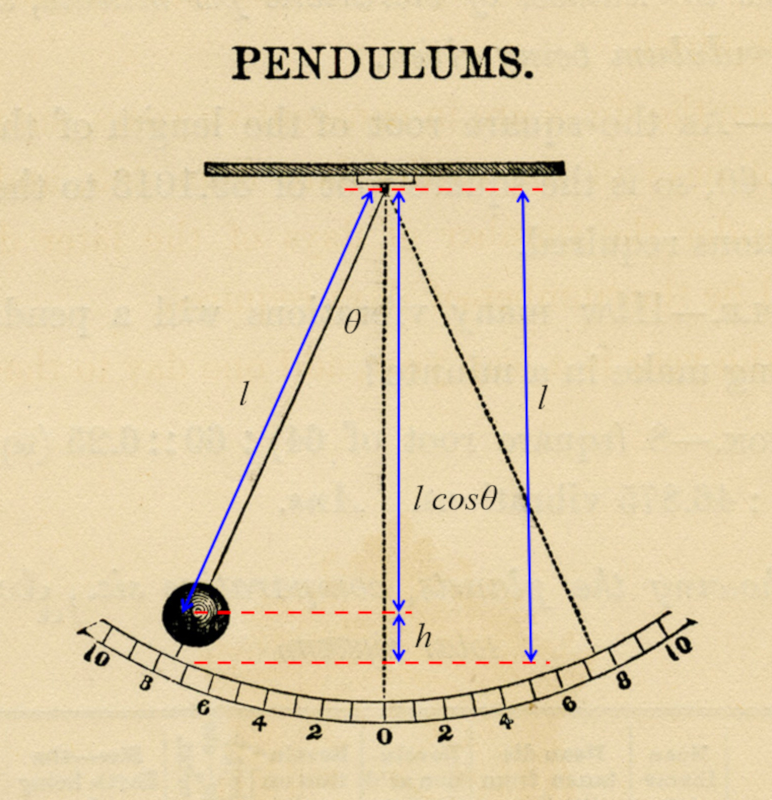
auf eine H he, die gleich ist zu:

$ h = L (1-\cos \theta )$

(ID 4523)

Im Fall einer Masse $m$, die an einem Seil der L nge $L$ h ngt und um einen Winkel $\theta$ von der Vertikalen abgelenkt wird, gewinnt die Masse eine H he von

$ h = L (1-\cos \theta )$



was bedeutet, dass die potenzielle gravitative Energie

$ V = - m_g g z $



sein wird

$ U = m g L (1-\cos \theta )$

wobei $g$ die Erdbeschleunigung ist.

(ID 4513)

Die potenzielle Gravitationsenergie eines Pendels ist

$ U = m g L (1-\cos \theta )$



die f r kleine Winkel approximiert werden kann als:

$ V =\displaystyle\frac{1}{2} m_g g L \theta ^2$



Es ist wichtig zu beachten, dass der Winkel in Radiant angegeben sein muss.

(ID 4514)

ID:(1426, 0)