Energía cinetica de rotación y momentos de inercia
Storyboard 
La energía cinética de rotación es una función de la velocidad angular alcanzada mediante la aplicación de un torque durante un cierto tiempo mientras se recorre un ángulo dado.
Por lo tanto, la energía cinética rotacional es proporcional al momento de inercia del objeto y al cuadrado de la velocidad angular.
ID:(1417, 0)
Barra que rota en torno a un eje $\perp$
Imagen 
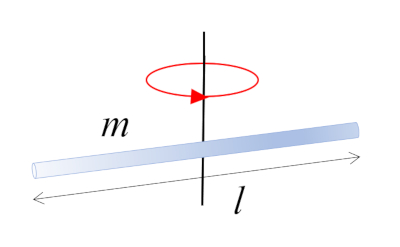
Una barra de masa $m$ y longitud $l$ que gira alrededor de su centro, que coincide con el centro de masa:
ID:(10962, 0)
Cilindro que rota en torno a eje $\parallel$
Nota 
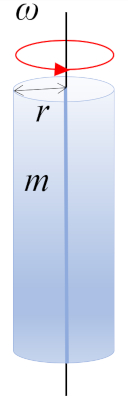
Una rotación de un cilindro con masa $m$ y radio $r$ alrededor del eje del cilindro, donde el centro de masa (CM) se encuentra a media altura:
ID:(10964, 0)
Cilindro que rota en torno a eje $\perp$
Cita 
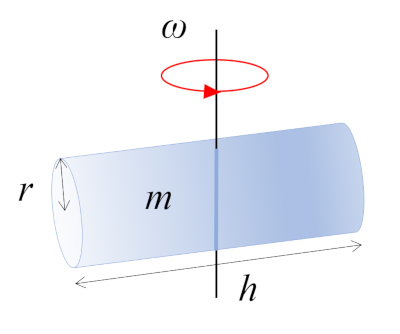
En esta situación, un cilindro con masa $m$, radio $r$ y altura $h$ está girando alrededor de un eje que es perpendicular a su propio eje. Este eje pasa por el punto medio de la longitud del cilindro, donde se localiza el centro de masa (CM):
ID:(10965, 0)
Esfera
Ejercicio 
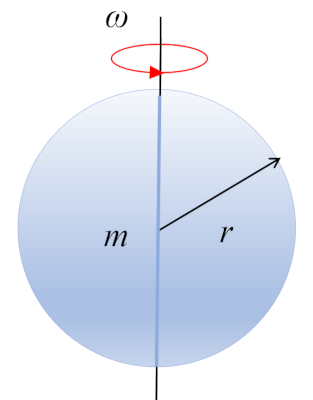
Una esfera con masa $m$ y radio $r$ está girando alrededor de su centro de masa, el cual se encuentra en el centro de la esfera:
ID:(10490, 0)
Momento de inercia de paralelepípedo regular
Ecuación 
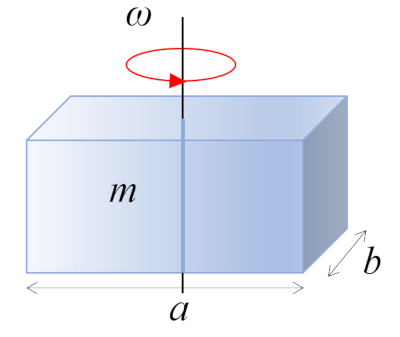
Un paralelepípedo rectángulo con masa $m$, lados $a$ y $b$, y perpendicular al eje de rotación, está girando alrededor de su centro de masa, que se encuentra en el centro geométrico del cuerpo:
ID:(10973, 0)
Paralelepípedo recto
Script 
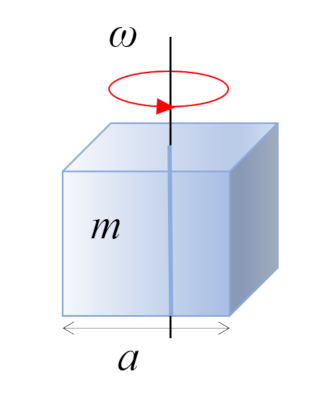
Para un paralelepípedo recto con masa $m$ y lado $a$, el centro de masa se encuentra en el centro geométrico:
ID:(10963, 0)
Momento de inercia
Descripción 
En la dinámica rotacional, el momento de inercia cumple el rol equivalente al de la masa inercial en la traslación. Sin embargo, a diferencia de la masa, el momento de inercia depende de la geometría del cuerpo y de cómo se distribuye su masa con respecto al eje de rotación. Por ello, su cálculo es imprescindible para cada caso que se pretenda modelar.
Variables
Cálculos
Cálculos
Ecuaciones
La variación del trabajo ($\Delta W$) necesaria para que un objeto cambie de la velocidad angular inicial ($\omega_0$) a la velocidad angular ($\omega$) se obtiene aplicando un el torque ($T$) que produce un desplazamiento angular la diferencia de ángulos ($\Delta\theta$), según:
| $ \Delta W = T \Delta\theta $ |
Aplicando la segunda ley de Newton para la rotación, en función de el momento de inercia para eje que no pasa por el CM ($I$) y la aceleración angular media ($\bar{\alpha}$):
| $ T = I \alpha $ |
esta expresión puede reescribirse como:
$\Delta W = I \alpha \Delta\theta$
o, utilizando la diferencia de velocidades angulares ($\Delta\omega$) y el tiempo transcurrido ($\Delta t$):
| $ \bar{\alpha} \equiv \displaystyle\frac{ \Delta\omega }{ \Delta t }$ |
obtenemos:
$\Delta W = I\displaystyle\frac{\Delta\omega}{\Delta t} \Delta\theta$
Si utilizamos la definición de la velocidad angular media ($\bar{\omega}$) y el tiempo transcurrido ($\Delta t$):
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
resulta:
$\Delta W = I\displaystyle\frac{\Delta\omega}{\Delta t} \Delta\theta = I\omega \Delta\omega$
donde la diferencia de velocidades angulares ($\Delta\omega$) se expresa como:
| $ \Delta\omega = \omega_2 - \omega_1 $ |
Por otro lado, la velocidad angular puede aproximarse mediante la velocidad angular promedio:
$\bar{\omega}=\displaystyle\frac{\omega_1 + \oemga_2}{2}$
Combinando ambas expresiones, se obtiene la ecuación:
$\Delta W = I \omega \Delta\omega = I(\omega_2 - \omega_1) \displaystyle\frac{(\omega_1 + \omega_2)}{2} = \displaystyle\frac{I}{2}(\omega_2^2 - \omega_1^2)$
Por lo tanto, el cambio en la energía se expresa como:
$\Delta W = \displaystyle\frac{I}{2}\omega_2^2 - \displaystyle\frac{I}{2}\omega_1^2$
Lo que nos permite definir la energía cinética rotacional como:
| $ K_r =\displaystyle\frac{1}{2} I \omega ^2$ |
(ID 3255)
El momento de inercia de una barra en rotaci n alrededor de un eje perpendicular ($\perp$) que pasa por el centro se obtiene al dividir el cuerpo en peque os vol menes y sumarlos:
| $ I =\displaystyle\int_V r ^2 \rho dV $ |
lo que resulta en
| $ I_{CM} =\displaystyle\frac{1}{12} m l ^2$ |
.
(ID 4432)
El momento de inercia de un paralelep pedo en rotaci n alrededor de un eje que pasa por el centro se obtiene al dividir el cuerpo en peque os vol menes y luego sumarlos:
| $ I =\displaystyle\int_V r ^2 \rho dV $ |
esto da como resultado
| $ I_{CM} =\displaystyle\frac{1}{12} m ( a ^2+ b ^2)$ |
.
(ID 4433)
El momento de inercia de un cilindro que rota alrededor de un eje paralelo ($\parallel$) que pasa por el centro se calcula al dividir el cuerpo en peque os vol menes y sumarlos:
| $ I =\displaystyle\int_V r ^2 \rho dV $ |
lo que resulta en
| $ I_{CM} =\displaystyle\frac{1}{2} m r_c ^2$ |
.
(ID 4434)
El momento de inercia de un cilindro que gira alrededor de un eje perpendicular ($\perp$) que pasa por el centro se calcula al dividir el cuerpo en peque os vol menes y sumarlos:
| $ I =\displaystyle\int_V r ^2 \rho dV $ |
lo que resulta en
| $ I_{CM} =\displaystyle\frac{1}{12} m ( h ^2+3 r_c ^2)$ |
.
(ID 4435)
El momento de inercia de una esfera en rotaci n alrededor de un eje que atraviesa su centro se obtiene mediante la segmentaci n del cuerpo en peque os vol menes y sumando:
| $ I =\displaystyle\int_V r ^2 \rho dV $ |
lo que resulta en
| $ I_{CM} =\displaystyle\frac{2}{5} m r_e ^2$ |
.
(ID 4436)
Ejemplos
(ID 15604)
Una barra de masa $m$ y longitud $l$ que gira alrededor de su centro, que coincide con el centro de masa:

(ID 10962)
Una rotaci n de un cilindro con masa $m$ y radio $r$ alrededor del eje del cilindro, donde el centro de masa (CM) se encuentra a media altura:

(ID 10964)
En esta situaci n, un cilindro con masa $m$, radio $r$ y altura $h$ est girando alrededor de un eje que es perpendicular a su propio eje. Este eje pasa por el punto medio de la longitud del cilindro, donde se localiza el centro de masa (CM):

(ID 10965)
Una esfera con masa $m$ y radio $r$ est girando alrededor de su centro de masa, el cual se encuentra en el centro de la esfera:

(ID 10490)
Un paralelep pedo rect ngulo con masa $m$, lados $a$ y $b$, y perpendicular al eje de rotaci n, est girando alrededor de su centro de masa, que se encuentra en el centro geom trico del cuerpo:

(ID 10973)
Para un paralelep pedo recto con masa $m$ y lado $a$, el centro de masa se encuentra en el centro geom trico:

(ID 10963)
(ID 15606)
El momento de inercia para eje que no pasa por el CM ($I$) se puede calcular utilizando el momento de inercia del centro de masa ($I_{CM}$) y sum ndole el momento de inercia de la masa del cuerpo ($m$) como si fuera una masa puntual en la distancia centro de masa y eje ($d$):
| $ I = I_{CM} + m d ^2$ |
(ID 3688)
El momento de Inercia CM de una Barra delgada, eje perpendicular ($I_{CM}$) se obtiene en función de la masa del cuerpo ($m$) y el largo de barra delgada ($l$):
| $ I_{CM} =\displaystyle\frac{1}{12} m l ^2$ |
(ID 4432)
El momento de Inercia CM de un Cilindro, eje paralelo a eje cilindro ($I_{CM}$) se obtiene en función de la masa del cuerpo ($m$) y el radio de cilindro ($r_c$):
| $ I_{CM} =\displaystyle\frac{1}{2} m r_c ^2$ |
(ID 4434)
El momento de Inercia CM de un Cilindro, eje perpendicular a eje cilindro ($I_{CM}$) se obtiene en función de la masa del cuerpo ($m$), la altura de cilindro ($h$) y el radio de cilindro ($r_c$):
| $ I_{CM} =\displaystyle\frac{1}{12} m ( h ^2+3 r_c ^2)$ |
(ID 4435)
El momento de Inercia CM de un Cilindro, eje perpendicular a eje cilindro ($I_{CM}$) se obtiene en función de la masa del cuerpo ($m$), el largo de la arista de un paralelepípedo recto ($a$) y el ancho de la arista de un paralelepípedo recto ($b$):
| $ I_{CM} =\displaystyle\frac{1}{12} m ( a ^2+ b ^2)$ |
(ID 4433)
El momento de Inercia CM de una Esfera ($I_{CM}$) se obtiene en función de la masa del cuerpo ($m$) y el radio de esfera ($r_e$):
| $ I_{CM} =\displaystyle\frac{2}{5} m r_e ^2$ |
(ID 4436)
La energía cinética de rotación ($K_r$) es una función de la velocidad angular ($\omega$) y de una medida de la inercia representada por el momento de inercia para eje que no pasa por el CM ($I$):
| $ K_r =\displaystyle\frac{1}{2} I \omega ^2$ |
(ID 3255)
ID:(1417, 0)
