Ley de Gauss
Storyboard 
La ley de Gauss dice que si se tiene una superficie cerrada y se suma la proyección del campo eléctrico sobre toda la superficie es proporcional a la carga contenida en el volumen.
ID:(824, 0)
Ley de Gauss
Storyboard 
La ley de Gauss dice que si se tiene una superficie cerrada y se suma la proyección del campo eléctrico sobre toda la superficie es proporcional a la carga contenida en el volumen.
Variables
Cálculos
Cálculos
Ecuaciones
El campo eléctrico en superficie i ($\vec{E}_i$) y el versor normal a la superficie i ($\hat{n}_i$), multiplicada por la elemento de superficie i ($dS_i$) para cada elemento $i$, que luego se suma sobre toda la secci n, es igual a la carga total ($Q_t$) dividido por la constante de campo eléctrico ($\epsilon_0$) y la constante dieléctrica ($\epsilon$):
Con el elemento de superficie ($dS$) del producto punto de el campo eléctrico ($\vec{E}$) y el versor normal a la sección ($\hat{n}$), se obtiene la versi n continua de la ley de Gauss:
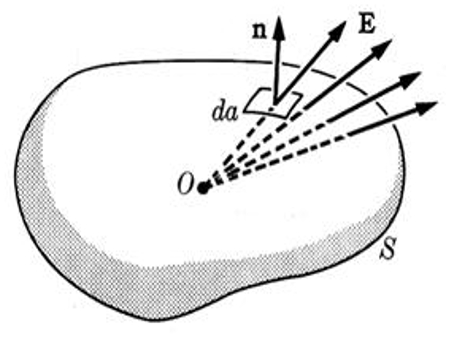
El flujo eléctrico ($\Phi$) se define como la componente normal del campo el ctrico, calculada a partir de el campo eléctrico en superficie i ($\vec{E}_i$) y el versor normal a la superficie i ($\hat{n}_i$), multiplicada por la elemento de superficie i ($dS_i$) para cada elemento
i, que luego se suma sobre toda la secci n:
La magnitud de el campo eléctrico ($E$) generada por la carga ($Q$), que se encuentran a una distancia de la distancia ($r$), se calcula utilizando la constante de campo eléctrico ($\epsilon_0$) y la constante dieléctrica ($\epsilon$) de la siguiente manera:
Dado que la superficie de una esfera ($S$) es con la distancia ($r$):
Se tiene que el flujo es:
$\Phi = | \vec{E} | S = \displaystyle\frac{1}{4 \pi \epsilon \epsilon_0} \displaystyle\frac{ Q }{ r ^2} 4 \pi r ^2=\displaystyle\frac{ Q }{ \epsilon_0 \epsilon }$
Con lo que se puede inferir que la relaci n es:
Ejemplos
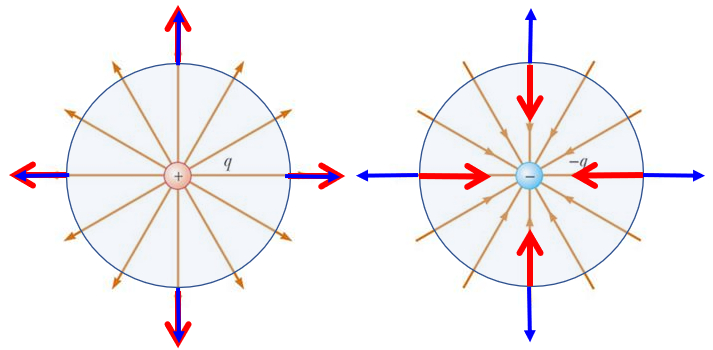
Si la superficie rodea una carga se observa que no existe compensaci n y que el flujo solo depende del signo de la carga:
• si la carga es positiva, los versores normales son paralelos al campo y el flujo resulta positivo
• si la carga es negativa los versores normales son anti paralelos al campo y el flujo resulta negativo
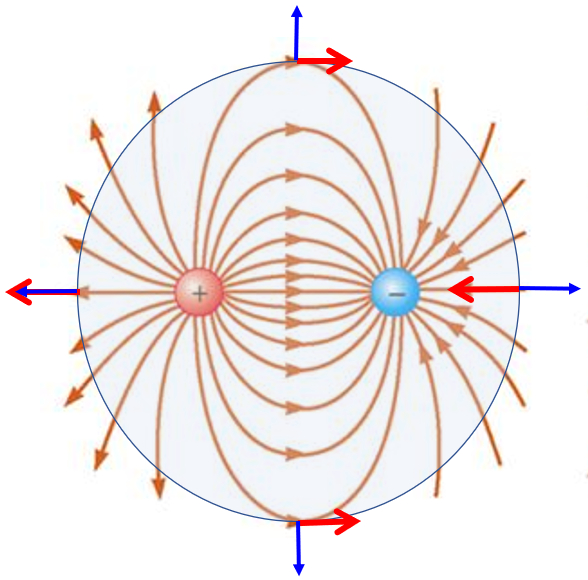
Si se consideran dos cargas opuestas y se estudia el flujo a trav s de una superficie que contiene a ambas, observamos que los flujos nuevamente se compensan siendo al final el flujo total nulo. De esta forma concluimos que:
• no existe flujo total en un volumen que no contiene cargas
• no existe flujo total en un volumen que contiene un igual numero de cargas positivas y negativas
• solo existe flujo total en la medida que existan cargas cuya suma total no sea nula
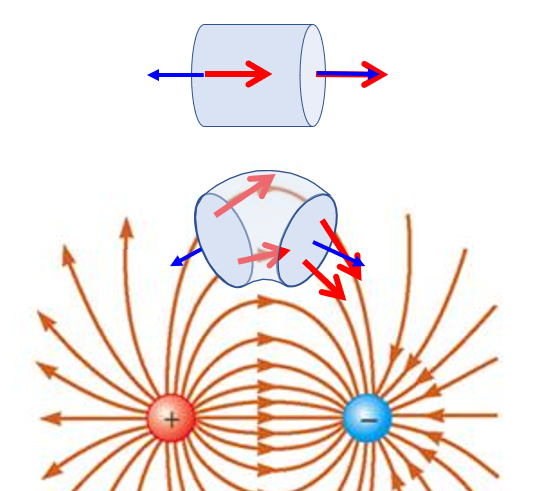
Si se toma un elemento de volumen y se le coloca en un flujo el ctrico se observara que un lado del cuerpo esta orientado a lo largo del campo mientras el lado opuesto esta orientado en el sentido opuesto al campo:
Esto lleva a que el flujo que 'sale' se compense con el que 'entra'. Esto es solo si no hay cargas al interior o sea que no existe una fuente o sumidero que genere o destruya lineas de campo. En ese sentido se puede hablar de la conservaci n del flujo igual que en un liquido.
El flujo eléctrico ($\Phi$) se define como la componente normal del campo el ctrico, calculada a partir de el campo eléctrico en superficie i ($\vec{E}_i$) y el versor normal a la superficie i ($\hat{n}_i$), multiplicada por la elemento de superficie i ($dS_i$) para cada elemento
i, que luego se suma sobre toda la secci n:
La magnitud de el campo eléctrico ($E$) generada por la carga ($Q$), que se encuentran a una distancia de la distancia ($r$), se calcula utilizando la constante de campo eléctrico ($\epsilon_0$) y la constante dieléctrica ($\epsilon$) de la siguiente manera:
Dado que la superficie de una esfera ($S$) es con la distancia ($r$):
Se tiene que el flujo es:
$\Phi = | \vec{E} | S = \displaystyle\frac{1}{4 \pi \epsilon \epsilon_0} \displaystyle\frac{ Q }{ r ^2} 4 \pi r ^2=\displaystyle\frac{ Q }{ \epsilon_0 \epsilon }$
Con lo que se puede inferir que la relaci n es:
Con el elemento de superficie ($dS$) del producto punto de el campo eléctrico ($\vec{E}$) y el versor normal a la sección ($\hat{n}$), se obtiene la versi n continua de la ley de Gauss:
Esta corresponde a la versi n de la ecuaci n de Gauss descubierta en 1835 que se publico en forma postuma [1].
![]() [1] "Allgemeine Lehrs tze in Beziehung auf die im verkehrten Verh ltnisse des Quadrats der Entfernung wirkenden Anziehungs- und Abstossungskr fte" (Teoremas generales relacionados con las fuerzas de atracci n y repulsi n que act an en la proporci n invertida del cuadrado de la distancia), Carl Friedrich Gauss, Werke, 1867
[1] "Allgemeine Lehrs tze in Beziehung auf die im verkehrten Verh ltnisse des Quadrats der Entfernung wirkenden Anziehungs- und Abstossungskr fte" (Teoremas generales relacionados con las fuerzas de atracci n y repulsi n que act an en la proporci n invertida del cuadrado de la distancia), Carl Friedrich Gauss, Werke, 1867
La ley de Gauss considera las l neas de campo respecto a una superficie cerrada.
• Si la superficie no encierra ninguna carga, las l neas de campo se conservan, es decir, fluyen tanto hacia adentro como hacia afuera de la superficie.
• Si la superficie rodea una carga la carga total ($Q_t$), se crean (carga positiva) o se destruyen (carga negativa) un n mero proporcional a dicha carga.
• Si las cargas contenidas en su suma son nulas, la suma de las componentes del campo perpendiculares a la superficie tambi n ser nula.
En el interior de un conductor se puede definir una superficie
por ello el campo el ctrico es nulo. El conductor genera lo que se llama una jaula de Faraday.
El fuselaje de un avi n de pasajeros es generalmente un buen conductor de electricidad. Por ello, si un avi n es impactado por un rayo, las cargas se distribuyen sobre su superficie y, por la ley de Gauss, no se genera un campo el ctrico en el interior de la aeronave.
De esta manera, los pasajeros no sufren da o y, finalmente, la carga contin a su camino, generando un nuevo rayo que se desplaza hacia alg n otro lugar cargado positivamente.
Por ello, se asume que los rayos no son peligrosos para los aviones en vuelo y que cada avi n sufre varios impactos al a o. Sin embargo, existe un riesgo durante el proceso de aterrizaje: si el avi n es tocado por un rayo en el momento de posarse en tierra, las cargas pueden fluir por los neum ticos hacia la pista, generando niveles de calor que pueden da arlos. En general, los pilotos est n entrenados para manejar situaciones en las que el tren de aterrizaje sufre da os, por lo que el riesgo para los pasajeros no es tan elevado. Sin embargo, el da o a la aeronave puede ser mayor y requerir una reparaci n m s extensa antes de poder volver a operar.
El flujo depende de la carga total ($Q_t$) contenida en el volumen que las contiene. Por ello, debemos sumar todas las la carga i ($q_i$) contenidas, independientemente de su posici n:
El campo eléctrico en superficie i ($\vec{E}_i$) y el versor normal a la superficie i ($\hat{n}_i$), multiplicadas por la elemento de superficie i ($dS_i$) para cada elemento $i$, y luego sumadas sobre toda la secci n, son iguales a la carga total ($Q_t$) dividido por la constante de campo eléctrico ($\epsilon_0$) y la constante dieléctrica ($\epsilon$):
Con el elemento de superficie ($dS$) del producto punto de el campo eléctrico ($\vec{E}$) y el versor normal a la sección ($\hat{n}$), y la carga total ($Q_t$) dividido por la constante de campo eléctrico ($\epsilon_0$) y la constante dieléctrica ($\epsilon$), se llega a la expresi n de la ley de Gauss:
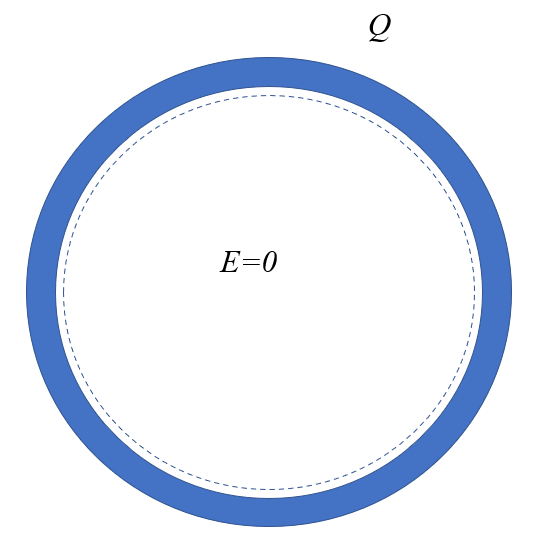
Consideremos una esfera hueca con cargas distribuidas uniformemente en su superficie. En este caso, podemos definir una superficie interna dentro de la esfera. Como la cantidad de carga la carga total ($Q_t$) contenida en el volumen encerrado por esta superficie interna es cero, el campo el ctrico el campo eléctrico ($E$) tambi n ser cero:
ID:(824, 0)