mechanisms

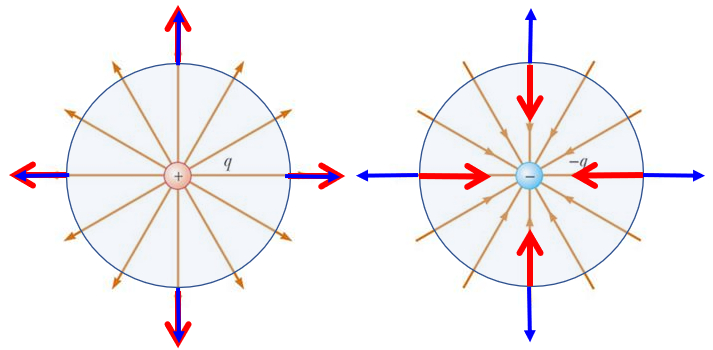
Wenn die Oberfl che eine Last umgibt, wird festgestellt, dass es keine Kompensation gibt und dass der Durchfluss nur vom Vorzeichen der Last abh ngt:

• Wenn die Ladung positiv ist, sind die normalen Verse parallel zum Feld und der Fluss ist positiv

• Wenn die Ladung negativ ist, sind die normalen Verse antiparallel zum Feld und der Fluss ist negativ

image

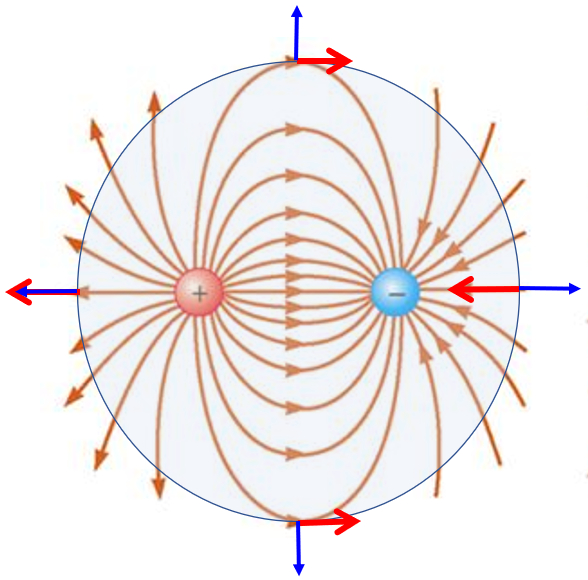
Wenn wir zwei entgegengesetzte Ladungen betrachten und den Fluss durch eine Oberfl che untersuchen, die beide enth lt, stellen wir fest, dass die Fl sse wieder kompensiert werden und am Ende der Gesamtfluss Null sind. Auf diese Weise schlie en wir, dass:

• In einem Volumen, das keine Ladungen enth lt, ist kein vollst ndiger Durchfluss vorhanden

• Es gibt keinen Gesamtfluss in einem Volumen, das die gleiche Anzahl positiver und negativer Ladungen enth lt

• Es gibt nur dann einen Gesamtdurchfluss, wenn es Lasten gibt, deren Gesamtsumme nicht Null ist

image

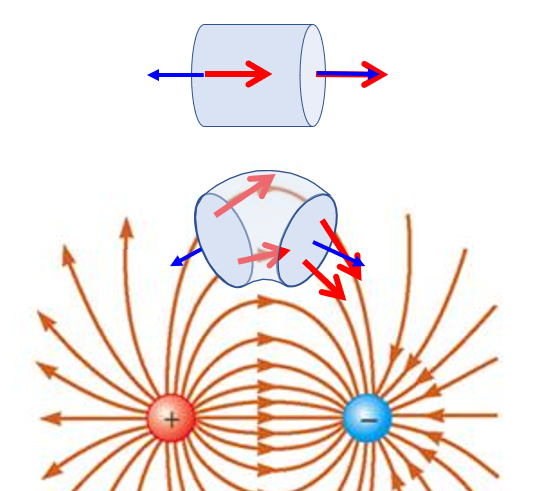
Wenn ein Volumenelement genommen und in einen elektrischen Fluss gebracht wird, wird beobachtet, dass eine Seite des K rpers entlang des Feldes ausgerichtet ist, w hrend die gegen berliegende Seite in die entgegengesetzte Richtung zum Feld ausgerichtet ist:

image

Dies f hrt dazu, dass der Fluss, der 'ausgeht', f r den Fluss, der 'eintritt', kompensiert wird. Dies ist nur dann der Fall, wenn keine Ladungen im Inneren vorhanden sind, dh wenn keine Quelle oder Senke vorhanden ist, die Feldlinien erzeugt oder zerst rt. In diesem Sinne kann man von der Erhaltung der Str mung wie in einer Fl ssigkeit sprechen.

Der Elektrischer Fluss ($\Phi$) wird als die Normalkomponente des elektrischen Feldes definiert, berechnet aus der Elektrisches Oberflächenfeld i ($\vec{E}_i$) und der Versor normal zur Oberfläche i ($\hat{n}_i$), multipliziert mit die Oberflächenelement i ($dS_i$) f r jedes Element

i, das dann ber die gesamte Fl che summiert wird:

equation=11372

Die Gr e von der Elektrisches Feld ($E$), die durch die Ladung ($Q$) erzeugt wird und sich in einem Abstand von die Entfernung ($r$) befindet, wird wie folgt unter Verwendung von die Elektrische Feldkonstante ($\epsilon_0$) und die Dielektrizitätskonstante ($\epsilon$) berechnet:

equation=11379

Da die Oberfläche einer Kugel ($S$) mit die Entfernung ($r$) ist:

equation=4731

Der Fluss ist:

$\Phi = | \vec{E} | S = \displaystyle\frac{1}{4 \pi \epsilon \epsilon_0} \displaystyle\frac{ Q }{ r ^2} 4 \pi r ^2=\displaystyle\frac{ Q }{ \epsilon_0 \epsilon }$

Daraus l sst sich ableiten, dass die Beziehung ist:

equation=11377

Unter Verwendung von der Oberflächenelement ($dS$) f r das Skalarprodukt von der Elektrisches Feld ($\vec{E}$) und der Versor normal zum Abschnitt ($\hat{n}$) erhalten wir die kontinuierliche Version des Gau schen Gesetzes:

equation=3213

Dies entspricht der Version der Gau schen Gleichung, die 1835 entdeckt und posthum ver ffentlicht wurde [1].

[1] 'Allgemeine Lehrs tze in Beziehung auf die im verkehrten Verh ltnisse des Quadrats der Entfernung wirkenden Anziehungs- und Abstossungskr fte' (Allgemeine Lehrs tze bez glich der Kr fte der Anziehung und Absto ung, die im Verh ltnis zum Quadrat der Entfernung wirken), Carl Friedrich Gauss, Werke, 1867

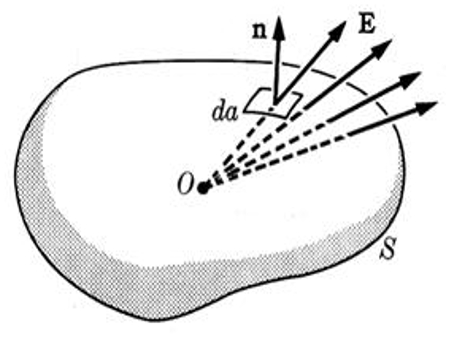
Das Gau sche Gesetz betrachtet die Feldlinien in Bezug auf eine geschlossene Oberfl che.

• Wenn die Oberfl che keine Ladung einschlie t, bleiben die Feldlinien erhalten, das hei t, sie flie en sowohl in die Oberfl che hinein als auch aus der Oberfl che heraus.

• Wenn die Oberfl che eine Ladung die Gesamtbeladung ($Q_t$) einschlie t, wird eine Anzahl proportional zu dieser Ladung entweder erzeugt (positive Ladung) oder vernichtet (negative Ladung).

• Wenn die Summe der eingeschlossenen Ladungen null ist, ist auch die Summe der senkrechten Komponenten des Feldes zur Oberfl che null.

image

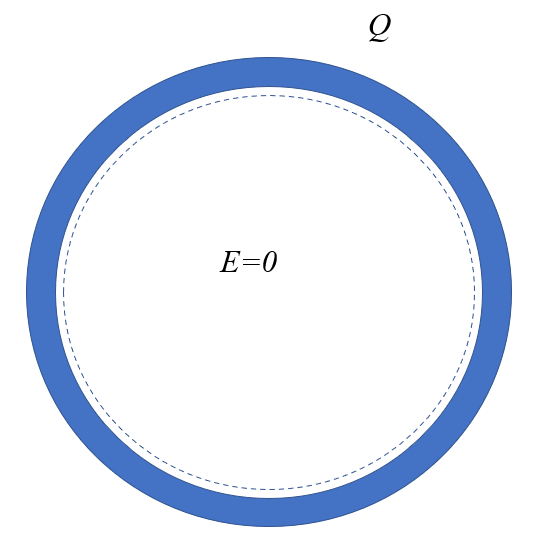
Innerhalb eines Leiters k nnen Sie eine Oberfl che S definieren, die ein leeres Volumen einschlie t, in dem keine Last vorhanden ist Q=0:

image

daher ist das elektrische Feld null. Der Fahrer erzeugt einen sogenannten Faradayschen K fig.

Der Rumpf eines Passagierflugzeugs ist in der Regel ein guter Leiter. Daher verteilen sich die Ladungen bei einem Blitzschlag ber die Oberfl che des Flugzeugs und es entsteht gem dem Gau schen Gesetz kein elektrisches Feld im Inneren des Flugzeugs.

equation=3842

Auf diese Weise erleiden die Passagiere keinen Schaden und schlie lich setzt die Ladung ihren Weg fort, indem sie einen neuen Blitz erzeugt, der sich zu einem anderen positiv geladenen Ort bewegt.

image

Daher gelten Blitze nicht als gef hrlich f r Flugzeuge im Flug und jedes Flugzeug wird mehrere Male pro Jahr getroffen. Es besteht jedoch ein Risiko w hrend des Landevorgangs: Wenn das Flugzeug im Moment der Landung von einem Blitz getroffen wird, k nnen die Ladungen durch die Reifen zur Landebahn flie en, wodurch Hitze entsteht, die diese besch digen kann. Piloten sind im Allgemeinen darauf trainiert, Situationen zu bew ltigen, in denen das Fahrwerk besch digt wird, sodass das Risiko f r die Passagiere nicht sehr hoch ist. Der Schaden am Flugzeug kann jedoch erheblich sein und umfangreiche Reparaturen erfordern, bevor es wieder in Betrieb genommen werden kann.

model

Der Fluss h ngt von die Gesamtbeladung ($Q_t$) ab, die im Volumen enthalten sind. Daher m ssen wir alle enthaltenen die Ladung i ($q_i$) summieren, unabh ngig von ihrer Position:

kyon

Der Elektrisches Oberflächenfeld i ($\vec{E}_i$) und der Versor normal zur Oberfläche i ($\hat{n}_i$), multipliziert mit die Oberflächenelement i ($dS_i$) f r jedes Element $i$, und dann ber die gesamte Fl che summiert, sind gleich die Gesamtbeladung ($Q_t$) dividiert durch die Elektrische Feldkonstante ($\epsilon_0$) und die Dielektrizitätskonstante ($\epsilon$):

kyon

Unter Verwendung von der Oberflächenelement ($dS$) f r das Skalarprodukt von der Elektrisches Feld ($\vec{E}$) und der Versor normal zum Abschnitt ($\hat{n}$) und die Gesamtbeladung ($Q_t$) geteilt durch die Elektrische Feldkonstante ($\epsilon_0$) und die Dielektrizitätskonstante ($\epsilon$) gelangen wir zur Ausdruck der Gau schen Gesetz:

kyon

Betrachten wir eine hohle Ladung, d.h. eine hohle Kugel mit Ladungen auf ihrer Oberfl che. In diesem Fall k nnen wir eine innere Fl che innerhalb der Kugel definieren. Da die Menge der Ladung die Gesamtbeladung ($Q_t$), die im Volumen enthalten ist, null ist, wird auch das elektrische Feld der Elektrisches Feld ($E$) null sein:

kyon