Usuario:
Flujo de Gases
Storyboard 
Con la presión se genera el flujo que en el caso que se considere la viscosidad del medio afecta la velocidad con que el gas se desplaza. Dicha dependencia depende en particular del radio del canal como del largo de este.
ID:(731, 0)
Flujo de Gases
Descripción
Con la presión se genera el flujo que en el caso que se considere la viscosidad del medio afecta la velocidad con que el gas se desplaza. Dicha dependencia depende en particular del radio del canal como del largo de este.
Variables
Cálculos
a 
,
luego, seleccione la variable: 
a 
Cálculos
Variable
Dado
Calcule
Objetivo :
Ecuación
A utilizar
Ecuaciones
(ID 939)
Si consideramos el perfil de ERROR:5449,0 de un fluido en un canal cil ndrico, donde la velocidad en un radio del cilindro ($v$) var a en funci n de ERROR:10120,0 de acuerdo con la siguiente expresi n:
| $ v = v_{max} \left(1-\displaystyle\frac{ r ^2}{ R ^2}\right)$ |
con el radio del tubo ($R$) y la velocidad máxima del flujo ($v_{max}$). Podemos calcular la velocidad máxima del flujo ($v_{max}$) utilizando la viscosidad ($\eta$), la diferencia de presión ($\Delta p$) y el largo de tubo ($\Delta L$) de la siguiente manera:
| $ v_{max} =-\displaystyle\frac{ R ^2}{4 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
Si integramos la velocidad en toda la secci n transversal del canal, obtendremos el flujo de volumen ($J_V$), definida como la integral de $\pi r v(r)$ con respecto a ERROR:10120,0 desde $0$ hasta ERROR:5417,0. Esta integral se simplifica de la siguiente manera:
$J_V=-\displaystyle\int_0^Rdr \pi r v(r)=-\displaystyle\frac{R^2}{4\eta}\displaystyle\frac{\Delta p}{\Delta L}\displaystyle\int_0^Rdr \pi r \left(1-\displaystyle\frac{r^2}{R^2}\right)$
La integraci n nos lleva a la ley de Hagen-Poiseuille resultante:
| $ J_V =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
(ID 3178)
El flujo de volumen ($J_V$) se puede determinar a partir de la conductancia hidráulica ($G_h$) y la diferencia de presión ($\Delta p$) utilizando la ecuaci n siguiente:
| $ J_V = G_h \Delta p $ |
Adem s, utilizando la relaci n para la resistencia hidráulica ($R_h$):
| $ R_h = \displaystyle\frac{1}{ G_h }$ |
se obtiene el resultado final:
| $ \Delta p = R_h J_V $ |
(ID 3179)
Una forma de modelar un tubo en el que var a la secci n es dividirlo en secciones de radio constante y luego sumar las resistencias hidr ulicas en serie. Supongamos que tenemos una serie de la resistencia hidráulica en una red ($R_{hk}$), que depende de la viscosidad ($\eta$), el radio del cilindro k ($R_k$) y el largo de tubo k ($\Delta L_k$) a trav s de la siguiente ecuaci n:
| $ R_h =\displaystyle\frac{8 \eta | \Delta L | }{ \pi R ^4}$ |
En cada elemento habr una diferencia de presión en una red ($\Delta p_k$) con la resistencia hidráulica en una red ($R_{hk}$) y el flujo de volumen ($J_V$) para los que se aplica la ley de Darcy
| $ \Delta p = R_h J_V $ |
la diferencia de presión total ($\Delta p_t$) ser igual a la suma de las ERROR:10132,0 individuales
| $ \Delta p_t =\displaystyle\sum_k \Delta p_k $ |
por lo que
$\Delta p_t=\displaystyle\sum_k \Delta p_k=\displaystyle\sum_k (R_{hk}J_V)=\left(\displaystyle\sum_k R_{hk}\right)J_V\equiv R_{st}J_V$
Por lo tanto, el sistema se puede modelar como un conducto nico con la resistencia hidr ulica calculada como la suma de las componentes individuales:
| $ R_{st} =\displaystyle\sum_k R_{hk} $ |
(ID 3180)
La conductancia hidráulica total en paralelo ($G_{pt}$) junto con la conductancia hidráulica en una red ($G_{hk}$) en
| $ G_{pt} =\displaystyle\sum_k G_{hk} $ |
y junto con la resistencia hidráulica en una red ($R_{hk}$) y la ecuaci n
| $ R_h = \displaystyle\frac{1}{ G_h }$ |
conduce a la resistencia hidráulica total en paralelo ($R_{pt}$) mediante
| $\displaystyle\frac{1}{ R_{pt} }=\sum_k\displaystyle\frac{1}{ R_{hk} }$ |
(ID 3181)
(ID 3469)
(ID 3624)
Dado que la resistencia hidráulica ($R_h$) es igual a la conductancia hidráulica ($G_h$) seg n la siguiente ecuaci n:
| $ R_h = \displaystyle\frac{1}{ G_h }$ |
y dado que la conductancia hidráulica ($G_h$) se expresa en t rminos de la viscosidad ($\eta$), el radio del tubo ($R$) y el largo de tubo ($\Delta L$) de la siguiente manera:
| $ G_h =\displaystyle\frac{ \pi R ^4}{8 \eta | \Delta L | }$ |
podemos concluir que:
| $ R_h =\displaystyle\frac{8 \eta | \Delta L | }{ \pi R ^4}$ |
(ID 3629)
(ID 3632)
(ID 4257)
(ID 4502)
(ID 4833)
(ID 4834)
Ejemplos
Si uno observa un tubo de radio
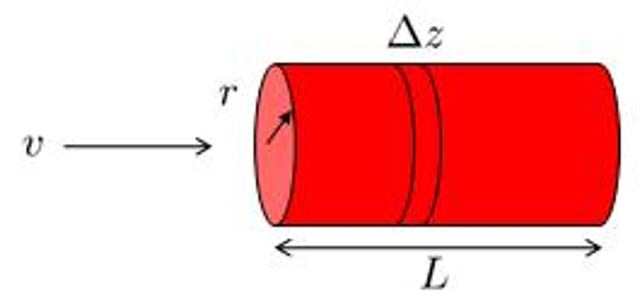
Elemento desplaz ndose por un tubo
(ID 7019)
Un cambio de secci n se puede representar por dos tubos de radio
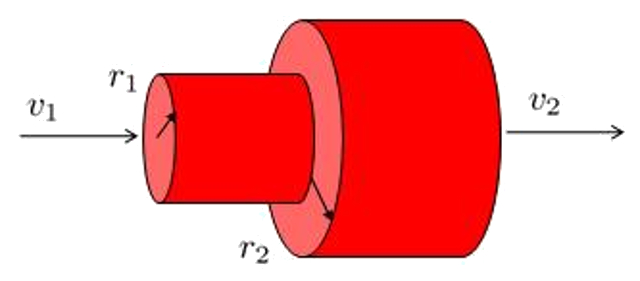
Cambio de secci n
lo que lleva a que la velocidad inicial
(ID 7020)
Para mostrar como el elemento de volumen es empujado por un tubo debemos considerar una fuerza
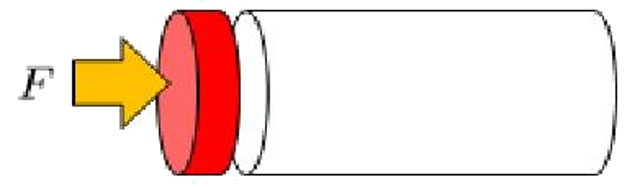
Fuerza sobre un volumen de liquido o gas
(ID 7023)
El elemento en el tubo esta expuesto a las presiones de ambos extremos:
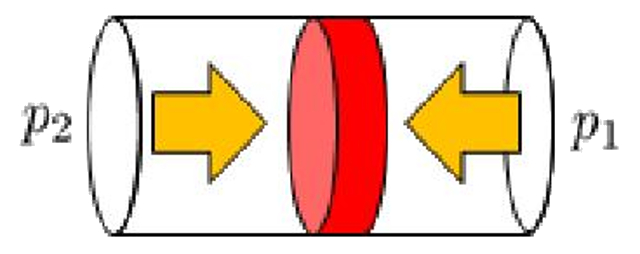
Presiones sobre un elemento de volumen
de modo que se desplaza seg n cualquiera de las dos presiones supere a la otra en direcci n de la menor presi n.
(ID 7024)
ID:(731, 0)