Mittlere Fließgeschwindigkeit im Zylindrischem Kanal
Definition 
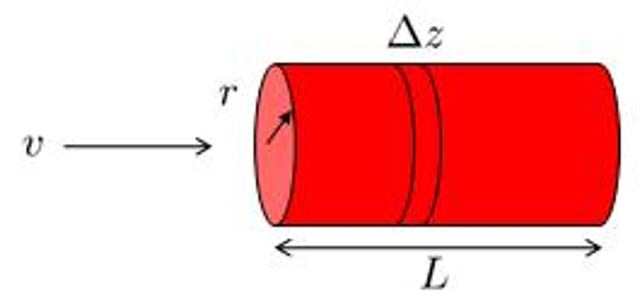
Wenn man ein Rohr mit einem
ID:(7019, 0)
Querschnittsänderung
Bild 
Eine Abschnittsänderung kann durch zwei Funkröhren
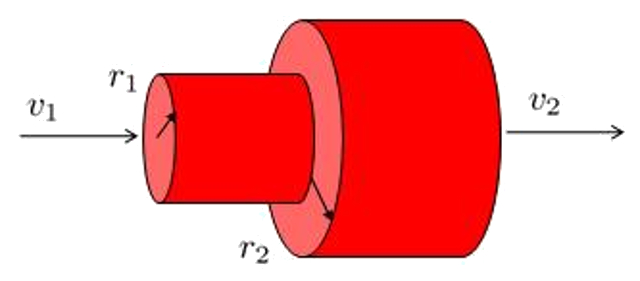
Dies führt dazu, dass die Anfangsgeschwindigkeit
ID:(7020, 0)
Kraft auf ein Flusselement
Notiz 
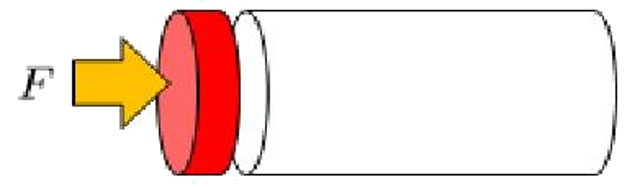
Um zu zeigen, wie das Volumenelement von einem Rohr gedrückt wird, müssen wir eine Kraft
ID:(7023, 0)
Druck auf ein Element des Flusses
Zitat 
Das Element im Rohr ist den Drücken beider Enden ausgesetzt:
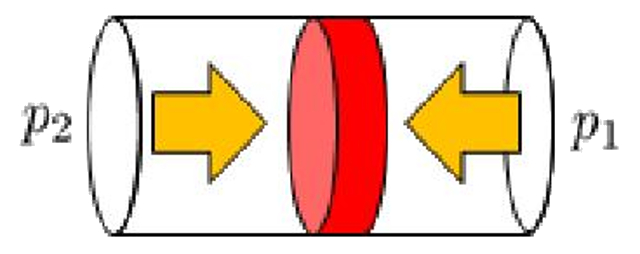
so dass es sich nach einem der beiden Drücke bewegt, der den anderen in Richtung des niedrigsten Drucks übersteigt.
ID:(7024, 0)
Movimeinto de Gases
Storyboard 
Variablen
Berechnungen
Berechnungen
Gleichungen
Wenn wir das Profil von ERROR:5449,0 f r ein Fluid in einem zylindrischen Kanal betrachten, in dem die Geschwindigkeit auf einer Zylinder-Radio ($v$) in Abh ngigkeit von ERROR:10120,0 gem folgendem Ausdruck variiert:
unter Verwendung von der Rohrradius ($R$) und die Maximale Durchflussrate ($v_{max}$). K nnen wir die Maximale Durchflussrate ($v_{max}$) mithilfe von die Viskosität ($\eta$), die Druckunterschied ($\Delta p$) und der Rohrlänge ($\Delta L$) wie folgt berechnen:
Wenn wir die Geschwindigkeit ber den Querschnitt des Kanals integrieren, erhalten wir der Volumenstrom ($J_V$), definiert als das Integral von $\pi r v(r)$ bez glich ERROR:10120,0 von $0$ bis ERROR:5417,0. Dieses Integral kann wie folgt vereinfacht werden:
$J_V=-\displaystyle\int_0^Rdr \pi r v(r)=-\displaystyle\frac{R^2}{4\eta}\displaystyle\frac{\Delta p}{\Delta L}\displaystyle\int_0^Rdr \pi r \left(1-\displaystyle\frac{r^2}{R^2}\right)$
Die Integration f hrt zur resultierenden Hagen-Poiseuille-Gesetz:
Der Volumenstrom ($J_V$) kann aus die Hydraulische Leitfähigkeit ($G_h$) und die Druckunterschied ($\Delta p$) unter Verwendung der folgenden Gleichung berechnet werden:
Weiterhin, unter Verwendung der Beziehung f r die Hydraulic Resistance ($R_h$):
ergibt sich:
Eine M glichkeit, ein Rohr mit variierendem Querschnitt zu modellieren, besteht darin, es in Abschnitte mit konstantem Radius zu unterteilen und dann die hydraulischen Widerst nde in Serie zu addieren. Nehmen wir an, wir haben eine Serie von die Hydraulischer Widerstand in einem Netzwerk ($R_{hk}$), die abh ngig von die Viskosität ($\eta$), der Zylinder k Radio ($R_k$) und der Länge des Rohrs k ($\Delta L_k$) durch die folgende Gleichung bestimmt wird:
In jedem Segment gibt es eine Druckunterschied in einem Netzwerk ($\Delta p_k$) mit die Hydraulischer Widerstand in einem Netzwerk ($R_{hk}$) und der Volumenstrom ($J_V$), auf die das Darcysche Gesetz angewendet wird:
die Gesamtdruckdifferenz ($\Delta p_t$) wird gleich der Summe der einzelnen ERROR:10132,0 sein:
daher,
$\Delta p_t=\displaystyle\sum_k \Delta p_k=\displaystyle\sum_k (R_{hk}J_V)=\left(\displaystyle\sum_k R_{hk}\right)J_V\equiv R_{st}J_V$
Somit kann das System als ein einzelner Leiter modelliert werden, dessen hydraulischer Widerstand als Summe der einzelnen Komponenten berechnet wird:
Die Parallele hydraulische Gesamtleitfähigkeit ($G_{pt}$) in Kombination mit die Hydraulische Leitfähigkeit in einem Netzwerk ($G_{hk}$) in
und zusammen mit die Hydraulischer Widerstand in einem Netzwerk ($R_{hk}$) und der Gleichung
f hrt zu die Insgesamt hydraulischen Widerstand in Parallel ($R_{pt}$) ber
Da die Hydraulic Resistance ($R_h$) gem der folgenden Gleichung gleich die Hydraulische Leitfähigkeit ($G_h$) ist:
und da die Hydraulische Leitfähigkeit ($G_h$) wie folgt in Bezug auf die Viskosität ($\eta$), der Rohrradius ($R$) und der Rohrlänge ($\Delta L$) ausgedr ckt wird:
k nnen wir folgern, dass:
Beispiele
Die Volumen nderung zwischen $V_1$ und $V_2$ wird wie folgt dargestellt:
Die Zeit zwischen
Der Volumenstrom ($J_V$) entspricht der Volume Fließende ($\Delta V$), das durch den Kanal bei der Abgelaufene Zeit ($\Delta t$) flie t. Daher haben wir:
Wenn man ein Rohr mit einem
Wenn wir ein Rohr mit einer die Rohr Sektion ($S$) haben, das eine Strecke von der Rohrelement ($\Delta s$) entlang seiner Achse bewegt hat, nachdem es der Volumenelement ($\Delta V$) verschoben wurde, dann ist es gleich:
Mit der Flussdefinition
und das des Volumenelements
kann mit der Definition der Geschwindigkeit erhalten werden
dass die Str mungsdichte gleich der Durchschnittsgeschwindigkeit ist:
Wenn Sie einen Gesamtfluss
Eine der grundlegendsten Gesetze in der Physik ist die Erhaltung der Masse, die in unserer makroskopischen Welt gilt. Nur in der mikroskopischen Welt existiert eine Umwandlung zwischen Masse und Energie, die wir in diesem Fall nicht ber cksichtigen werden. Im Falle eines Fluids bedeutet dies, dass die Masse, die durch ein Rohr eintritt, gleich der Masse sein muss, die es verl sst.
Wenn die Dichte konstant ist, gilt dasselbe f r das Volumen. In solchen F llen, wenn wir den Fluss als ein inkompressibles Fluid behandeln, bedeutet dies, dass ein bestimmtes Volumen, das an einem Ende des Rohrs eintritt, am anderen Ende austreten muss. Dies kann als Gleichheit zwischen der Fließen in Position 1 ($J_1$) und der Fließen in Position 2 ($J_2$) ausgedr ckt werden, mit der Gleichung:
Wenn wir annehmen, dass die Fl ssigkeit inkompressibel ist, das hei t, sie kann nicht komprimiert werden, wird ihr Volumen immer gleich bleiben. In diesem Fall besagt die Kontinuit t, dass das Volumen, das in ein Rohr eintritt, dem Volumen entsprechen muss, das es verl sst. Das bedeutet, dass die anf ngliche Flussrate, gekennzeichnet als $J_1$, und die endg ltige Flussrate, gekennzeichnet als $J_2$, gleich sein m ssen.
Eine Abschnitts nderung kann durch zwei Funkr hren
Dies f hrt dazu, dass die Anfangsgeschwindigkeit
Um zu zeigen, wie das Volumenelement von einem Rohr gedr ckt wird, m ssen wir eine Kraft
Das Element im Rohr ist den Dr cken beider Enden ausgesetzt:
so dass es sich nach einem der beiden Dr cke bewegt, der den anderen in Richtung des niedrigsten Drucks bersteigt.
Der Volumenstrom ($J_V$) l sst sich mit dem Hagen-Poiseuille-Gesetz berechnen, das mit den Parametern die Viskosität ($\eta$), die Druckunterschied ($\Delta p$), der Rohrradius ($R$) und der Rohrlänge ($\Delta L$) lautet:
Darcy schreibt die Hagen-Poiseuille-Gleichung so um, dass die Druckunterschied ($\Delta p$) gleich die Hydraulic Resistance ($R_h$) mal der Volumenstrom ($J_V$) ist:
Da die Hydraulic Resistance ($R_h$) dem Kehrwert von die Hydraulische Leitfähigkeit ($G_h$) entspricht, kann es aus dem Ausdruck des letzteren berechnet werden. Auf diese Weise k nnen wir Parameter identifizieren, die mit der Geometrie (der Rohrlänge ($\Delta L$) und der Rohrradius ($R$)) und der Art des Fluids (die Viskosität ($\eta$)) zusammenh ngen und die gemeinsam als eine Hydraulic Resistance ($R_h$) bezeichnet werden k nnen:
Wenn mehrere hydraulische Widerst nde in Serie geschaltet sind, k nnen wir die Insgesamt hydraulischen Widerstand in Serie ($R_{st}$) berechnen, indem wir die Hydraulischer Widerstand in einem Netzwerk ($R_{hk}$) summieren, wie in der folgenden Formel ausgedr ckt:
Wenn Sie
Die Insgesamt hydraulischen Widerstand in Parallel ($R_{pt}$) kann als Kehrwert der Summe von die Hydraulischer Widerstand in einem Netzwerk ($R_{hk}$) berechnet werden:
Wenn Sie
ID:(731, 0)
