Modelo del Pulmón
Storyboard 
Con las leyes de los gases tanto para el calculo de la relación presión volumen como para el flujo que genera la presión se puede modelar como el aire entra y sale de nuestros pulmones incluyendo la dinámica de inflar y desinflar los alvéolo.
ID:(730, 0)
Estructura del modelo del pulmón
Definición 
Modelo general de pulmón. Por un lado se tiene el pulmón en si que esta encapsulado por las costillas. En su interior tenemos los conductos y alvéolos.
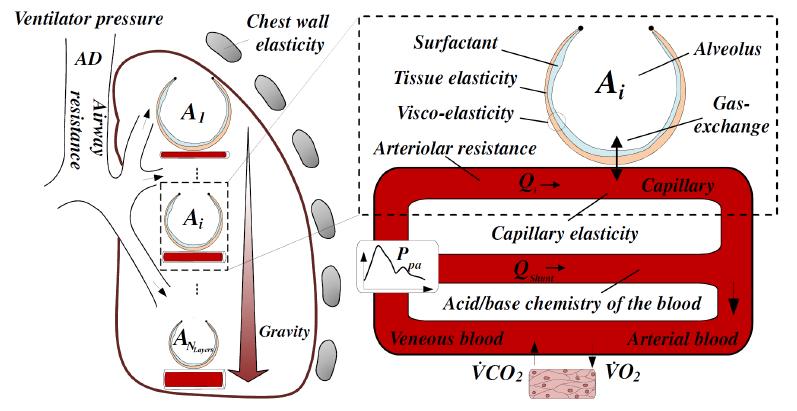
Estructura del modelo del pulmón
ID:(7365, 0)
Estructura del pulmón
Imagen 
La estructura del pulmón se puede describir como una serie de conductos que se van habiendo cada vez en mas conductos de menor radio.
La estructura básica se describe a continuación (pulmón de adulto):
z | n(z) | d(z) [cm] | l(z) [cm]
:-|:-----:|:------------:|:----------:
0 | 1 | 1.8 | 12
1 | 2 | 1.22 | 4.76
2 | 4 | 0.83 | 1.9
3 | 8 | 0.56 | 2.76
4 | 16 | 0.45 | 1.27
5 | 32 | 0.35 | 1.07
6 | 64 | 0.28 | 0.9
7 | 128 | 0.23 | 0.76
8 | 256 | 0.186 | 0.64
9 | 512 | 0.154 | 0.54
10 | 1024 | 0.13 | 0.46
11 | 2048 | 0.109 | 0.39
12 | 4096 | 0.095 | 0.33
13 | 8192 | 0.082 | 0.27
14 | 16384 | 0.074 | 0.23
15 | 32768 | 0.066 | 0.2
16 | 65536 | 0.06 | 0.165
17 | 131072 | 0.054 | 0.141
18 | 262144 | 0.05 | 0.117
19 | 524288 | 0.047 | 0.099
20 | 1048576 | 0.045 | 0.083
21 | 2097152 | 0.043 | 0.07
22 | 4194304 | 0.041 | 0.059
23 | 8388608 | 0.041 | 0.05
ID:(7349, 0)
Volúmenes al respirar
Nota 
El pulmón se puede modelar como dos volumen básicos, el volumen de la traquea y los bronquios que no varia demasiado en el proceso de respiración, y el volumen de los alvéolos que varia.
El volumen de los alvéolo tiene un volumen máximo que se puede estimar asumiendo un radio de
En el caso de que respiramos sin hacer un mayor esfuerzo se habla que aspiramos y exhalamos un volumen del orden de 0.5 litros.
Si hacemos ejercicios, dicho volumen puede ser ampliado en forma dramática llegando a aproximadamente cinco veces, o sea 2.5 litros.
ID:(7622, 0)
Perfil presión volumen exhalación forzada
Cita 
Si se gráfica la relación flujo vs volumen exhalado para el caso de un pulmón normal o otro con alguna deficiencia se obtiene la curva indicada:
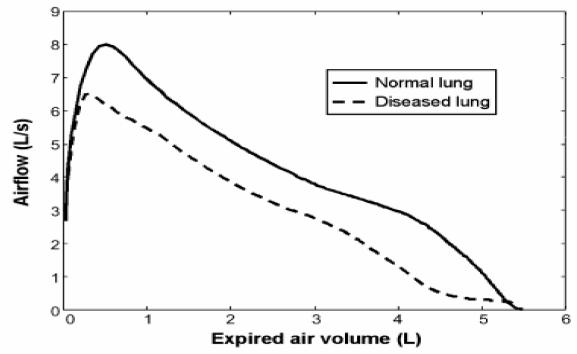
Flujo vs volumen exhalado
Se observa así que el flujo es máximo inicialmente cuando el volumen exhalado es pequeño.
ID:(7362, 0)
Tensión superficial en el tejido del alvéolo
Ejercicio 
La tensión superficial del alvéolo varia con la deformación de la superficie de este:
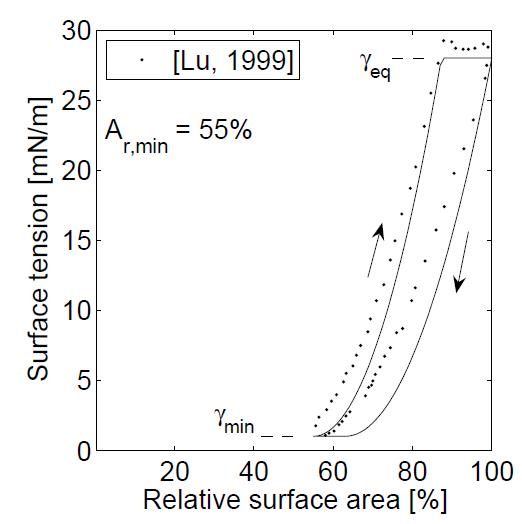
Variación de la tensión superficial
ID:(7368, 0)
Presión de paredes del pulmón
Ecuación 
La presión creada por las paredes del pulmón varían en función del volumen de aire que se inhala en relación a la capacidad del pulmón:
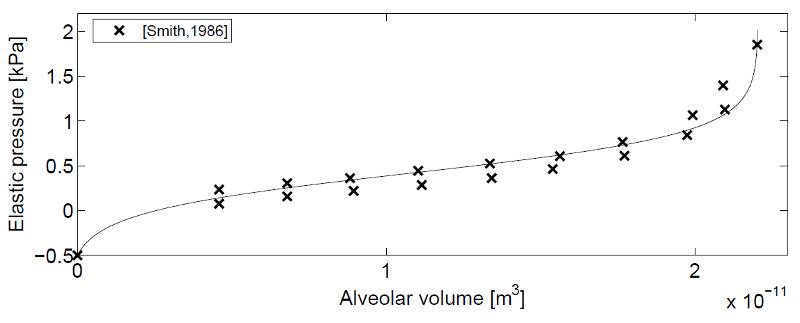
Presión de paredes del pulmón
ID:(7369, 0)
Presión dentro del alvéolo
Script 
La presión dentro del alvéolo es clave para lograr difundir oxigeno a la sangre. Su valor sube con cada inhalación y baja en el proceso de exhalación como indica la curva:
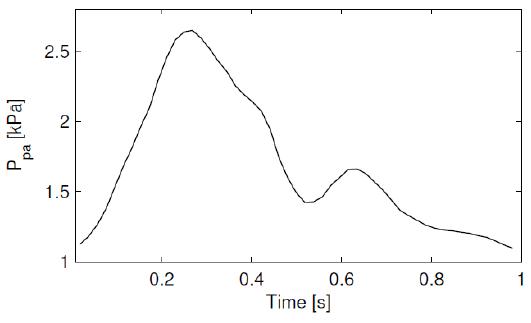
Presión en el alvéolo en función del tiempo
ID:(7367, 0)
Variación del radio del alvéolo con la presión
Variable 
El alvéolo se expande en la medida que la presión sube en su interior:
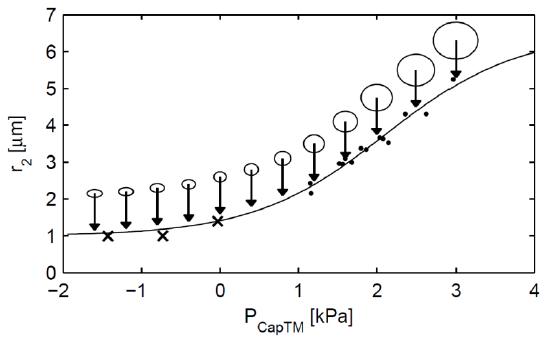
Dilatación de alvéolos por efecto de la presión
ID:(7366, 0)
Modelo dinámico de un pulmón
Audio 
Modelo de oscilación para el estudio dinámico del proceso respiratorio. El árbol mostrado en la imagen corresponde a los alvéolos y como estos se van bifurcando:
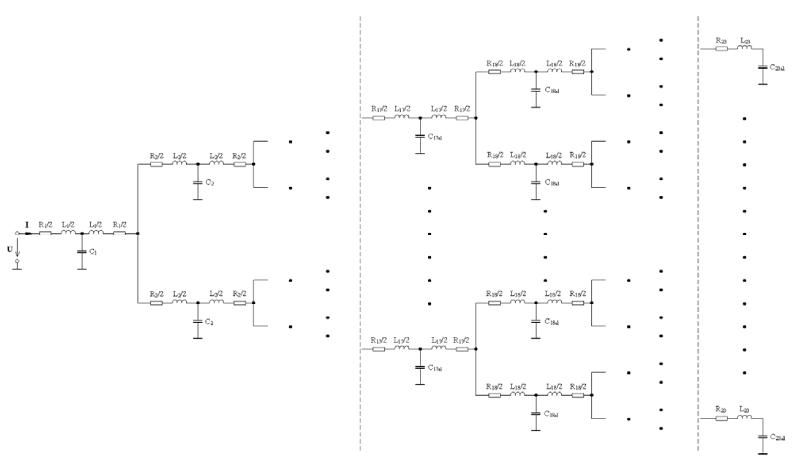
Estructura del pulmón formado por elementos eléctricos que tienen correspondencia con elementos mecánicos.
Cada elemento en el diagrama cuenta con una resistencia, una capacidad y una inductancia permitiendo una oscilación amortiguada.
El modelo tiene especial aplicación en situaciones de uso de ventiladores que generan una respiración forzada.
ID:(7363, 0)
Forma de oscilar bajo respiración forzada
Video 
Diagrama de la oscilación de un modelo dinámico para un pulmón bajo respiración forzada (caso de un adulto). En el se representa la impedancia, que corresponde a una medida de la resistencia, en función de la frecuencia de respiración:
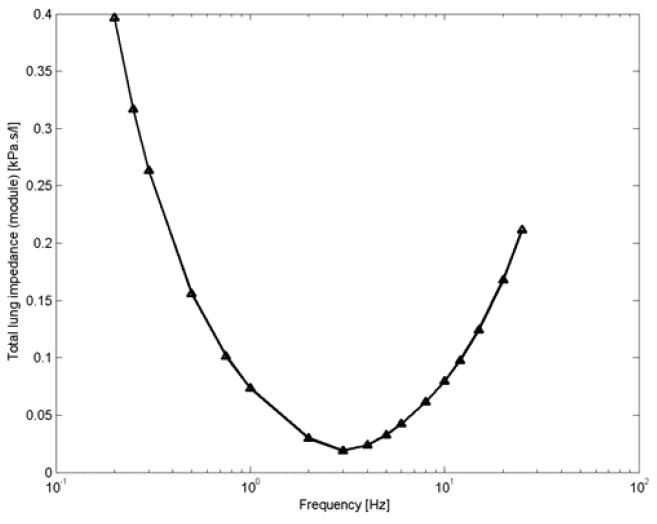
Dependencia de la frecuencia
La curva muestra un mínimo en que el pulmón es capaz de respirar con menor resistencias.
ID:(7364, 0)
Modelo del Pulmón
Storyboard 
Con las leyes de los gases tanto para el calculo de la relación presión volumen como para el flujo que genera la presión se puede modelar como el aire entra y sale de nuestros pulmones incluyendo la dinámica de inflar y desinflar los alvéolo.
Variables
Cálculos
Cálculos
Ecuaciones
Ejemplos
Modelo general de pulm n. Por un lado se tiene el pulm n en si que esta encapsulado por las costillas. En su interior tenemos los conductos y alv olos.
La estructura del pulm n se puede describir como una serie de conductos que se van habiendo cada vez en mas conductos de menor radio.
La estructura b sica se describe a continuaci n (pulm n de adulto):
z | n(z) | d(z) [cm] | l(z) [cm]
:-|:-----:|:------------:|:----------:
0 | 1 | 1.8 | 12
1 | 2 | 1.22 | 4.76
2 | 4 | 0.83 | 1.9
3 | 8 | 0.56 | 2.76
4 | 16 | 0.45 | 1.27
5 | 32 | 0.35 | 1.07
6 | 64 | 0.28 | 0.9
7 | 128 | 0.23 | 0.76
8 | 256 | 0.186 | 0.64
9 | 512 | 0.154 | 0.54
10 | 1024 | 0.13 | 0.46
11 | 2048 | 0.109 | 0.39
12 | 4096 | 0.095 | 0.33
13 | 8192 | 0.082 | 0.27
14 | 16384 | 0.074 | 0.23
15 | 32768 | 0.066 | 0.2
16 | 65536 | 0.06 | 0.165
17 | 131072 | 0.054 | 0.141
18 | 262144 | 0.05 | 0.117
19 | 524288 | 0.047 | 0.099
20 | 1048576 | 0.045 | 0.083
21 | 2097152 | 0.043 | 0.07
22 | 4194304 | 0.041 | 0.059
23 | 8388608 | 0.041 | 0.05
El pulm n se puede modelar como dos volumen b sicos, el volumen de la traquea y los bronquios que no varia demasiado en el proceso de respiraci n, y el volumen de los alv olos que varia.
El volumen de los alv olo tiene un volumen m ximo que se puede estimar asumiendo un radio de
En el caso de que respiramos sin hacer un mayor esfuerzo se habla que aspiramos y exhalamos un volumen del orden de 0.5 litros.
Si hacemos ejercicios, dicho volumen puede ser ampliado en forma dram tica llegando a aproximadamente cinco veces, o sea 2.5 litros.
La superficie de una esfera es con
La superficie total de los alv olos se puede calcular multiplicando la superficie de un alv olo
por el n mero de estos
La tensi n superficial act a en funci n de deformaciones que ocurran a la superficie. Por ello, esta es una funci n del rea actual
Por este motivo se puede introducir una superficie alveolar relativa como
El volumen total de los alv olos se puede calcular multiplicando el volumen de un alv olo
La presi n el stica act a en funci n de deformaciones que ocurran en el volumen. Por ello, esta es una funci n del volumen actual
El volumen m ximo del alv olo se calcula de la capacidad m xima
Si se gr fica la relaci n flujo vs volumen exhalado para el caso de un pulm n normal o otro con alguna deficiencia se obtiene la curva indicada:
Se observa as que el flujo es m ximo inicialmente cuando el volumen exhalado es peque o.
El volumen m ximo que puede exhalar una persona en forma forzada (MEFV) se ha modelado siendo uno de los mejores modelos el de Adam G. Polak de 1998. El modelo da una relaci n entre la presi n y volumen logrado de la forma
donde
Adam G.Polak. A forward model for maximum expiration. Computers in Biology and Medicine 1998; 28: 613-625.
La presi n
La tensi n superficial del alv olo ha sido medida siendo una funci n de la superficie alveolar relativa
donde la constante es
La tensi n superficial del alv olo varia con la deformaci n de la superficie de este:
La presi n de la pared tor cica
donde los factores
La presi n creada por las paredes del pulm n var an en funci n del volumen de aire que se inhala en relaci n a la capacidad del pulm n:
La presi n el stica del alv olo ha sido medida siendo una funci n de volumen relativo
donde las constantes son
La presi n dentro del alv olo es clave para lograr difundir oxigeno a la sangre. Su valor sube con cada inhalaci n y baja en el proceso de exhalaci n como indica la curva:
La presi n en el alv olo
El alv olo se expande en la medida que la presi n sube en su interior:
La pared entre el espacio interior del alv olo y los vasos sangu neos es de solo un micr n facilitando la difusi n de las mol culas de oxigeno y di xido de carb n. El volumen que logra migrar
La constante es del orden de
Modelo de oscilaci n para el estudio din mico del proceso respiratorio. El rbol mostrado en la imagen corresponde a los alv olos y como estos se van bifurcando:
Cada elemento en el diagrama cuenta con una resistencia, una capacidad y una inductancia permitiendo una oscilaci n amortiguada.
El modelo tiene especial aplicaci n en situaciones de uso de ventiladores que generan una respiraci n forzada.
Diagrama de la oscilaci n de un modelo din mico para un pulm n bajo respiraci n forzada (caso de un adulto). En el se representa la impedancia, que corresponde a una medida de la resistencia, en funci n de la frecuencia de respiraci n:
La curva muestra un m nimo en que el pulm n es capaz de respirar con menor resistencias.
Dentro del modelo el ctrico la resistencia se puede modelar en funci n de par metros de la din mica de flujo de gases, resultando
donde
Dentro del modelo el ctrico la capacidad se puede modelar en funci n de par metros de la din mica de flujo de gases, resultando
donde
Dentro del modelo el ctrico la inductancia se puede modelar en funci n de par metros de la din mica de flujo de gases, resultando
donde
ID:(730, 0)
