Loading [MathJax]/extensions/tex2jax.js
Usuario: No hay usuarios registrado.


Redes de elementos hidráulicas
Storyboard

Si comparamos la ley de Darcy con la ley de Ohm en la electricidad, notamos una analogía en la que el flujo del líquido se asemeja a la corriente eléctrica, la diferencia de presión se relaciona con la diferencia de potencial y los elementos hidráulicos se comparan con sus resistencias hidráulicas, similar a las resistencias eléctricas.Esta analogía implica que, al igual que existen redes eléctricas, también se pueden definir redes hidráulicas en las cuales se calculan resistencias hidráulicas totales basadas en resistencias hidráulicas parciales.

>Modelo

ID:(1388, 0)


Mecanismos
Concepto


ID:(15729, 0)


Redes hidrodinámicas
Descripción

La resistencia hidráulica ($R_h$) de un elemento modelado como un tubo cilíndrico se puede calcular usando el largo de tubo ($\Delta L$), el radio del tubo ($R$) y la viscosidad ($\eta$) a través de la siguiente ecuación:

$ R_h =\displaystyle\frac{8 \eta | \Delta L | }{ \pi R ^4}$



y la conductancia hidráulica ($G_h$) se calcula mediante:

$ G_h =\displaystyle\frac{ \pi R ^4}{8 \eta | \Delta L | }$



estas se relacionan a través de:

$ R_h = \displaystyle\frac{1}{ G_h }$



Tanto la resistencia hidráulica ($R_h$) como la conductancia hidráulica ($G_h$) permiten establecer una relación entre el diferencial de la presión ($\Delta p$) y el flujo de volumen ($J_V$) utilizando:

$ \Delta p = R_h J_V $



o

$ J_V = G_h \Delta p $

ID:(11098, 0)


Suma de resistencias hidráulicas en serie
Descripción

En el caso de resistencias hidráulicas conectadas en serie:



la suma de la caída de ERROR:10132,0 en cada ERROR:9887,0 corresponde a la diferencia de presión total ($\Delta p_t$):

$ \Delta p_t =\displaystyle\sum_k \Delta p_k $



mientras que la resistencia hidráulica total en serie ($R_{st}$) se describe mediante:

$ R_{st} =\displaystyle\sum_k R_{hk} $



y la conductancia hidráulica total en serie ($G_{st}$) se define por:

$\displaystyle\frac{1}{ G_{st} }=\displaystyle\sum_k\displaystyle\frac{1}{ G_{hk} }$

ID:(15736, 0)


Proceso para la suma de resistencias hidráulicas en serie
Descripción

Primero se calculan los valores de la resistencia hidráulica en una red ($R_{hk}$) utilizando la viscosidad ($\eta$), el radio del cilindro k ($R_k$) y el largo de tubo k ($\Delta L_k$) mediante la ecuación:

$ R_h =\displaystyle\frac{8 \eta | \Delta L | }{ \pi R ^4}$



Luego se suman para obtener la resistencia hidráulica total en serie ($R_{st}$):

$ R_{st} =\displaystyle\sum_k R_{hk} $



Con este resultado, se puede calcular el flujo de volumen ($J_V$) para la diferencia de presión total ($\Delta p_t$) utilizando:

$ \Delta p_t = R_{st} J_V $



Una vez obtenido el flujo de volumen ($J_V$), se calcula la diferencia de presión en una red ($\Delta p_k$) mediante:

$ \Delta p_k = R_{hk} J_V $



Para el caso de tres resistencias, el cálculo se puede visualizar en la siguiente gráfica:

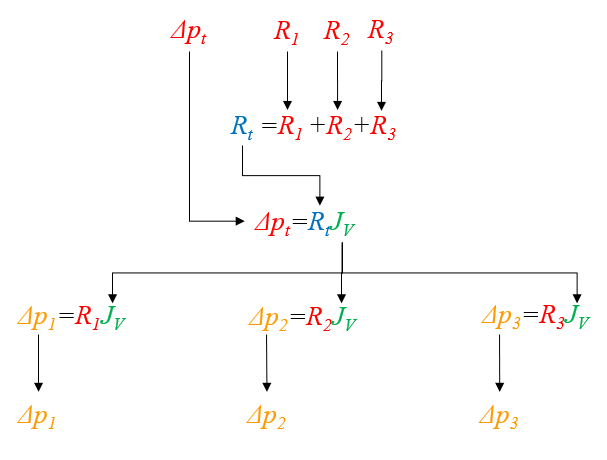
ID:(11069, 0)


Suma de resistencias hidráulicas en paralelo
Descripción

En el caso de resistencias hidráulicas conectadas en paralelo:



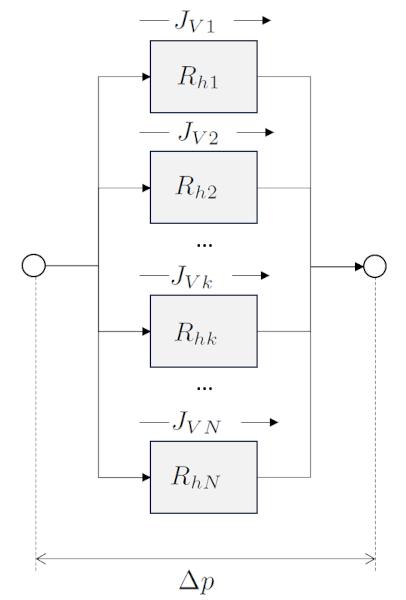
la suma del flujo de ERROR:10133,0 en cada ERROR:9887,0 corresponde a el flujo de volumen total ($J_{Vt}$):

$ J_{Vt} =\displaystyle\sum_k J_{Vk} $



mientras que la resistencia hidráulica total en paralelo ($R_{pt}$) se describe mediante:

$\displaystyle\frac{1}{ R_{pt} }=\sum_k\displaystyle\frac{1}{ R_{hk} }$



y la conductancia hidráulica total en paralelo ($G_{pt}$) se define por:

$ G_{pt} =\displaystyle\sum_k G_{hk} $

ID:(15737, 0)


Proceso para la suma de resistencias hidráulicas en paralelo
Descripción

Primero, se calculan los valores de la resistencia hidráulica en una red ($R_{hk}$) utilizando las variables la viscosidad ($\eta$), el radio del cilindro k ($R_k$) y el largo de tubo k ($\Delta L_k$) a través de la ecuación:

$ R_h =\displaystyle\frac{8 \eta | \Delta L | }{ \pi R ^4}$



Estos valores se suman para obtener la resistencia hidráulica total en serie ($R_{st}$):

$\displaystyle\frac{1}{ R_{pt} }=\sum_k\displaystyle\frac{1}{ R_{hk} }$



Con este resultado, es posible calcular el diferencial de la presión ($\Delta p$) para la resistencia hidráulica total en paralelo ($R_{pt}$) utilizando:

$ \Delta p = R_{pt} J_{Vt} $



Una vez determinado el diferencial de la presión ($\Delta p$), se procede a calcular el flujo de volumen en una red ($J_{Vk}$) a través de:

$ \Delta p = R_{hk} J_{Vk} $



Para el caso de tres resistencias, el cálculo se puede representar en la siguiente gráfica:

ID:(11070, 0)


Modelo
Concepto


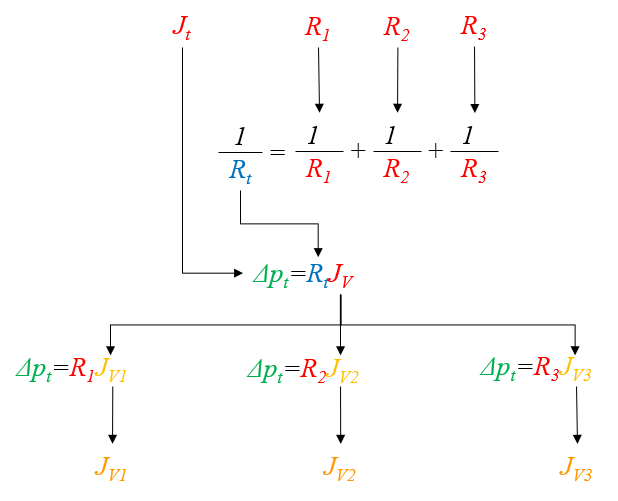
ID:(15734, 0)


Redes de elementos hidráulicas
Modelo

Si comparamos la ley de Darcy con la ley de Ohm en la electricidad, notamos una analogía en la que el flujo del líquido se asemeja a la corriente eléctrica, la diferencia de presión se relaciona con la diferencia de potencial y los elementos hidráulicos se comparan con sus resistencias hidráulicas, similar a las resistencias eléctricas. Esta analogía implica que, al igual que existen redes eléctricas, también se pueden definir redes hidráulicas en las cuales se calculan resistencias hidráulicas totales basadas en resistencias hidráulicas parciales.

Variables
Símbolo
Texto
Variable
Valor
Unidades
Calcule
Valor MKS
Unidades MKS
$G_h$
G_h
Conductancia hidráulica
m^4s/kg
$G_{hk}$
G_hk
Conductancia hidráulica en una red
m^4s/kg
$G_{pt}$
G_pt
Conductancia hidráulica total en paralelo
m^4s/kg
$G_{st}$
G_st
Conductancia hidráulica total en serie
m^4s/kg
$\Delta p_k$
Dp_k
Diferencia de presión en una red
Pa
$\Delta p_t$
Dp_t
Diferencia de presión total
Pa
$\Delta p$
Dp
Diferencial de la presión
Pa
$J_V$
J_V
Flujo de volumen
m^3/s
$J_{Vk}$
J_Vk
Flujo de volumen en una red
m^3/s
$J_{Vt}$
J_Vt
Flujo de volumen total
m^3/s
$\Delta L$
DL
Largo de tubo
m
$R$
R
Radio del tubo
m
$R_h$
R_h
Resistencia hidráulica
kg/m^4s
$R_{hk}$
R_hk
Resistencia hidráulica en una red
kg/m^4s
$R_{pt}$
R_pt
Resistencia hidráulica total en paralelo
kg/m^4s
$R_{st}$
R_st
Resistencia hidráulica total en serie
kg/m^4s
$\eta$
eta
Viscosidad
Pa s

Cálculos

Primero, seleccione la ecuación:   a ,  luego, seleccione la variable:   a 
Dp = R_h * J_V Dp = R_h * J_V Dp = R_h * J_V Dp = R_h * J_V Dp = R_h * J_V R_st =@SUM( R_hk , k ) 1/ R_pt =@SUM( 1/ R_hk , k ) R_h =8* eta * abs( DL )/( pi * R ^4) 1/ G_st = @SUM( 1/ G_hk, k ) G_pt = @SUM( G_hk , k ) J_Vt =sum_k J_Vk Dp_t =sum_k Dp_k J_V = G_h * Dp R_h = 1/ G_h R_h = 1/ G_h R_h = 1/ G_h R_h = 1/ G_h G_h = pi * R ^4/(8* eta * abs( DL ))G_hG_hkG_ptG_stDp_kDp_tDpJ_VJ_VkJ_VtDLRR_hR_hkR_ptR_steta
Símbolo
Ecuación
Resuelto
Traducido

Cálculos

Símbolo
Ecuación
Resuelto
Traducido

 Variable   Dado   Calcule   Objetivo :   Ecuación   A utilizar
Dp = R_h * J_V Dp = R_h * J_V Dp = R_h * J_V Dp = R_h * J_V Dp = R_h * J_V R_st =@SUM( R_hk , k ) 1/ R_pt =@SUM( 1/ R_hk , k ) R_h =8* eta * abs( DL )/( pi * R ^4) 1/ G_st = @SUM( 1/ G_hk, k ) G_pt = @SUM( G_hk , k ) J_Vt =sum_k J_Vk Dp_t =sum_k Dp_k J_V = G_h * Dp R_h = 1/ G_h R_h = 1/ G_h R_h = 1/ G_h R_h = 1/ G_h G_h = pi * R ^4/(8* eta * abs( DL ))G_hG_hkG_ptG_stDp_kDp_tDpJ_VJ_VkJ_VtDLRR_hR_hkR_ptR_steta


Ecuaciones

El flujo de volumen ($J_V$) se puede determinar a partir de la conductancia hidráulica ($G_h$) y la diferencia de presión ($\Delta p$) utilizando la ecuaci n siguiente:

$ J_V = G_h \Delta p $



Adem s, utilizando la relaci n para la resistencia hidráulica ($R_h$):

$ R_h = \displaystyle\frac{1}{ G_h }$



se obtiene el resultado final:

$ \Delta p = R_h J_V $

(ID 3179)

El flujo de volumen ($J_V$) se puede determinar a partir de la conductancia hidráulica ($G_h$) y la diferencia de presión ($\Delta p$) utilizando la ecuaci n siguiente:

$ J_V = G_h \Delta p $



Adem s, utilizando la relaci n para la resistencia hidráulica ($R_h$):

$ R_h = \displaystyle\frac{1}{ G_h }$



se obtiene el resultado final:

$ \Delta p = R_h J_V $

(ID 3179)

El flujo de volumen ($J_V$) se puede determinar a partir de la conductancia hidráulica ($G_h$) y la diferencia de presión ($\Delta p$) utilizando la ecuaci n siguiente:

$ J_V = G_h \Delta p $



Adem s, utilizando la relaci n para la resistencia hidráulica ($R_h$):

$ R_h = \displaystyle\frac{1}{ G_h }$



se obtiene el resultado final:

$ \Delta p = R_h J_V $

(ID 3179)

El flujo de volumen ($J_V$) se puede determinar a partir de la conductancia hidráulica ($G_h$) y la diferencia de presión ($\Delta p$) utilizando la ecuaci n siguiente:

$ J_V = G_h \Delta p $



Adem s, utilizando la relaci n para la resistencia hidráulica ($R_h$):

$ R_h = \displaystyle\frac{1}{ G_h }$



se obtiene el resultado final:

$ \Delta p = R_h J_V $

(ID 3179)

El flujo de volumen ($J_V$) se puede determinar a partir de la conductancia hidráulica ($G_h$) y la diferencia de presión ($\Delta p$) utilizando la ecuaci n siguiente:

$ J_V = G_h \Delta p $



Adem s, utilizando la relaci n para la resistencia hidráulica ($R_h$):

$ R_h = \displaystyle\frac{1}{ G_h }$



se obtiene el resultado final:

$ \Delta p = R_h J_V $

(ID 3179)

Una forma de modelar un tubo en el que var a la secci n es dividirlo en secciones de radio constante y luego sumar las resistencias hidr ulicas en serie. Supongamos que tenemos una serie de la resistencia hidráulica en una red ($R_{hk}$), que depende de la viscosidad ($\eta$), el radio del cilindro k ($R_k$) y el largo de tubo k ($\Delta L_k$) a trav s de la siguiente ecuaci n:

$ R_h =\displaystyle\frac{8 \eta | \Delta L | }{ \pi R ^4}$



En cada elemento habr una diferencia de presión en una red ($\Delta p_k$) con la resistencia hidráulica en una red ($R_{hk}$) y el flujo de volumen ($J_V$) para los que se aplica la ley de Darcy

$ \Delta p_k = R_{hk} J_V $



la diferencia de presión total ($\Delta p_t$) ser igual a la suma de las ERROR:10132,0 individuales

$ \Delta p_t =\displaystyle\sum_k \Delta p_k $



por lo que

$\Delta p_t=\displaystyle\sum_k \Delta p_k=\displaystyle\sum_k (R_{hk}J_V)=\left(\displaystyle\sum_k R_{hk}\right)J_V\equiv R_{st}J_V$



Por lo tanto, el sistema se puede modelar como un conducto nico con la resistencia hidr ulica calculada como la suma de las componentes individuales:

$ R_{st} =\displaystyle\sum_k R_{hk} $

(ID 3180)

La conductancia hidráulica total en paralelo ($G_{pt}$) junto con la conductancia hidráulica en una red ($G_{hk}$) en

$ G_{pt} =\displaystyle\sum_k G_{hk} $



y junto con la resistencia hidráulica en una red ($R_{hk}$) y la ecuaci n

$ R_{st} = \displaystyle\frac{1}{ G_{st} }$



conduce a la resistencia hidráulica total en paralelo ($R_{pt}$) mediante

$\displaystyle\frac{1}{ R_{pt} }=\sum_k\displaystyle\frac{1}{ R_{hk} }$

(ID 3181)

Dado que la resistencia hidráulica ($R_h$) es igual a la conductancia hidráulica ($G_h$) seg n la siguiente ecuaci n:

$ R_h = \displaystyle\frac{1}{ G_h }$



y dado que la conductancia hidráulica ($G_h$) se expresa en t rminos de la viscosidad ($\eta$), el radio del tubo ($R$) y el largo de tubo ($\Delta L$) de la siguiente manera:

$ G_h =\displaystyle\frac{ \pi R ^4}{8 \eta | \Delta L | }$



podemos concluir que:

$ R_h =\displaystyle\frac{8 \eta | \Delta L | }{ \pi R ^4}$

(ID 3629)

La resistencia hidráulica total en serie ($R_{st}$), junto con la resistencia hidráulica en una red ($R_{hk}$) en

$ R_{st} =\displaystyle\sum_k R_{hk} $



y junto con la conductancia hidráulica en una red ($G_{hk}$) y la ecuaci n

$ R_{st} = \displaystyle\frac{1}{ G_{st} }$



conduce a que la conductancia hidráulica total en serie ($G_{st}$) se puede calcular con:

$\displaystyle\frac{1}{ G_{st} }=\displaystyle\sum_k\displaystyle\frac{1}{ G_{hk} }$

(ID 3633)

Con el flujo total ($J_{Vt}$) siendo igual a el flujo de volumen en una red ($J_{Vk}$):

$ J_{Vt} =\displaystyle\sum_k J_{Vk} $



y con la diferencia de presión ($\Delta p$) y la conductancia hidráulica en una red ($G_{hk}$), junto con la ecuaci n

$ J_V = G_h \Delta p $



para cada elemento, podemos deducir que, con la conductancia hidráulica total en paralelo ($G_{pt}$),

$J_{Vt}=\displaystyle\sum_k J_{Vk} = \displaystyle\sum_k G_{hk}\Delta p = G_{pt}\Delta p$



lo que implica que

$ G_{pt} =\displaystyle\sum_k G_{hk} $

.

(ID 3634)

Si observamos la ley de Hagen-Poiseuille, que nos permite calcular el flujo de volumen ($J_V$) a partir de el radio del tubo ($R$), la viscosidad ($\eta$), el largo de tubo ($\Delta L$) y la diferencia de presión ($\Delta p$):

$ J_V =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$



podemos introducir la conductancia hidráulica ($G_h$) definido en t rminos de el largo de tubo ($\Delta L$), el radio del tubo ($R$) y la viscosidad ($\eta$) de la siguiente manera:

$ G_h =\displaystyle\frac{ \pi R ^4}{8 \eta | \Delta L | }$



y as obtener:

$ J_V = G_h \Delta p $

(ID 14471)

Ejemplos


(ID 15729)

La resistencia hidráulica ($R_h$) de un elemento modelado como un tubo cil ndrico se puede calcular usando el largo de tubo ($\Delta L$), el radio del tubo ($R$) y la viscosidad ($\eta$) a trav s de la siguiente ecuaci n:

$ R_h =\displaystyle\frac{8 \eta | \Delta L | }{ \pi R ^4}$



y la conductancia hidráulica ($G_h$) se calcula mediante:

$ G_h =\displaystyle\frac{ \pi R ^4}{8 \eta | \Delta L | }$



estas se relacionan a trav s de:

$ R_h = \displaystyle\frac{1}{ G_h }$



Tanto la resistencia hidráulica ($R_h$) como la conductancia hidráulica ($G_h$) permiten establecer una relaci n entre el diferencial de la presión ($\Delta p$) y el flujo de volumen ($J_V$) utilizando:

$ \Delta p = R_h J_V $



o

$ J_V = G_h \Delta p $

(ID 11098)

En el caso de resistencias hidr ulicas conectadas en serie:



la suma de la ca da de ERROR:10132,0 en cada ERROR:9887,0 corresponde a la diferencia de presión total ($\Delta p_t$):

$ \Delta p_t =\displaystyle\sum_k \Delta p_k $



mientras que la resistencia hidráulica total en serie ($R_{st}$) se describe mediante:

$ R_{st} =\displaystyle\sum_k R_{hk} $



y la conductancia hidráulica total en serie ($G_{st}$) se define por:

$\displaystyle\frac{1}{ G_{st} }=\displaystyle\sum_k\displaystyle\frac{1}{ G_{hk} }$

(ID 15736)

Primero se calculan los valores de la resistencia hidráulica en una red ($R_{hk}$) utilizando la viscosidad ($\eta$), el radio del cilindro k ($R_k$) y el largo de tubo k ($\Delta L_k$) mediante la ecuaci n:

$ R_h =\displaystyle\frac{8 \eta | \Delta L | }{ \pi R ^4}$



Luego se suman para obtener la resistencia hidráulica total en serie ($R_{st}$):

$ R_{st} =\displaystyle\sum_k R_{hk} $



Con este resultado, se puede calcular el flujo de volumen ($J_V$) para la diferencia de presión total ($\Delta p_t$) utilizando:

$ \Delta p_t = R_{st} J_V $



Una vez obtenido el flujo de volumen ($J_V$), se calcula la diferencia de presión en una red ($\Delta p_k$) mediante:

$ \Delta p_k = R_{hk} J_V $



Para el caso de tres resistencias, el c lculo se puede visualizar en la siguiente gr fica:

(ID 11069)

En el caso de resistencias hidr ulicas conectadas en paralelo:



la suma del flujo de ERROR:10133,0 en cada ERROR:9887,0 corresponde a el flujo de volumen total ($J_{Vt}$):

$ J_{Vt} =\displaystyle\sum_k J_{Vk} $



mientras que la resistencia hidráulica total en paralelo ($R_{pt}$) se describe mediante:

$\displaystyle\frac{1}{ R_{pt} }=\sum_k\displaystyle\frac{1}{ R_{hk} }$



y la conductancia hidráulica total en paralelo ($G_{pt}$) se define por:

$ G_{pt} =\displaystyle\sum_k G_{hk} $

(ID 15737)

Primero, se calculan los valores de la resistencia hidráulica en una red ($R_{hk}$) utilizando las variables la viscosidad ($\eta$), el radio del cilindro k ($R_k$) y el largo de tubo k ($\Delta L_k$) a trav s de la ecuaci n:

$ R_h =\displaystyle\frac{8 \eta | \Delta L | }{ \pi R ^4}$



Estos valores se suman para obtener la resistencia hidráulica total en serie ($R_{st}$):

$\displaystyle\frac{1}{ R_{pt} }=\sum_k\displaystyle\frac{1}{ R_{hk} }$



Con este resultado, es posible calcular el diferencial de la presión ($\Delta p$) para la resistencia hidráulica total en paralelo ($R_{pt}$) utilizando:

$ \Delta p = R_{pt} J_{Vt} $



Una vez determinado el diferencial de la presión ($\Delta p$), se procede a calcular el flujo de volumen en una red ($J_{Vk}$) a trav s de:

$ \Delta p = R_{hk} J_{Vk} $



Para el caso de tres resistencias, el c lculo se puede representar en la siguiente gr fica:

(ID 11070)


(ID 15734)

ID:(1388, 0)