Druyd:Knowledge

Ley de Darcy

Storyboard

La ley de Hagen-Poiseuille para el flujo total se puede expresar en términos de una diferencia de presión, el flujo y un factor que puede ser definido como una resistencia hidráulica, lo que da origen a lo que conocemos como la ley de Darcy.

>Modelo

ID:(877, 0)

Mecanismos

Concepto

ID:(15721, 0)

Flujo laminar por un tubo

Concepto

Cuando se expone un tubo lleno de líquido con ERROR:5422,0 a la presión en la posición inicial ( $p_i$ ) en el posición al inicio del tubo ( $L_i$ ) y la presión en la posición final (e) ( $p_e$ ) en el posición al final del tubo ( $L_e$ ), se genera una diferencia de presión ( $\Delta p_s$ ) a lo largo de el largo de tubo ( $\Delta L$ ), lo que da como resultado el perfil de la velocidad en un radio del cilindro ( $v$ ):

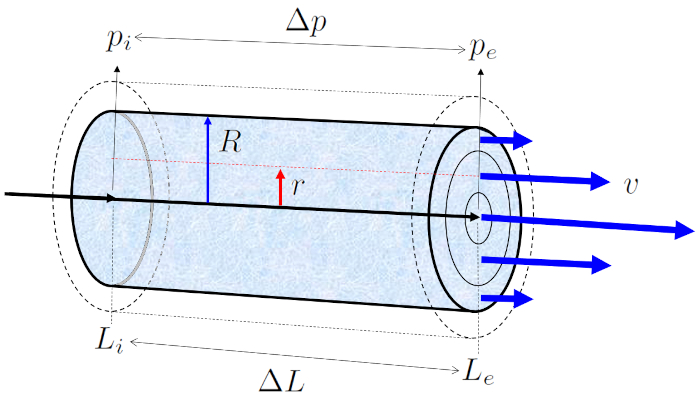
En flujos con valores bajos de el número de Reynold ( $Re$ ), donde la viscosidad es más significativa que la inercia del líquido, el flujo se desarrolla de manera laminar, es decir, sin la presencia de turbulencias.

ID:(2218, 0)

Flujo según ecuación de Hagen-Poiseuille

Concepto

El perfil de la velocidad en un radio del cilindro ( $v$ ) en el radio de la posición en un tubo ( $r$ ) permite calcular el flujo de volumen ( $J_V$ ) en un tubo mediante una integración de toda la superficie, lo que nos conduce a la conocida ley de Hagen-Poiseuille.

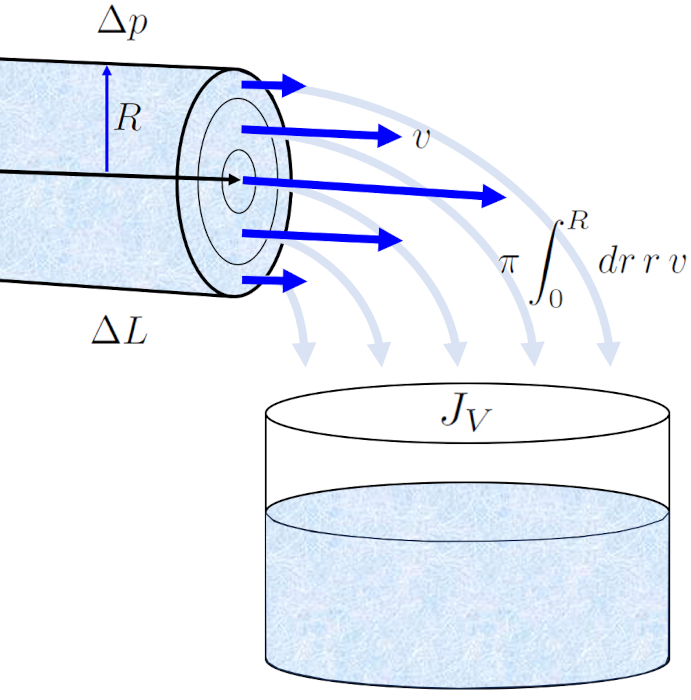
El resultado es una ecuación que depende de ERROR:5417,0 elevado a la cuarta potencia. No obstante, es fundamental tener en cuenta que este perfil de flujo solo se mantiene en caso de que el flujo sea laminar.

Con ello, se deduce de la viscosidad ( $\eta$ ) que el flujo de volumen ( $J_V$ ) ante un largo de tubo ( $\Delta L$ ) y un diferencial de la presión ( $\Delta p$ ) la expresión:

$J_V =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$

Los articulos originales que dieron origen a esta ley con un nombre combinado fueron: "Ueber die Gesetze, welche des der Strom des Wassers in röhrenförmigen Gefässen bestimmen" (Sobre las leyes que rigen el flujo del agua en recipientes cilíndricos), Gotthilf Hagen, Annalen der Physik und Chemie 46:423442 (1839) "Recherches expérimentales sur le mouvement des liquides dans les tubes de très-petits diamètres" (Investigación experimental sobre el movimiento de líquidos en tubos de diámetros muy pequeños), Jean-Louis-Marie Poiseuille, Comptes Rendus de l'Académie des Sciences 9:433544 (1840).

ID:(2216, 0)

Ley de Darcy y conductancia hidráulica

Concepto

Si observamos la ley de Hagen-Poiseuille, que nos permite calcular el flujo de volumen ( $J_V$ ) a partir de el radio del tubo ( $R$ ), la viscosidad ( $\eta$ ), el largo de tubo ( $\Delta L$ ) y la diferencia de presión ( $\Delta p$ ):

$J_V =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$

podemos introducir la conductancia hidráulica ( $G_h$ ) definido en términos de el largo de tubo ( $\Delta L$ ), el radio del tubo ( $R$ ) y la viscosidad ( $\eta$ ) de la siguiente manera:

$G_h =\displaystyle\frac{ \pi R ^4}{8 \eta | \Delta L | }$

y así obtener:

$J_V = G_h \Delta p$

ID:(15723, 0)

Resistencia hidráulica de un tubo

Concepto

Dado que la resistencia hidráulica ( $R_h$ ) es igual a la conductancia hidráulica ( $G_h$ ) según la siguiente ecuación:

$R_h = \displaystyle\frac{1}{ G_h }$

y dado que la conductancia hidráulica ( $G_h$ ) se expresa en términos de la viscosidad ( $\eta$ ), el radio del tubo ( $R$ ) y el largo de tubo ( $\Delta L$ ) de la siguiente manera:

$G_h =\displaystyle\frac{ \pi R ^4}{8 \eta | \Delta L | }$

podemos concluir que:

$R_h =\displaystyle\frac{8 \eta | \Delta L | }{ \pi R ^4}$

ID:(15724, 0)

Ley de Darcy y resistencia hidráulica

Concepto

El flujo de volumen ( $J_V$ ) se puede calcular a partir de la conductancia hidráulica ( $G_h$ ) y la diferencia de presión ( $\Delta p$ ) mediante la siguiente ecuación:

$J_V = G_h \Delta p$

Por otro lado con lado con la relación para la resistencia hidráulica ( $R_h$ )

$R_h = \displaystyle\frac{1}{ G_h }$

por lo que se obtiene

$\Delta p = R_h J_V$

que Henry Darcy formuló [1] para modelar el comportamiento general de medios porosos más complejos por los cuales fluye un líquido.La genialidad de esta forma de reescribir la ley de Hagen-Poiseuille es que muestra la analogía que existe entre el flujo de corriente eléctrica y el flujo de líquido. En este sentido, la ley de Hagen-Poiseuille corresponde a la ley de Ohm. Esto abre la posibilidad de aplicar los conceptos de redes eléctricas a sistemas de tuberías por donde fluye un líquido.Esta ley, también conocida como Ley de Darcy-Weisbach, fue publicada por primera vez en la obra de Darcy: [1] "Les fontaines publiques de la ville de Dijon" (Las Fuentes Públicas de la Ciudad de Dijon), Henry Darcy, Victor Dalmont Editeur, París (1856).

ID:(15720, 0)

Medición de la Ley de Darcy

Imagen

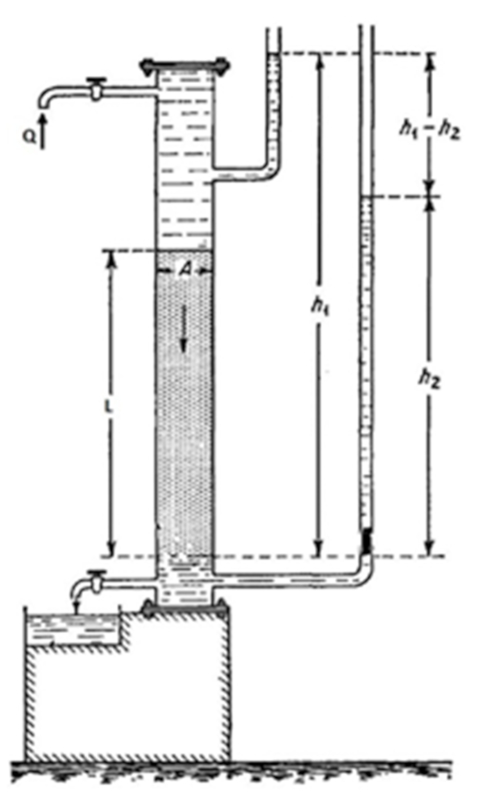
El experimento de Darcy involucra un cilindro lleno con un material a estudiar y un líquido de interés. En la parte inferior del cilindro, hay una válvula que regula la salida del líquido. Tanto en la parte superior como en la inferior, hay columnas de líquido asociadas para determinar las presiones presentes. De esta manera, se miden las presiones, la cantidad de líquido que fluye y el tiempo transcurrido, lo cual permite determinar la resistencia hidráulica.

ID:(11104, 0)

Modelo

Concepto

ID:(15722, 0)

Ley de Darcy

Modelo

Variables

Símbolo

Texto

Variable

Valor

Unidades

Calcule

Valor MKS

Unidades MKS

$G_h$

G_h

Conductancia hidráulica

m^4s/kg

$\Delta p$

Diferencial de la presión

$J_V$

J_V

Flujo de volumen

m^3/s

$\Delta L$

Largo de tubo

$R$

Radio del tubo

$R_h$

R_h

Resistencia hidráulica

kg/m^4s

$\eta$

eta

Viscosidad

Pa s

Cálculos

Ecuación

Número

Primero, seleccione la ecuación:

, luego, seleccione la variable:

Símbolo

Ecuación

Resuelto

Traducido

Cálculos

Símbolo

Ecuación

Resuelto

Traducido

Variable

Dado

Calcule

Objetivo :

Ecuación

A utilizar

Ecuaciones

$J_V =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$

J_V =- pi * R ^4* Dp /(8* eta * DL )

Si consideramos el perfil de ERROR:5449,0 de un fluido en un canal cil ndrico, donde la velocidad en un radio del cilindro ( $v$ ) var a en funci n de ERROR:10120,0 de acuerdo con la siguiente expresi n:

$v = v_{max} \left(1-\displaystyle\frac{ r ^2}{ R ^2}\right)$

con el radio del tubo ( $R$ ) y la velocidad máxima del flujo ( $v_{max}$ ). Podemos calcular la velocidad máxima del flujo ( $v_{max}$ ) utilizando la viscosidad ( $\eta$ ), la diferencia de presión ( $\Delta p$ ) y el largo de tubo ( $\Delta L$ ) de la siguiente manera:

$v_{max} =-\displaystyle\frac{ R ^2}{4 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$

Si integramos la velocidad en toda la secci n transversal del canal, obtendremos el flujo de volumen ( $J_V$ ), definida como la integral de $\pi r v(r)$ con respecto a ERROR:10120,0 desde $0$ hasta ERROR:5417,0. Esta integral se simplifica de la siguiente manera:

$J_V=-\displaystyle\int_0^Rdr \pi r v(r)=-\displaystyle\frac{R^2}{4\eta}\displaystyle\frac{\Delta p}{\Delta L}\displaystyle\int_0^Rdr \pi r \left(1-\displaystyle\frac{r^2}{R^2}\right)$

La integraci n nos lleva a la ley de Hagen-Poiseuille resultante:

$J_V =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$

(ID 3178)

$\Delta p = R_h J_V$

Dp = R_h * J_V

El flujo de volumen ( $J_V$ ) se puede determinar a partir de la conductancia hidráulica ( $G_h$ ) y la diferencia de presión ( $\Delta p$ ) utilizando la ecuaci n siguiente:

$J_V = G_h \Delta p$

Adem s, utilizando la relaci n para la resistencia hidráulica ( $R_h$ ):

$R_h = \displaystyle\frac{1}{ G_h }$

se obtiene el resultado final:

$\Delta p = R_h J_V$

(ID 3179)

$R_h =\displaystyle\frac{8 \eta | \Delta L | }{ \pi R ^4}$

R_h =8* eta * abs( DL )/( pi * R ^4)

Dado que la resistencia hidráulica ( $R_h$ ) es igual a la conductancia hidráulica ( $G_h$ ) seg n la siguiente ecuaci n:

$R_h = \displaystyle\frac{1}{ G_h }$

y dado que la conductancia hidráulica ( $G_h$ ) se expresa en t rminos de la viscosidad ( $\eta$ ), el radio del tubo ( $R$ ) y el largo de tubo ( $\Delta L$ ) de la siguiente manera:

$G_h =\displaystyle\frac{ \pi R ^4}{8 \eta | \Delta L | }$

podemos concluir que:

$R_h =\displaystyle\frac{8 \eta | \Delta L | }{ \pi R ^4}$

(ID 3629)

$J_V = G_h \Delta p$

J_V = G_h * Dp

$J_V =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$

podemos introducir la conductancia hidráulica ( $G_h$ ) definido en t rminos de el largo de tubo ( $\Delta L$ ), el radio del tubo ( $R$ ) y la viscosidad ( $\eta$ ) de la siguiente manera:

$G_h =\displaystyle\frac{ \pi R ^4}{8 \eta | \Delta L | }$

y as obtener:

$J_V = G_h \Delta p$

(ID 14471)

$R_h = \displaystyle\frac{1}{ G_h }$

R_h = 1/ G_h

(ID 15092)

$G_h =\displaystyle\frac{ \pi R ^4}{8 \eta | \Delta L | }$

G_h = pi * R ^4/(8* eta * abs( DL ))

(ID 15102)

Ejemplos

Mecanismos

(ID 15721)

Flujo laminar por un tubo

Cuando se expone un tubo lleno de l quido con ERROR:5422,0 a la presión en la posición inicial ( $p_i$ ) en el posición al inicio del tubo ( $L_i$ ) y la presión en la posición final (e) ( $p_e$ ) en el posición al final del tubo ( $L_e$ ), se genera una diferencia de presión ( $\Delta p_s$ ) a lo largo de el largo de tubo ( $\Delta L$ ), lo que da como resultado el perfil de la velocidad en un radio del cilindro ( $v$ ):

En flujos con valores bajos de el número de Reynold ( $Re$ ), donde la viscosidad es m s significativa que la inercia del l quido, el flujo se desarrolla de manera laminar, es decir, sin la presencia de turbulencias.

(ID 2218)

Flujo seg n ecuaci n de Hagen-Poiseuille

El perfil de la velocidad en un radio del cilindro ( $v$ ) en el radio de la posición en un tubo ( $r$ ) permite calcular el flujo de volumen ( $J_V$ ) en un tubo mediante una integraci n de toda la superficie, lo que nos conduce a la conocida ley de Hagen-Poiseuille.

El resultado es una ecuaci n que depende de ERROR:5417,0 elevado a la cuarta potencia. No obstante, es fundamental tener en cuenta que este perfil de flujo solo se mantiene en caso de que el flujo sea laminar.

Con ello, se deduce de la viscosidad ( $\eta$ ) que el flujo de volumen ( $J_V$ ) ante un largo de tubo ( $\Delta L$ ) y un diferencial de la presión ( $\Delta p$ ) la expresi n:

$J_V =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$

Los articulos originales que dieron origen a esta ley con un nombre combinado fueron: "Ueber die Gesetze, welche des der Strom des Wassers in r hrenf rmigen Gef ssen bestimmen" (Sobre las leyes que rigen el flujo del agua en recipientes cil ndricos), Gotthilf Hagen, Annalen der Physik und Chemie 46:423442 (1839) "Recherches exp rimentales sur le mouvement des liquides dans les tubes de tr s-petits diam tres" (Investigaci n experimental sobre el movimiento de l quidos en tubos de di metros muy peque os), Jean-Louis-Marie Poiseuille, Comptes Rendus de l'Acad mie des Sciences 9:433544 (1840).

(ID 2216)

Ley de Darcy y conductancia hidr ulica

$J_V =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$

podemos introducir la conductancia hidráulica ( $G_h$ ) definido en t rminos de el largo de tubo ( $\Delta L$ ), el radio del tubo ( $R$ ) y la viscosidad ( $\eta$ ) de la siguiente manera:

$G_h =\displaystyle\frac{ \pi R ^4}{8 \eta | \Delta L | }$

y as obtener:

$J_V = G_h \Delta p$

(ID 15723)

Resistencia hidr ulica de un tubo

Dado que la resistencia hidráulica ( $R_h$ ) es igual a la conductancia hidráulica ( $G_h$ ) seg n la siguiente ecuaci n:

$R_h = \displaystyle\frac{1}{ G_h }$

y dado que la conductancia hidráulica ( $G_h$ ) se expresa en t rminos de la viscosidad ( $\eta$ ), el radio del tubo ( $R$ ) y el largo de tubo ( $\Delta L$ ) de la siguiente manera:

$G_h =\displaystyle\frac{ \pi R ^4}{8 \eta | \Delta L | }$

podemos concluir que:

$R_h =\displaystyle\frac{8 \eta | \Delta L | }{ \pi R ^4}$

(ID 15724)

Ley de Darcy y resistencia hidr ulica

El flujo de volumen ( $J_V$ ) se puede calcular a partir de la conductancia hidráulica ( $G_h$ ) y la diferencia de presión ( $\Delta p$ ) mediante la siguiente ecuaci n:

$J_V = G_h \Delta p$

Por otro lado con lado con la relaci n para la resistencia hidráulica ( $R_h$ )

$R_h = \displaystyle\frac{1}{ G_h }$

por lo que se obtiene

$\Delta p = R_h J_V$

que Henry Darcy formul [1] para modelar el comportamiento general de medios porosos m s complejos por los cuales fluye un l quido.La genialidad de esta forma de reescribir la ley de Hagen-Poiseuille es que muestra la analog a que existe entre el flujo de corriente el ctrica y el flujo de l quido. En este sentido, la ley de Hagen-Poiseuille corresponde a la ley de Ohm. Esto abre la posibilidad de aplicar los conceptos de redes el ctricas a sistemas de tuber as por donde fluye un l quido.Esta ley, tambi n conocida como Ley de Darcy-Weisbach, fue publicada por primera vez en la obra de Darcy: [1] "Les fontaines publiques de la ville de Dijon" (Las Fuentes P blicas de la Ciudad de Dijon), Henry Darcy, Victor Dalmont Editeur, Par s (1856).

(ID 15720)

Medici n de la Ley de Darcy

El experimento de Darcy involucra un cilindro lleno con un material a estudiar y un l quido de inter s. En la parte inferior del cilindro, hay una v lvula que regula la salida del l quido. Tanto en la parte superior como en la inferior, hay columnas de l quido asociadas para determinar las presiones presentes. De esta manera, se miden las presiones, la cantidad de l quido que fluye y el tiempo transcurrido, lo cual permite determinar la resistencia hidr ulica.

(ID 11104)

Modelo

(ID 15722)

ID:(877, 0)