Druyd:Knowledge

Flujo laminar viscoso (Hagen Poiseuille)

Storyboard

Cuando consideramos un flujo laminar de un fluido viscoso a través de un tubo, se forma un patrón en el que la velocidad es máxima en el centro y nula en el borde. El flujo total está directamente relacionado con el perfil cilíndrico del radio elevado a la cuarta potencia y, a su vez, es inversamente proporcional a la viscosidad del fluido.

>Modelo

ID:(876, 0)

Mecanismos

Concepto

ID:(15491, 0)

Flujo laminar por un tubo

Concepto

Cuando se expone un tubo lleno de líquido con ERROR:5422,0 a la presión en la posición inicial ( $p_i$ ) en el posición al inicio del tubo ( $L_i$ ) y la presión en la posición final (e) ( $p_e$ ) en el posición al final del tubo ( $L_e$ ), se genera una diferencia de presión ( $\Delta p_s$ ) a lo largo de el largo de tubo ( $\Delta L$ ), lo que da como resultado el perfil de la velocidad en un radio del cilindro ( $v$ ):

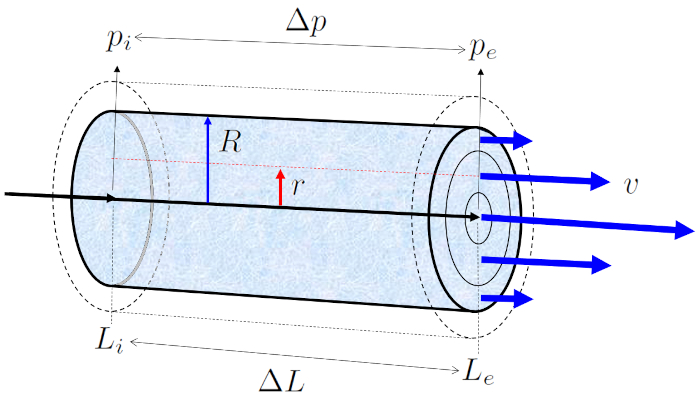
En flujos con valores bajos de el número de Reynold ( $Re$ ), donde la viscosidad es más significativa que la inercia del líquido, el flujo se desarrolla de manera laminar, es decir, sin la presencia de turbulencias.

ID:(2218, 0)

Láminas en la corriente

Concepto

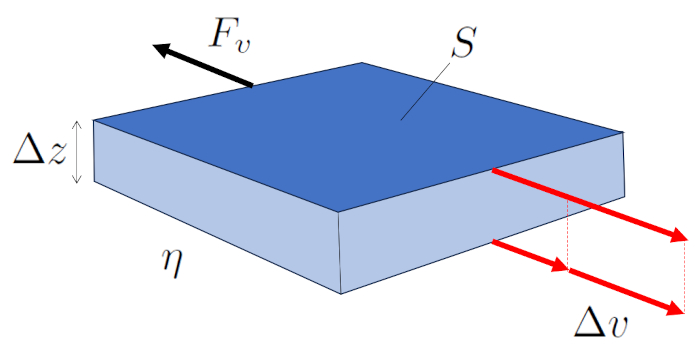
En el flujo laminar, capas contiguas se desplazan y existe una fuerza generada por la viscosidad entre ellas. La capa más rápida arrastra a su vecina más lenta, mientras que la más lenta restringe el avance de la más rápida.

Por lo tanto, la fuerza la fuerza viscosa ( $F_v$ ) generada por unas superficies paralelas ( $S$ ) sobre la otra es una función de una diferencia de velocidad entre superficies ( $\Delta v$ ), una distancia entre las superficies ( $\Delta z$ ) y una viscosidad ( $\eta$ ), como se muestra en la siguiente ecuación:

$F_v =- S \eta \displaystyle\frac{ \Delta v }{ \Delta z }$

y en el diagrama correspondiente:

ID:(7053, 0)

Flujo por un cilindro

Concepto

El flujo laminar alrededor de un cilindro se puede representar como múltiples capas cilíndricas que se deslizan bajo la influencia de las capas adyacentes. En ese caso, la fuerza viscosa ( $F_v$ ) con el largo de tubo ( $\Delta L$ ), la viscosidad ( $\eta$ ), y las variables la posición radial en cilindro ( $r$ ) y la velocidad en un radio del cilindro ( $v$ ) se expresa como:

$F_v =-2 \pi r \Delta L \eta \displaystyle\frac{ dv }{ dr }$

La capa en el borde a un radio del tubo ( $R$ ) no se mueve debido al efecto del borde y, a través de la viscosidad ( $\eta$ ), ralentiza la capa contigua que sí tiene velocidad.

El centro es la parte que se mueve a la velocidad máxima del flujo ( $v_{max}$ ), arrastrando a la capa que lo rodea. A su vez, esta capa arrastra a la siguiente y así sucesivamente hasta llegar a la capa en contacto con la pared del cilindro, que está detenida.

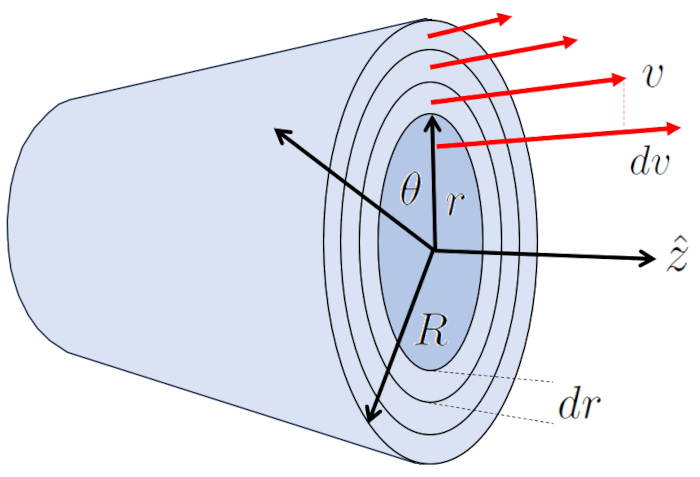
De esta manera, el sistema transfiere energía desde el centro hasta la pared, generando un perfil de velocidad representado por:

$v = v_{max} \left(1-\displaystyle\frac{ r ^2}{ R ^2}\right)$

con:

$v_{max} =-\displaystyle\frac{ R ^2}{4 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$

ID:(7057, 0)

Flujo para densidad de flujo no homogénea

Concepto

ID:(15719, 0)

Flujo según ecuación de Hagen-Poiseuille

Concepto

El perfil de la velocidad en un radio del cilindro ( $v$ ) en el radio de la posición en un tubo ( $r$ ) permite calcular el flujo de volumen ( $J_V$ ) en un tubo mediante una integración de toda la superficie, lo que nos conduce a la conocida ley de Hagen-Poiseuille.

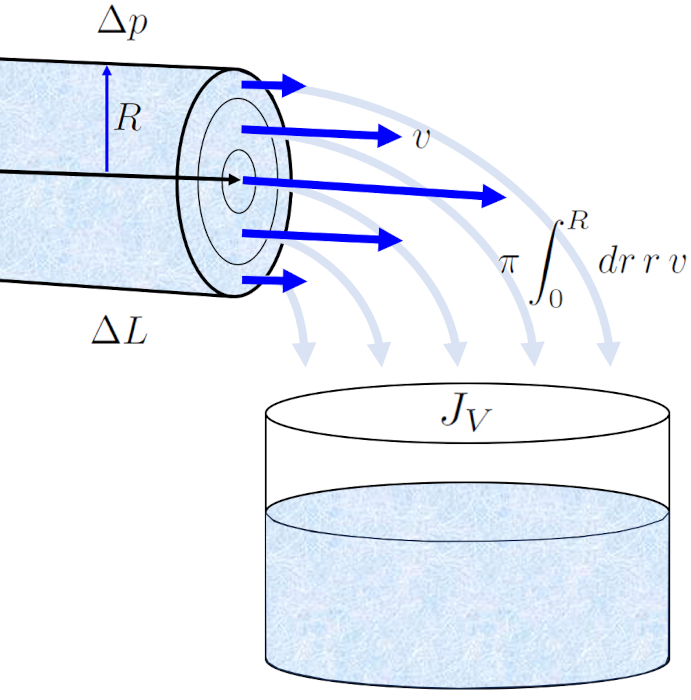
El resultado es una ecuación que depende de ERROR:5417,0 elevado a la cuarta potencia. No obstante, es fundamental tener en cuenta que este perfil de flujo solo se mantiene en caso de que el flujo sea laminar.

Con ello, se deduce de la viscosidad ( $\eta$ ) que el flujo de volumen ( $J_V$ ) ante un largo de tubo ( $\Delta L$ ) y un diferencial de la presión ( $\Delta p$ ) la expresión:

$J_V =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$

Los articulos originales que dieron origen a esta ley con un nombre combinado fueron: "Ueber die Gesetze, welche des der Strom des Wassers in röhrenförmigen Gefässen bestimmen" (Sobre las leyes que rigen el flujo del agua en recipientes cilíndricos), Gotthilf Hagen, Annalen der Physik und Chemie 46:423442 (1839) "Recherches expérimentales sur le mouvement des liquides dans les tubes de très-petits diamètres" (Investigación experimental sobre el movimiento de líquidos en tubos de diámetros muy pequeños), Jean-Louis-Marie Poiseuille, Comptes Rendus de l'Académie des Sciences 9:433544 (1840).

ID:(2216, 0)

Número de Reynold

Concepto

La inercia de un líquido se puede entender como proporcional a la densidad de energía cinética, dada por

$\displaystyle\frac{\rho_w}{2}v^2$

donde la densidad del líquido ( $\rho_w$ ) y la velocidad media del fluido ( $v$ ).

Si consideramos la la fuerza viscosa ( $F_v$ ) como

$F_v=S\eta\displaystyle\frac{v}{R}$

donde la sección o superficie ( $S$ ), la viscosidad ( $\eta$ ), la velocidad media del fluido ( $v$ ) y la dimensión típica del sistema ( $R$ ) del líquido.

Recordemos que la energía es igual a la la fuerza viscosa ( $F_v$ ) multiplicada por la el distancia recorrida ( $l$ ). La densidad de energía perdida por viscosidad será igual a la fuerza multiplicada por la distancia dividida por el volumen $S l$ :

$\displaystyle\frac{F_vl}{Sl}=S\eta\displaystyle\frac{v}{R}\displaystyle\frac{l}{Sl}=\eta\displaystyle\frac{v}{R}$

Por lo tanto, la relación entre la densidad de energía cinética y la densidad de energía viscosa es igual a un número adimensional, conocido como el número de Reynold ( $Re$ ). Cuando el número de Reynold ( $Re$ ) es mucho mayor que uno, la fuerza de inercia domina sobre la fuerza viscosa y el flujo se vuelve turbulento. Por otro lado, si el número de Reynold ( $Re$ ) es pequeño, la fuerza viscosa domina y el flujo se vuelve laminar.

$Re =\displaystyle\frac{ \rho R v }{ \eta }$

En resumen, el número de Reynold ( $Re$ ) es un parámetro adimensional que indica la relación entre la fuerza de inercia y la fuerza viscosa en un flujo. Si el número de Reynolds es mucho menor que uno ( $Re\ll 1$ ), la viscosidad domina y el flujo es laminar. Si el número de Reynolds es mayor que uno ( $Re\gg 1$ ), la inercia domina y el flujo es turbulento.El artículo original en el que Osborne Reynolds introduce el número que lleva su nombre es: "Investigación Experimental de las Circunstancias que Determinan si el Movimiento del Agua Debe Ser Directo o Sinuoso, y de la Ley de Resistencia en Canales Paralelos" (An Experimental Investigation of the Circumstances Which Determine Whether the Motion of Water Shall Be Direct or Sinuous, and of the Law of Resistance in Parallel Channels), Osborne Reynolds, Philosophical Transactions of the Royal Society of London, Vol. 174, pp. 935-982 (1883).

ID:(15507, 0)

Modelo

Concepto

ID:(15493, 0)

Flujo laminar viscoso

Modelo

Variables

Símbolo

Texto

Variable

Valor

Unidades

Calcule

Valor MKS

Unidades MKS

$\rho$

rho

Densidad

kg/m^3

$j_s$

j_s

Densidad de flujo

m/s

$\Delta p$

Diferencial de la presión

$J_V$

J_V

Flujo de volumen

m^3/s

$\Delta L$

Largo de tubo

$Re$

Número de Reynold

$L_e$

L_e

Posición al final del tubo

$L_i$

L_i

Posición al inicio del tubo

$r$

Posición radial en cilindro

$p_e$

p_e

Presión en la posición final (e)

$p_i$

p_i

Presión en la posición inicial

$R$

Radio del tubo

$S$

Sección del flujo

m^2

$v$

Velocidad en un radio del cilindro

m/s

$v_{max}$

v_max

Velocidad máxima del flujo

m/s

$\eta$

eta

Viscosidad

Pa s

Cálculos

Ecuación

Número

Primero, seleccione la ecuación:

, luego, seleccione la variable:

Símbolo

Ecuación

Resuelto

Traducido

Cálculos

Símbolo

Ecuación

Resuelto

Traducido

Variable

Dado

Calcule

Objetivo :

Ecuación

A utilizar

Ecuaciones

$Re =\displaystyle\frac{ \rho R v }{ \eta }$

Re = rho * R * v / eta

(ID 3177)

$J_V =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$

J_V =- pi * R ^4* Dp /(8* eta * DL )

Si consideramos el perfil de ERROR:5449,0 de un fluido en un canal cil ndrico, donde la velocidad en un radio del cilindro ( $v$ ) var a en funci n de ERROR:10120,0 de acuerdo con la siguiente expresi n:

$v = v_{max} \left(1-\displaystyle\frac{ r ^2}{ R ^2}\right)$

con el radio del tubo ( $R$ ) y la velocidad máxima del flujo ( $v_{max}$ ). Podemos calcular la velocidad máxima del flujo ( $v_{max}$ ) utilizando la viscosidad ( $\eta$ ), la diferencia de presión ( $\Delta p$ ) y el largo de tubo ( $\Delta L$ ) de la siguiente manera:

$v_{max} =-\displaystyle\frac{ R ^2}{4 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$

Si integramos la velocidad en toda la secci n transversal del canal, obtendremos el flujo de volumen ( $J_V$ ), definida como la integral de $\pi r v(r)$ con respecto a ERROR:10120,0 desde $0$ hasta ERROR:5417,0. Esta integral se simplifica de la siguiente manera:

$J_V=-\displaystyle\int_0^Rdr \pi r v(r)=-\displaystyle\frac{R^2}{4\eta}\displaystyle\frac{\Delta p}{\Delta L}\displaystyle\int_0^Rdr \pi r \left(1-\displaystyle\frac{r^2}{R^2}\right)$

La integraci n nos lleva a la ley de Hagen-Poiseuille resultante:

$J_V =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$

(ID 3178)

$v = v_{max} \left(1-\displaystyle\frac{ r ^2}{ R ^2}\right)$

v = v_max *(1- ( r / R )^2)

La diferencia de presión ( $\Delta p_s$ ) sobre una secci n de rea $\pi R^2$ , con el radio del tubo ( $R$ ) como el radio de la curvatura ( $r$ ), genera una fuerza que se representa como:

$\pi r^2 \Delta p$

Esta fuerza impulsa el l quido en contra de la resistencia viscosa, que est dada por:

$F_v =-2 \pi r \Delta L \eta \displaystyle\frac{ dv }{ dr }$

Igualando estas dos fuerzas, obtenemos:

$\pi r^2 \Delta p = \eta 2\pi r \Delta L \displaystyle\frac{dv}{dr}$

Lo que nos lleva a la ecuaci n:

$\displaystyle\frac{dv}{dr} = \displaystyle\frac{1}{2\eta}\displaystyle\frac{\Delta p}{\Delta L} r$

Si integramos esta ecuaci n desde una posici n definida por el radio de la curvatura ( $r$ ) hasta el borde donde el radio del tubo ( $R$ ) (teniendo en cuenta que la velocidad en el borde es nula), podemos obtener la velocidad en un radio del cilindro ( $v$ ) en funci n de el radio de la curvatura ( $r$ ):

$v = v_{max} \left(1-\displaystyle\frac{ r ^2}{ R ^2}\right)$

Donde:

$v_{max} =-\displaystyle\frac{ R ^2}{4 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$

es la la velocidad máxima del flujo ( $v_{max}$ ) en el centro del flujo.

(ID 3627)

$v_{max} =-\displaystyle\frac{ R ^2}{4 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$

v_max = - R ^2* Dp /(4* DL * eta )

(ID 3628)

$\Delta L = L_e - L_i$

DL = L_e - L_i

(ID 3802)

$S = \pi r ^2$

S = pi * r ^2

(ID 3804)

$j_s = \displaystyle\frac{ J_V }{ S }$

j_s = J_V / S

El flujo se define como el volumen el elemento de volumen ( $\Delta V$ ) dividido por el tiempo el tiempo transcurrido ( $\Delta t$ ), lo cual se expresa en la siguiente ecuaci n:

$J_V =\displaystyle\frac{ \Delta V }{ \Delta t }$

y el volumen es el producto de la secci n la sección del tubo ( $S$ ) por el desplazamiento el elemento del tubo ( $\Delta s$ ):

$\Delta V = S \Delta s$

Dado que el desplazamiento el elemento del tubo ( $\Delta s$ ) dividido por el tiempo el tiempo transcurrido ( $\Delta t$ ) equivale a la velocidad, se representa con:

$j_s =\displaystyle\frac{ \Delta s }{ \Delta t }$

Por lo tanto, el flujo es una densidad de flujo ( $j_s$ ), que se calcula mediante:

$j_s = \displaystyle\frac{ J_V }{ S }$

(ID 4349)

$\Delta p = p_e - p_i$

Dp = p_e - p_i

(ID 14459)

Ejemplos

Mecanismos

(ID 15491)

Flujo laminar por un tubo

Cuando se expone un tubo lleno de l quido con ERROR:5422,0 a la presión en la posición inicial ( $p_i$ ) en el posición al inicio del tubo ( $L_i$ ) y la presión en la posición final (e) ( $p_e$ ) en el posición al final del tubo ( $L_e$ ), se genera una diferencia de presión ( $\Delta p_s$ ) a lo largo de el largo de tubo ( $\Delta L$ ), lo que da como resultado el perfil de la velocidad en un radio del cilindro ( $v$ ):

En flujos con valores bajos de el número de Reynold ( $Re$ ), donde la viscosidad es m s significativa que la inercia del l quido, el flujo se desarrolla de manera laminar, es decir, sin la presencia de turbulencias.

(ID 2218)

L minas en la corriente

En el flujo laminar, capas contiguas se desplazan y existe una fuerza generada por la viscosidad entre ellas. La capa m s r pida arrastra a su vecina m s lenta, mientras que la m s lenta restringe el avance de la m s r pida.

Por lo tanto, la fuerza la fuerza viscosa ( $F_v$ ) generada por unas superficies paralelas ( $S$ ) sobre la otra es una funci n de una diferencia de velocidad entre superficies ( $\Delta v$ ), una distancia entre las superficies ( $\Delta z$ ) y una viscosidad ( $\eta$ ), como se muestra en la siguiente ecuaci n:

$F_v =- S \eta \displaystyle\frac{ \Delta v }{ \Delta z }$

y en el diagrama correspondiente:

(ID 7053)

Flujo por un cilindro

El flujo laminar alrededor de un cilindro se puede representar como m ltiples capas cil ndricas que se deslizan bajo la influencia de las capas adyacentes. En ese caso, la fuerza viscosa ( $F_v$ ) con el largo de tubo ( $\Delta L$ ), la viscosidad ( $\eta$ ), y las variables la posición radial en cilindro ( $r$ ) y la velocidad en un radio del cilindro ( $v$ ) se expresa como:

$F_v =-2 \pi r \Delta L \eta \displaystyle\frac{ dv }{ dr }$

La capa en el borde a un radio del tubo ( $R$ ) no se mueve debido al efecto del borde y, a trav s de la viscosidad ( $\eta$ ), ralentiza la capa contigua que s tiene velocidad.

El centro es la parte que se mueve a la velocidad máxima del flujo ( $v_{max}$ ), arrastrando a la capa que lo rodea. A su vez, esta capa arrastra a la siguiente y as sucesivamente hasta llegar a la capa en contacto con la pared del cilindro, que est detenida.

De esta manera, el sistema transfiere energ a desde el centro hasta la pared, generando un perfil de velocidad representado por:

$v = v_{max} \left(1-\displaystyle\frac{ r ^2}{ R ^2}\right)$

con:

$v_{max} =-\displaystyle\frac{ R ^2}{4 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$

(ID 7057)

Flujo para densidad de flujo no homog nea

En el caso de que la densidad de flujo ( $j_s$ ) sea constante, el flujo de volumen ( $J_V$ ) se puede calcular utilizando la sección o superficie ( $S$ ) de acuerdo con:

$J_V = S j_s$

Si la densidad de flujo ( $j_s$ ) var a, se pueden considerar elementos de secci n $dS$ lo suficientemente peque os para que la ecuaci n siga siendo v lida, en el sentido de que la contribuci n al flujo es:

$dJ_V = j_s dS$

Integrando esta expresi n sobre toda la secci n, se obtiene que

$J_V =\displaystyle\int j_s dS$

(ID 15719)

Flujo seg n ecuaci n de Hagen-Poiseuille

El perfil de la velocidad en un radio del cilindro ( $v$ ) en el radio de la posición en un tubo ( $r$ ) permite calcular el flujo de volumen ( $J_V$ ) en un tubo mediante una integraci n de toda la superficie, lo que nos conduce a la conocida ley de Hagen-Poiseuille.

El resultado es una ecuaci n que depende de ERROR:5417,0 elevado a la cuarta potencia. No obstante, es fundamental tener en cuenta que este perfil de flujo solo se mantiene en caso de que el flujo sea laminar.

Con ello, se deduce de la viscosidad ( $\eta$ ) que el flujo de volumen ( $J_V$ ) ante un largo de tubo ( $\Delta L$ ) y un diferencial de la presión ( $\Delta p$ ) la expresi n:

$J_V =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$

Los articulos originales que dieron origen a esta ley con un nombre combinado fueron: "Ueber die Gesetze, welche des der Strom des Wassers in r hrenf rmigen Gef ssen bestimmen" (Sobre las leyes que rigen el flujo del agua en recipientes cil ndricos), Gotthilf Hagen, Annalen der Physik und Chemie 46:423442 (1839) "Recherches exp rimentales sur le mouvement des liquides dans les tubes de tr s-petits diam tres" (Investigaci n experimental sobre el movimiento de l quidos en tubos de di metros muy peque os), Jean-Louis-Marie Poiseuille, Comptes Rendus de l'Acad mie des Sciences 9:433544 (1840).

(ID 2216)

N mero de Reynold

La inercia de un l quido se puede entender como proporcional a la densidad de energ a cin tica, dada por

$\displaystyle\frac{\rho_w}{2}v^2$

donde la densidad del líquido ( $\rho_w$ ) y la velocidad media del fluido ( $v$ ).

Si consideramos la la fuerza viscosa ( $F_v$ ) como

$F_v=S\eta\displaystyle\frac{v}{R}$

donde la sección o superficie ( $S$ ), la viscosidad ( $\eta$ ), la velocidad media del fluido ( $v$ ) y la dimensión típica del sistema ( $R$ ) del l quido.

Recordemos que la energ a es igual a la la fuerza viscosa ( $F_v$ ) multiplicada por la el distancia recorrida ( $l$ ). La densidad de energ a perdida por viscosidad ser igual a la fuerza multiplicada por la distancia dividida por el volumen $S l$ :

$\displaystyle\frac{F_vl}{Sl}=S\eta\displaystyle\frac{v}{R}\displaystyle\frac{l}{Sl}=\eta\displaystyle\frac{v}{R}$

Por lo tanto, la relaci n entre la densidad de energ a cin tica y la densidad de energ a viscosa es igual a un n mero adimensional, conocido como el número de Reynold ( $Re$ ). Cuando el número de Reynold ( $Re$ ) es mucho mayor que uno, la fuerza de inercia domina sobre la fuerza viscosa y el flujo se vuelve turbulento. Por otro lado, si el número de Reynold ( $Re$ ) es peque o, la fuerza viscosa domina y el flujo se vuelve laminar.

$Re =\displaystyle\frac{ \rho R v }{ \eta }$

En resumen, el número de Reynold ( $Re$ ) es un par metro adimensional que indica la relaci n entre la fuerza de inercia y la fuerza viscosa en un flujo. Si el n mero de Reynolds es mucho menor que uno ( $Re\ll 1$ ), la viscosidad domina y el flujo es laminar. Si el n mero de Reynolds es mayor que uno ( $Re\gg 1$ ), la inercia domina y el flujo es turbulento.El art culo original en el que Osborne Reynolds introduce el n mero que lleva su nombre es: "Investigaci n Experimental de las Circunstancias que Determinan si el Movimiento del Agua Debe Ser Directo o Sinuoso, y de la Ley de Resistencia en Canales Paralelos" (An Experimental Investigation of the Circumstances Which Determine Whether the Motion of Water Shall Be Direct or Sinuous, and of the Law of Resistance in Parallel Channels), Osborne Reynolds, Philosophical Transactions of the Royal Society of London, Vol. 174, pp. 935-982 (1883).

(ID 15507)

Modelo

(ID 15493)

ID:(876, 0)