Storyboard

One of the phase change processes is the evaporation process. In the liquid it absorbs energy by causing molecules of this to enter the state of gas that we call steam.

To model, we work with the Clausius Clapeyron equation that allows us to estimate the vapor pressure in equilibrium with the liquid.

>Model

ID:(316, 0)

Concept

>Top

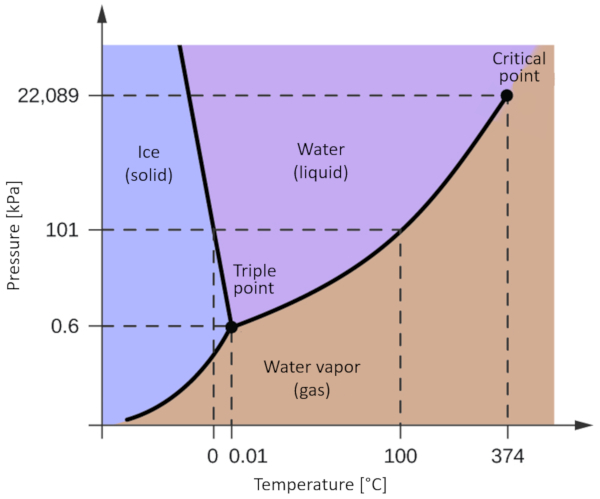
One of the most relevant phase diagrams for our planet is that of water. This diagram exhibits the three classical phases: solid, liquid, and gas, along with several phases featuring different crystalline structures of ice.

The significant distinction compared to other materials is that within a pressure range spanning from 611 Pa to 209.9 MPa, the solid phase occupies a greater volume than the liquid phase. This characteristic is reflected in the phase diagram as a negative slope along the boundary line separating the solid phase (hexagonal ice) and the liquid phase (water).

ID:(836, 0)

Image

>Top

Rudolf Clausius (1822-1888) was a German physicist and mathematician who made significant contributions to the field of thermodynamics. He is best known for formulating the second law of thermodynamics and for introducing the concept of entropy as a fundamental quantity in the study of energy transfer and transformation in physical systems.

ID:(1885, 0)

Description

>Top

One of the phenomena that also includes thermodynamics is the study of state changes. There are three basic states, gas, liquid and solid.

In the case of gas, the particles move almost freely and interact only with sporadic shocks.

In the case of a liquid the interaction is permanent. Despite this, the particles can be displaced without permanent unions towards the neighbors.

In the case of the solid, the interactions are such that the particles can no longer be displaced and only oscillate around a point of equilibrium defined by the neighboring particles.

The study of the changes of state tries to explain why the material passes in one form to the other and vice versa. In the case of medicine, these changes are relevant in processes where, for example, substances evaporate or dissolve. This both for the removal of materials and for temperature reduction such as perspiration.

ID:(147, 0)

Equation

>Top, >Model

Each phase change requires energy, energy needed to suspend the bonds between atoms or molecules of the material. When going from solid to liquid, solid to gas or liquid to gas, it is necessary to supply this energy. Otherwise, said energy must be removed from the system to achieve the phase change from gas to liquid, gas to solid or liquid to solid.

To measure the amount of heat that is required to evaporate a mass of liquid, we work with a device that measures the energy supplied (dissipated electrical energy) and the mass that is able to perform the phase change (weight):

In our case we are interested in the change of state of perspiration that allows a drastic elimination of heat from the surface of the body. In the upper part, by means of a heater, liquid is evaporated which is then counted to fall to the lower container which is heavy.

In this way it is found that there is a relationship between the evaporated mass \Delta m and the required energy or heat \Delta Q of the form

$ \Delta Q = L \Delta m$

Conditions

Variables

$\Delta m$

Evaporated Mass

$kg$

$L$

Latent Heat

$J/kg$

$\Delta Q$

Phase Change Heat

$J$

Relation

where L is the heat of evaporation or specific latent heat. In the case of water, the heat of evaporation is 538.9 kcal/kg.

ID:(3200, 0)

Equation

>Top, >Model

The differential of the Gibbs free energy ($dG$) can be calculated using the pressure Variation ($dp$) and the temperature variation ($dT$) in conjunction with the entropy ($S$) and the volume ($V$):

This equation remains constant along the lines separating phases during a phase change. This allows us to demonstrate the Clausius-Clapeyron Law with the assistance of the latent Heat ($L$), the absolute temperature ($T$), and the volume variation in phase change ($\Delta V$) [1,2,3]:

$\displaystyle\frac{ dp }{ dT }=\displaystyle\frac{ L }{ \Delta V T }$

Conditions

Variables

$T$

Absolute temperature

$K$

$L$

Latent Heat

$J/kg$

$dp$

Pressure Variation

$Pa$

$dT$

Temperature variation

$K$

$\Delta V$

Volume variation in phase change

$m^3$

Relation

Development

If the differential of the Gibbs free energy ($dG$) is constant, it means that for the pressure Variation ($dp$) and the temperature variation ($dT$), the values of the entropy ($S$) and the volume ($V$) in phase 1

$dG = -S_1dT+V_1dp$

and the entropy ($S$) and the volume ($V$) in phase 2

$dG = -S_2dT+V_2dp$

yield

$\displaystyle\frac{dp}{dT}=\displaystyle\frac{S_2-S_1}{V_2-V_1}$

The change in the entropy ($S$) between both phases corresponds to the latent Heat ($L$) divided by the absolute temperature ($T$):

$S_2 - S_1 =\displaystyle\frac{ L }{ T }$

So, with the definition of the volume variation in phase change ($\Delta V$)

$\Delta V \equiv V_2 - V_1$

we obtain

$\displaystyle\frac{ dp }{ dT }=\displaystyle\frac{ L }{ \Delta V T }$

[1] "Über die Art der Bewegung, welche wir Wärme nennen." (On the Nature of Motion We Call Heat), Rudolf Clausius, Annalen der Physik und Chemie, 155(6), 368-397. (1850)

[2] "Ueber eine veränderte Form des zweiten Hauptsatzes der mechanischen Wärmetheorie" (On a Modified Form of the Second Law of the Mechanical Theory of Heat), Rudolf Clausius, Annalen der Physik, 176(3), 353-400. (1857)

[3] "Mémoire sur la puissance motrice de la chaleur." (Memoir on the Motive Power of Heat), Benoît Paul Émile Clapeyron, Journal de l'École Royale Polytechnique, 14, 153-190. (1834)

ID:(12824, 0)

Description

>Top

Water is a special case since its phase diagram presents a key difference with respect to the vast majority of materials: the line that separates the solid and liquid phases has a negative slope.

This is due to the fact that the water changes from solid to liquid reduces its volume and with it the variation in volume $ \ Delta V $ is negative and the slope in the Clausius Clapeyron equation ends up being negative.

This property of water leads to the fact that if the temperature is lowered when it is in a liquid state $(dT,negative)$ upon reaching the phase change the pressure increases $ (dp) $ while in a normal liquid it is reduced . This is what leads to that in winter for example

freezing the water accumulated in the cracks and cracks of rocks in the mountains generates pressure which leads to its rupture and ultimately to the erosion of our geography.

When the surface of a lake freezes, the lake's water encapsulates, preventing it from expanding to form ice. This prevents lakes from freezing to the bottom while preserving life inside.

ID:(146, 0)

Equation

>Top, >Model

In many cases the latent molar heat is not available but the latent heat that is expressed, for example, in Joules per kilogram (J/Kg). Since the vapor pressure equation works with the latent molar heat we must convert the latent heat into latent molar heat. Since the latter is per mole, it is enough to divide the latent heat L by the molar mass M_m to obtain the latent molar heat

$ l_m \equiv\displaystyle\frac{ L }{ M_m }$

Conditions

Variables

$L$

Latent Heat

$J/kg$

$l_m$

Molar Latent Heat

$J/kg$

$M_m$

Molar Mass

$kg/mol$

Relation

In the case of water, the latent heat of evaporation is of the order of L\ sim 2,256\ times 10^6J/kg while the molar mass is M_m\sim 18,g/cm^3 = 0.018,kg/m^3, resulting in a latent molar heat of L_m\sim 40600,J/mol = 40.6,kJ/mol.

ID:(9273, 0)

Equation

>Top, >Model

The relationship between the concentration of water vapor molecules ($c_v$) and saturated water vapor concentration ($c_s$) is referred to as the relative humidity ($RH$). In other words, when a relative humidity of 100% is reached, the existing concentration will be equal to the saturated concentration.

$ RH =\displaystyle\frac{ c_v }{ c_s }$

Conditions

Variables

$c_v$

Concentration of water vapor molecules

$mol/m^3$

$RH$

Relative humidity

$-$

$c_s$

Saturated water vapor concentration

$mol/m^3$

Relation

ID:(3175, 0)

Equation

>Top, >Model

The change in volume between the material in two different states can be expressed in moles

$\Delta v_m =\displaystyle\frac{ \Delta V }{ M_m }$

Conditions

Variables

$M_m$

Molar Mass

$kg/mol$

$\Delta v_m$

Variation of molar volume during phase change

$m^3/mol$

$\Delta V$

Volume variation in phase change

$m^3$

Relation

to obtain a characteristic indicator of the material.

ID:(12823, 0)

Equation

>Top, >Model

The relationship between the concentration of water vapor molecules ($c_v$) and saturated water vapor concentration ($c_s$) is called the relative humidity ($RH$):

and it can be expressed in terms of the water vapor pressure unsaturated ($p_v$) and the pressure saturated water vapor ($p_s$) as follows:

$ RH =\displaystyle\frac{ p_v }{ p_s }$

Conditions

Variables

$p_s$

Pressure saturated water vapor

$Pa$

$RH$

Relative humidity

$-$

$p_v$

Water vapor pressure unsaturated

$Pa$

Relation

Development

The relationship between the relative humidity ($RH$) with the concentration of water vapor molecules ($c_v$) and saturated water vapor concentration ($c_s$) is expressed as:

$ RH =\displaystyle\frac{ c_v }{ c_s }$

and by relating the pressure ($p$) with the molar concentration ($c_m$), the absolute temperature ($T$), and the universal gas constant ($R$), we obtain:

$ p = c_m R T $

This applies to the vapor pressure of water, where:

$p_v = c_v R T$

and the saturated vapor pressure of water:

$p_s = c_s R T$

resulting in the following equation:

$ RH =\displaystyle\frac{ p_v }{ p_s }$

ID:(4478, 0)

Equation

>Top, >Model

The Clausius-Clapeyron equation [1,2,3], which depends on the pressure Variation ($dp$), the temperature variation ($dT$), the latent Heat ($L$), the volume variation in phase change ($\Delta V$), and the absolute temperature ($T$), is expressed as:

This equation can be rewritten in terms of the molar Latent Heat ($l_m$) and the variation of molar volume during phase change ($\Delta v_m$) as:

$\displaystyle\frac{ dp }{ dT }=\displaystyle\frac{ l_m }{ \Delta v_m T }$

Conditions

Variables

$T$

Absolute temperature

$K$

$l_m$

Molar Latent Heat

$J/kg$

$p$

Pressure

$Pa$

$\Delta v_m$

Variation of molar volume during phase change

$m^3/mol$

Relation

Development

With the Clausius-Clapeyron law, which depends on the pressure Variation ($dp$), the temperature variation ($dT$), the latent Heat ($L$), the volume variation in phase change ($\Delta V$), and the absolute temperature ($T$), expressed as:

$\displaystyle\frac{ dp }{ dT }=\displaystyle\frac{ L }{ \Delta V T }$

and the definition of the molar Latent Heat ($l_m$), where the latent Heat ($L$) is related to the molar Mass ($M_m$) as follows:

$ l_m \equiv\displaystyle\frac{ L }{ M_m }$

and the variation of molar volume during phase change ($\Delta v_m$), where the volume variation in phase change ($\Delta V$) is related to the molar Mass ($M_m$) as follows:

$\Delta v_m =\displaystyle\frac{ \Delta V }{ M_m }$

we obtain:

$\displaystyle\frac{ dp }{ dT }=\displaystyle\frac{ l_m }{ \Delta v_m T }$

[1] "Über die Art der Bewegung, welche wir Wärme nennen" (On the Nature of Motion Which We Call Heat), Rudolf Clausius, Annalen der Physik und Chemie, 155(6), 368-397. (1850)

[2] "Über eine veränderte Form des zweiten Hauptsatzes der mechanischen Wärmetheorie" (On a Modified Form of the Second Fundamental Theorem in the Mechanical Theory of Heat), Rudolf Clausius, Annalen der Physik, 176(3), 353-400. (1857)

[3] "Mémoire sur la puissance motrice de la chaleur" (Memoir on the Motive Power of Heat), Benoît Paul Émile Clapeyron, Journal de l'École Royale Polytechnique, 14, 153-190. (1834)

ID:(12822, 0)

Equation

>Top, >Model

When undergoing a phase change from a liquid to a gas, the change in volume can be expressed as:

$\Delta V = V_{\text{gas}} - V_{\text{liquid}}$

Since the volume of the gas is much greater than that of the liquid ( ($$)), we can approximate it as:

$\Delta V \approx V_{\text{gas}}$

As water vapor exhibits behavior similar to that of an ideal gas, we can state that with values the universal gas constant ($R$), the number of moles ($n$), the absolute temperature ($T$), and the water vapor pressure unsaturated ($p_v$):

$ \Delta V =\displaystyle\frac{ n R T }{ p_v }$

Conditions

Variables

$T$

Absolute temperature

$K$

$\Delta V$

Amount of Water Vapor

$m^3$

$n$

Número de Moles

$-$

$R$

Universal gas constant

8.4135

$J/mol K$

$p_v$

Water vapor pressure unsaturated

$Pa$

Relation

ID:(3185, 0)

Equation

>Top, >Model

Using the Clausius-Clapeyron equation for the gradient of the pressure ($p$) with respect to the absolute temperature ($T$), which depends on the molar Latent Heat ($l_m$) and the variation of molar volume during phase change ($\Delta v_m$):

and the ideal gas law, we can calculate the the pressure saturated water vapor ($p_s$) with respect to the reference pressure ($p_{ref}$) and the universal gas constant ($R$):

$ p_s = p_{ref} e^{- l_m / R T }$

Conditions

Variables

$T$

Absolute temperature

$K$

$l_m$

Molar Latent Heat

$J/kg$

$p_s$

Pressure saturated water vapor

$Pa$

$p_{ref}$

Reference pressure

3.65e+10

$Pa$

$R$

Universal gas constant

8.4135

$J/mol K$

Relation

Development

Using the Clausius-Clapeyron equation for the gradient of the pressure ($p$) with respect to the absolute temperature ($T$), which depends on the latent Heat ($L$) and the volume variation in phase change ($\Delta V$):

$\displaystyle\frac{ dp }{ dT }=\displaystyle\frac{ L }{ \Delta V T }$

In the case of the phase change from liquid to gas, we can assume that the change in volume is approximately equal to the volume of the vapor. Therefore, we can employ the ideal gas equation with the number of moles ($n$), the volume ($V$), the universal gas constant ($R$), and the water vapor pressure unsaturated ($p_v$):

$ \Delta V =\displaystyle\frac{ n R T }{ p_v }$

Since the Clausius-Clapeyron equation can be written as:

$\displaystyle\frac{dp}{dT}=\displaystyle\frac{L}{n}\displaystyle\frac{p}{R T^2}$

Where the molar Latent Heat ($l_m$) ($l_m = L/n$) corresponds to the change in enthalpy during the phase change h (the energy required to form water), we finally have:

$\displaystyle\frac{dp}{dT}=l_m\displaystyle\frac{p}{RT^2}$

If we integrate this equation between the pressure saturated water vapor ($p_s$) and the pressure at point p_0 at temperature T_0, we obtain:

$p_s=p_0e^{l_m/RT_0}e^{-l_m/RT}$

If we evaluate this expression with the data at the critical point:

$p_{ref}=p_0e^{l_m/RT_0}$

We finally have:

$ p_s = p_{ref} e^{- l_m / R T }$

the reference pressure ($p_{ref}$) can be calculated using data from both the triple point and the critical point. In the first case, the temperature is 0.01°C = 273.16K, and the pressure is 611.73 Pa. If the molar latent heat is 40.65 kJ/mol (for water), then the reference pressure ($p_{ref}$) has a value of 3.63E+10 Pa.

ID:(3182, 0)