User:


Uso de Lentes
Storyboard

>Model

ID:(292, 0)


Lens Geometry
Image

Corrección con Lentes

ID:(1864, 0)


Multiples lentes
Exercise

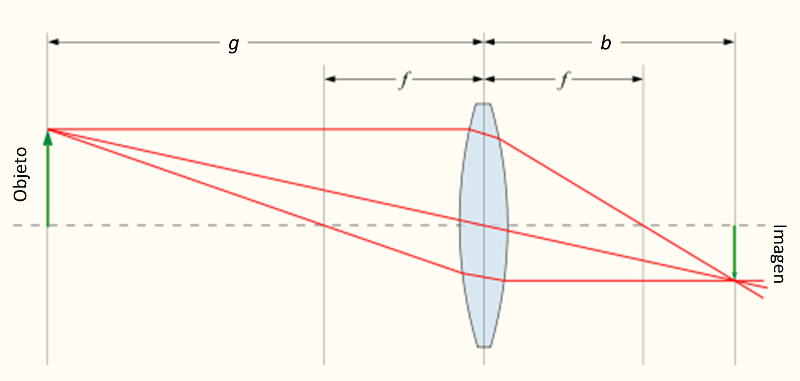
Cuando se acoplan dos lentes con sus respectivos focos, el primer lente genera una imagen que funciona como objeto para el segundo lente que a su vez genera una imagen de una imagen:

ID:(9465, 0)


Concave-Convex Lens Situation
Equation

Lente Convexo-Concavo grueso

ID:(1860, 0)


Convex-Concave Lens Situation
Script

Lente Concavo-Convexo grueso

ID:(1859, 0)


Diseño lente biconvexo
Variable

Lente Bi-Convexo grueso

ID:(1857, 0)


Situation of a Biconcave Lens
Audio

Lente Bi-Concavo grueso

ID:(1858, 0)


Uso de Lentes
Description

Variables
Symbol
Text
Variable
Value
Units
Calculate
MKS Value
MKS Units
$n$
n
Air-Lens Refractive Index
-
$D$
D
Dioptria
1/m
$s_b$
s_b
Distance Cristalino-Retina
m
$s_i$
s_i
Distance intermediate Lens Optical-Image
m
$s_o$
s_o
Distance Object-Lens Optical
m
$D$
D
Distance Optical-Crystalline Lens
m
$s_{lc}$
s_lc
Distancia de la imagen del lente cóncavo
m
$s_o$
s_o
Distancia del objeto al lente cóncavo
m
$f_{ccd}$
f_ccd
Foco del lente bi-cóncavo grueso
m
$f_{csd}$
f_csd
Foco del lente bi-cóncavo simétrico
m
$f_{vvd}$
f_vvd
Foco del lente bi-convexo grueso
m
$f_{vsd}$
f_vsd
Foco del lente bi-convexo simétrico
m
$f_{lc}$
f_lc
Foco del lente cóncavo
m
$f_{lv}$
f_lv
Foco del lente convexo
m
$f_{vcd}$
f_vcd
Foco del lente convexo-cóncavo grueso
m
$f_c$
f_c
Focus Eye Lens
m
$R$
R
Lens Radio
m
$d$
d
Lens Width
m
$a_o$
a_o
Object Size
m
$R_2$
R_2
Radio of the Lens, Image Side
m
$R_1$
R_1
Radio of the Lens, Source Side
m
$a_{lc}$
a_lc
Tamaño de la imagen en un lente cóncavo
m
$f_{cvs}$
f_cvs
Time
m

Calculations

First, select the equation:   to ,  then, select the variable:   to 
Symbol
Equation
Solved
Translated

Calculations

Symbol
Equation
Solved
Translated

 Variable   Given   Calculate   Target :   Equation   To be used


Equations

Una relaci n se puede armar con los tri ngulos del lado del objeto. En este caso la similitud nos permite escribir que el tama o del objeto a_o es a la distancia del objeto s_o al foco f es como el tama o de la imagen a_i es a la distancia del foco f:\\n\\n

$\displaystyle\frac{a_o}{s_o-f}=\displaystyle\frac{a_i}{f}$



Con la relaci n de similitud de los tri ngulos

$\displaystyle\frac{ a_o }{ a_{lc} }=\displaystyle\frac{ s_o }{ s_{lc} }$



se puede mostrar que se cumple:

$\displaystyle\frac{1}{ f_{lc} }=\displaystyle\frac{1}{ s_o }+\displaystyle\frac{1}{ s_{lc} }$

(ID 3347)

Como es

$\displaystyle\frac{1}{ f_{lv} }=\displaystyle\frac{1}{ s_o }+\displaystyle\frac{1}{ s_i }$

\\n\\nse tiene que\\n\\n

$ s_i = \displaystyle\frac{1}{\displaystyle\frac{1}{ f_l } - \displaystyle\frac{1}{ s_o }}$



con lo que

$\displaystyle\frac{1}{ f_c }=\displaystyle\frac{1}{ D - s_i }+ \displaystyle\frac{1}{ s_b }$



se obtiene

$\displaystyle\frac{1}{ s_o }+\displaystyle\frac{1}{ D -\displaystyle\frac{1}{\displaystyle\frac{1}{ f_{lv} }-\displaystyle\frac{1}{ s_b }}}=\displaystyle\frac{1}{ f_c }$

(ID 3355)

Examples

Correcci n con Lentes

(ID 1864)

Cuando se acoplan dos lentes con sus respectivos focos, el primer lente genera una imagen que funciona como objeto para el segundo lente que a su vez genera una imagen de una imagen:

(ID 9465)

Por similitud de los tri ngulos de los tama os del objeto y la imagen y las posiciones del objeto y foco permite por similitud de tri ngulos mostrar que:

$\displaystyle\frac{1}{ f_{lc} }=\displaystyle\frac{1}{ s_o }+\displaystyle\frac{1}{ s_{lc} }$

(ID 3347)

For any lens you can draw characteristic beams with which you can similarly show that the sizes of the object and the image are in the same proportion as their distances to the optical element (lens or mirror).

If the object has a size a_o, it is at a distance s_o of the lens, the image is a size a_i and is at a distance s_i, by similarity of the triangles it can be shown that

$\displaystyle\frac{ a_o }{ a_{lc} }=\displaystyle\frac{ s_o }{ s_{lc} }$

(ID 3346)

Si observamos la secci n imagen (entre lente y cristalino) - cristalino - imagen sobre la retina, se puede aplicar la relaci n entre foco f, distancia a objeto s_o y distancia a imagen s_i:

$\displaystyle\frac{1}{ f_{lc} }=\displaystyle\frac{1}{ s_o }+\displaystyle\frac{1}{ s_{lc} }$



En este caso no disponemos de la distancia entre imagen entre lente y cristalino y cristalino. Sin embargo se se define la la distancia entre lente y cristalino como D y se emplea la distancia entre lente ptico e imagen s_i se puede calcular la distancia entre imagen y cristalino de D-s_i. Como en este caso el foco es f_e y la distancia entre cristalino y retina es s_e se tiene que:

$\displaystyle\frac{1}{ f_c }=\displaystyle\frac{1}{ D - s_i }+ \displaystyle\frac{1}{ s_b }$

donde f_e es el foco del cristalino, D-s_i la distancia de la imagen creada por el lente ptico y s_e la distancia donde el lente ptico proyecta la imagen. En este caso la distancia s_e es la distancia entre cristalino y retina.

(ID 3354)

De la ecuaci n para el foco del lente ptico f_l

$\displaystyle\frac{1}{ f_{lv} }=\displaystyle\frac{1}{ s_o }+\displaystyle\frac{1}{ s_i }$



y la del cristalino f_e

$\displaystyle\frac{1}{ f_c }=\displaystyle\frac{1}{ D - s_i }+ \displaystyle\frac{1}{ s_b }$



la distancia entre lente y cristalino D y las distancias entre objeto y lente s_o y entre cristalino y retina s_e se puede eliminar la distancia de la imagen s_i y calcular directamente el foco del lente ptico que se necesita:

$\displaystyle\frac{1}{ s_o }+\displaystyle\frac{1}{ D -\displaystyle\frac{1}{\displaystyle\frac{1}{ f_{lv} }-\displaystyle\frac{1}{ s_b }}}=\displaystyle\frac{1}{ f_c }$

donde f_l es el foco del lente ptico, s_o la distancia al objeto al lente ptico y s_i la distancia donde el lente ptico proyecta la imagen.

(ID 3355)

Si observamos la secci n objeto - lente ptico - imagen (entre lente y cristalino) se puede aplicar la relaci n entre foco f, distancia a objeto s_o y distancia a imagen s_i:

$\displaystyle\frac{1}{ f_{lc} }=\displaystyle\frac{1}{ s_o }+\displaystyle\frac{1}{ s_{lc} }$



Si en este caso el foco es f_l, la distancia al objeto es s_o y la distancia lente a imagen s_i se tiene que:

$\displaystyle\frac{1}{ f_{lv} }=\displaystyle\frac{1}{ s_o }+\displaystyle\frac{1}{ s_i }$

donde f_l es el foco del lente ptico, s_o la distancia al objeto al lente ptico y s_i la distancia donde el lente ptico proyecta la imagen.

(ID 3353)

$D=\displaystyle\frac{1}{f}$

(ID 3449)

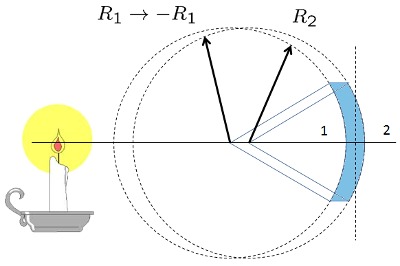
Lente Convexo-Concavo grueso

(ID 1860)

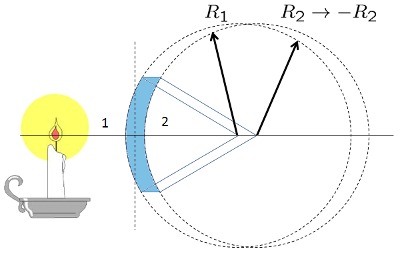
Lente Concavo-Convexo grueso

(ID 1859)

Una caso especial es aquel en que los radios son iguales, o sea R=R_1=R_2. Por ello el foco se calcula de:

$\displaystyle\frac{1}{ f_{vsd} }=( n -1)\left(\displaystyle\frac{2}{ R }-\displaystyle\frac{( n -1) d }{ n R ^2}\right)$

(ID 3432)

Los lentes reales tienen un grosor que se debe considerar. Si el lente tiene un indice de refracci n n, un grosor en el centro de d y las curvaturas son R_1 y R_2, el foco f se calcula con

$\displaystyle\frac{1}{ f_{vvd} }=( n -1)\left(\displaystyle\frac{1}{ R_1 }+\displaystyle\frac{1}{ R_2 }-\displaystyle\frac{( n -1)d}{ n R_1 R_2 }\right)$

(ID 3348)

Una caso especial es aquel en que los radios son iguales, o sea R=R_1=R_2. Por ello el foco se calcula de:

$\displaystyle\frac{1}{ f_{vcs} }=\displaystyle\frac{( n -1)^2 d }{ n R ^2}$

(ID 3430)

Los lentes reales tienen un grosor que se debe considerar. Si el lente tiene vidrio con indice de refracci n n, un grosor en el centro de d y las curvaturas son R_1 y R_2, se puede calcular el foco f. Para ello basta tomar la ecuaci n del lente bi-convexo e introducir el radios de curvatura R_2 con el signo negativo:

$\displaystyle\frac{1}{ f_{vcs} }=( n -1)\left(\displaystyle\frac{1}{ R_1 }-\displaystyle\frac{1}{ R_2 }+\displaystyle\frac{( n -1) d }{ n R_1 R_2 }\right)$

(ID 3350)

Lente Bi-Convexo grueso

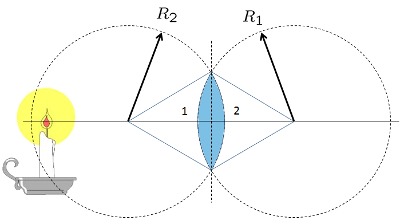
(ID 1857)

Lente Bi-Concavo grueso

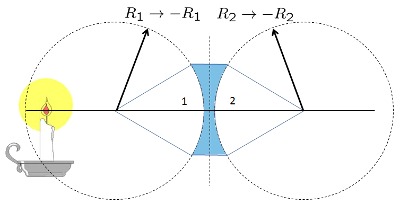
(ID 1858)

Una caso especial es aquel en que los radios son iguales, o sea R=R_1=R_2. Por ello el foco se calcula de:

$\displaystyle\frac{1}{ f_{csd} }=-( n -1)\left(\displaystyle\frac{2}{ R } +\displaystyle\frac{( n -1) d }{ n R ^2}\right)$

(ID 3431)

Una caso especial es aquel en que los radios son iguales, o sea R=R_1=R_2. Por ello el foco se calcula de:

$\displaystyle\frac{1}{ f_{cvs} }=\displaystyle\frac{( n -1)^2 d }{ n R ^2}$

(ID 3429)

Los lentes reales tienen un grosor que se debe considerar. Si el lente tiene vidrio con indice de refracci n n, un grosor en el centro de d y las curvaturas son R_1 y R_2, se puede calcular el foco f. Para ello basta tomar la ecuaci n del lente bi-convexo e introducir los radios de curvatura con el signo negativo:

$\displaystyle\frac{1}{ f_{ccd} }=-( n -1)\left(\displaystyle\frac{1}{ R_1 }+\displaystyle\frac{1}{ R_2 }+\displaystyle\frac{( n -1)d}{ n R_1 R_2 }\right)$

(ID 3349)

ID:(292, 0)