Perception of Distance
Definition 
We have two eyes so that we are able to estimate distances and thus have a three-dimensional perception.
ID:(433, 0)
Modeling the View of an Object
Note 
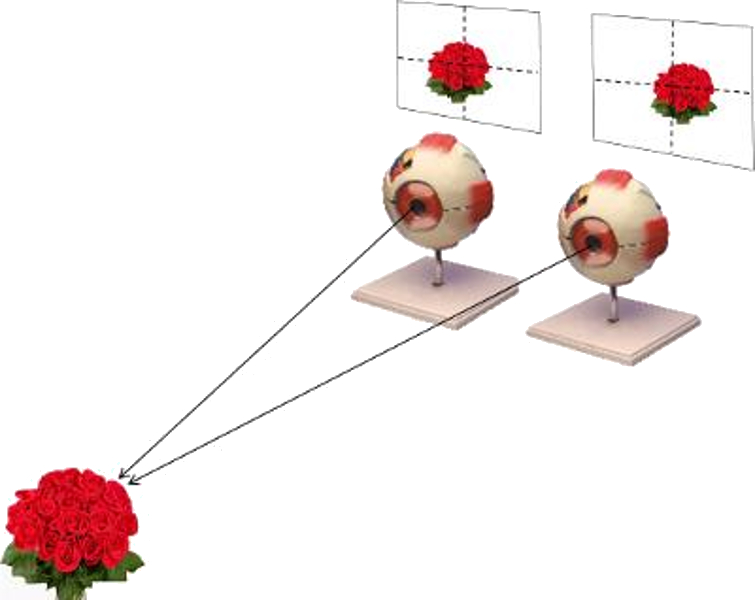
To model, we must diagram the situation that occurs with the images in both retinas. To do this, we studied the behavior of two beams in the plane formed between the object and the two retinas.
Suppose that the positions of the image in the left and right eye are
ID:(436, 0)
Geometry for Distance Measurement with the Eye
Quote 
The position of an object is perceived differently by each eye. The image is formed in different points with respect to the center of the retina:

From the difference in position we are able to determine the position of the object with respect to us.
ID:(1665, 0)
Equation Triangle Left Eye
Exercise 
By similarity of the triangles the proportion of the triangles of the left eye can be equalized. In the case of the major triangle the sides have lengths
ID:(434, 0)
Equation Triangle Right Eye
Equation 
By similarity of the triangles the proportion of the triangles of the right eye can be equated. In the case of the major triangle, the sides have lengths
ID:(435, 0)
Error on Distances Estimation
Script 
The error of the estimate can be calculated by using the uncertainty propagation equations on the expression for the calculation of the distance. To simplify the calculation we can use the expression for the case that the object is in front of us.
ID:(193, 0)
Medir Distancias
Storyboard 
Variables
Calculations
Calculations
Equations
Examples
We have two eyes so that we are able to estimate distances and thus have a three-dimensional perception.
Effect of seeing with two eyes
To model, we must diagram the situation that occurs with the images in both retinas. To do this, we studied the behavior of two beams in the plane formed between the object and the two retinas.
Suppose that the positions of the image in the left and right eye are
The position of an object is perceived differently by each eye. The image is formed in different points with respect to the center of the retina:
From the difference in position we are able to determine the position of the object with respect to us.
By similarity of the triangles the proportion of the triangles of the left eye can be equalized. In the case of the major triangle the sides have lengths
By similarity of the triangles the proportion of the triangles of the right eye can be equated. In the case of the major triangle, the sides have lengths
From the equations of the triangle of the left and right eye we can determine the distance of the object in the plane of the eyes
Note: it can be shown that the sum
The distance of the object can be determined from the equations of the left and right eye triangle. In this way we obtain that the distance Note: it can be shown that the sum
To return to what is the real distance
To return to what is the real distance
The error of the estimate can be calculated by using the uncertainty propagation equations on the expression for the calculation of the distance. To simplify the calculation we can use the expression for the case that the object is in front of us.
To simplify the solution of the model it is advisable to avoid working with the angle
The projected distance of the object is
Said change corresponds to moving from polar coordinates (
To return to what is the real distance
$\Delta r=\displaystyle\frac{2r^2}{df}$
$r= \sqrt{D^2+F^2}$
$F=r\sin\theta$
$r=\displaystyle\frac{df}{2s}$
$\displaystyle\frac{\Delta r^2}{r^2}=\displaystyle\frac{\Delta s^2}{s^2}+\displaystyle\frac{\Delta d^2}{d^2}+\displaystyle\frac{\Delta f^2}{f^2}$
ID:(291, 0)