Usuario:


Controlando la Luz
Storyboard

>Modelo

ID:(424, 0)


Paso entre medios de distintas velocidad de la luz
Definición

Cuando la luz en un medio con velocidad de la luz c_i alcanza una medio con una velocidad de la luz c_e el haz en en parte reflejado y en parte transmitido.

La transmisión sin embargo no solo puede perder intensidad, por la fracción reflejada, también puede ser desviada. Este desvío se denomina refracción.

ID:(429, 0)


Toda la luz es reflejada
Imagen

ID:(1851, 0)


Refracción de la luz
Ejercicio

ID:(1853, 0)


Controlando la Luz
Descripción

Variables
Símbolo
Texto
Variable
Valor
Unidades
Calcule
Valor MKS
Unidades MKS
$\theta_i$
theta_i
Angulo de incidente
rad
$\theta_c$
theta_c
Angulo de reflexión total
rad
$\theta_r$
theta_r
Angulo de refracción
rad
$d$
d
Desplazamiento del haz
m
$h$
h
Grosor del medio
m
$n$
n
Indice de refracción de un medio
-
$n_i$
n_i
Indice de refracción en el medio incidente
-
$n_e$
n_e
Indice de refracción paso del medio en que se refracta
-
$c$
c
Velocidad de la luz
m/s
$v$
v
Velocidad de la luz en el medio
m/s

Cálculos

Primero, seleccione la ecuación:   a ,  luego, seleccione la variable:   a 
Símbolo
Ecuación
Resuelto
Traducido

Cálculos

Símbolo
Ecuación
Resuelto
Traducido

 Variable   Dado   Calcule   Objetivo :   Ecuación   A utilizar


Ecuaciones

Como la relaci n entre los ngulos de incidencia y refracci n es

$\displaystyle\frac{ \sin \theta_i }{\sin \theta_r }=\displaystyle\frac{ c_i }{ c_e }$



y el indice de refracci n se define como

$ n =\displaystyle\frac{ c }{ v }$

\\n\\nse tiene que con\\n\\n

$n_i=\displaystyle\frac{c}{c_i}$

y\\n\\n

$n_e=\displaystyle\frac{c}{c_e}$

\\n\\nque\\n\\n

$\displaystyle\frac{c_i}{c_e}=\displaystyle\frac{c_i}{c}\displaystyle\frac{c}{c_e}=\displaystyle\frac{n_e}{n_i}=\displaystyle\frac{\sin\theta_i}{\sin\theta_e}$



por lo que resulta

$ n_i \sin \theta_i = n_e \sin \theta_r $

(ID 3343)

En el caso de reflexi n total el ngulo de refracci n es \theta_e=\pi/2 y con ello el seno igual a uno. Empleando la ley de Snell

$ n_i \sin \theta_i = n_e \sin \theta_r $

\\n\\npodemos calcular el ngulo de incidencia \theta_i, que definimos como ngulo cr tico \theta_c, con:\\n\\n

$n_i\sin\theta_c=n_e$



por lo que se puede escribir

$\sin \theta_c =\displaystyle\frac{ n_e }{ n_i }$

(ID 3344)

Ejemplos

Cuando la luz en un medio con velocidad de la luz c_i alcanza una medio con una velocidad de la luz c_e el haz en en parte reflejado y en parte transmitido.

La transmisi n sin embargo no solo puede perder intensidad, por la fracci n reflejada, tambi n puede ser desviada. Este desv o se denomina refracci n.

(ID 429)

Cuando se pasa de un medio en que la velocidad de la luz es menor a uno que es mayor existe la situaci n de que a un ngulo de incidencia muy grande no existe un correspondiente angulo de refracci n. En estos casos la luz solo se refleja y hablamos de reflexi n total.

En la siguiente imagen se ven distintos haces que al llegar a ser muy grande el angulo comienzan a sufrir reflexi n total:

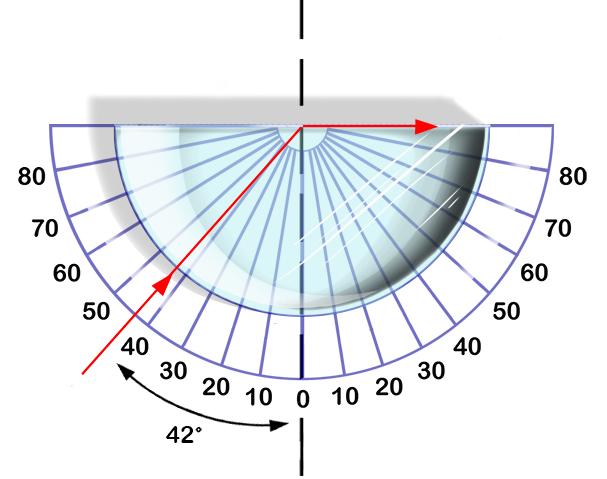
Paso por un vidrio

(ID 1851)

Paso de medio con mayor a menor velocidad

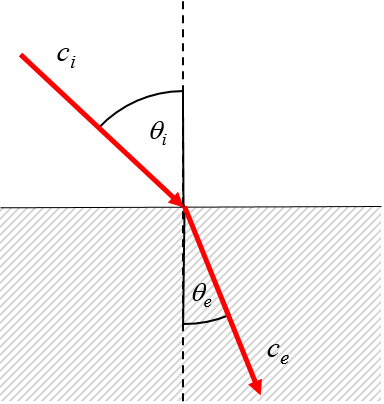
Paso del vac o, donde la velocidad de la luz es c a un medio con velocidad v

(ID 1849)

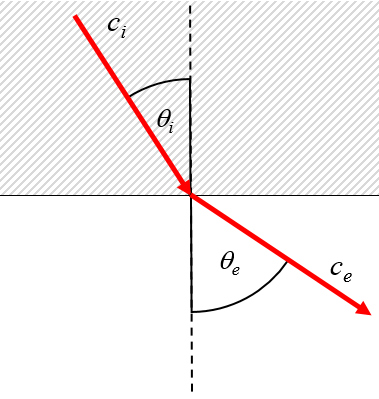
Cuando un haz pasa de un medio de menor velocidad v_i a uno con mayor v_e su direcci n se altera de modo que el angulo de incidencia \theta_i se agranda:

Paso de un medio, donde la velocidad de la luz v, al vac o.

(ID 1850)

Paso de la luz por un objeto

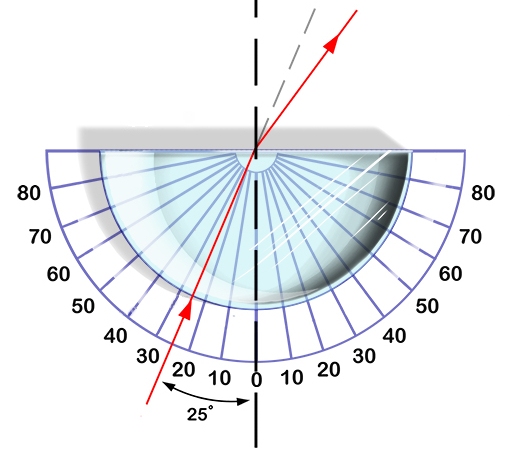
Paso por un vidrio

(ID 1853)

ID:(424, 0)