Viscosidad de la sangre según el modelo de Einstein
Definición 
Si se compara la viscosidad de la sangre medida con aquella estimada con la ecuación de Einstein se observa el siguiente comportamiento:

ID:(1694, 0)
Adherencia de glóbulos en la pared
Imagen 
Cuando los glóbulos se adhieren a las paredes de los vasos tienden a enangostar el vaso. Este fenómeno se denomina el efecto Fahraeus-Lindqvist y se muestra a continuación

Glóbulos adheridos a la pared
ID:(1896, 0)
Deformación de las plaquetas
Cita 
La deformación de los hematocitos lleva a que se vuelven mas hidrodinámicos con lo que se reduce la resistencia.

ID:(1695, 0)
Efecto de la Viscosidad
Descripción 
Variables
Cálculos
Cálculos
Ecuaciones
Si consideramos el perfil de ERROR:5449,0 de un fluido en un canal cil ndrico, donde la velocidad en un radio del cilindro ($v$) var a en funci n de ERROR:10120,0 de acuerdo con la siguiente expresi n:
| $ v = v_{max} \left(1-\displaystyle\frac{ r ^2}{ R ^2}\right)$ |
con el radio del tubo ($R$) y la velocidad máxima del flujo ($v_{max}$). Podemos calcular la velocidad máxima del flujo ($v_{max}$) utilizando la viscosidad ($\eta$), la diferencia de presión ($\Delta p$) y el largo de tubo ($\Delta L$) de la siguiente manera:
| $ v_{max} =-\displaystyle\frac{ R ^2}{4 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
Si integramos la velocidad en toda la secci n transversal del canal, obtendremos el flujo de volumen ($J_V$), definida como la integral de $\pi r v(r)$ con respecto a ERROR:10120,0 desde $0$ hasta ERROR:5417,0. Esta integral se simplifica de la siguiente manera:
$J_V=-\displaystyle\int_0^Rdr \pi r v(r)=-\displaystyle\frac{R^2}{4\eta}\displaystyle\frac{\Delta p}{\Delta L}\displaystyle\int_0^Rdr \pi r \left(1-\displaystyle\frac{r^2}{R^2}\right)$
La integraci n nos lleva a la ley de Hagen-Poiseuille resultante:
| $ J_V =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
(ID 3178)
Como
| $ F_v =- S \eta \displaystyle\frac{ \Delta v }{ \Delta z }$ |
y las superficies paralelas ($S$) es
$S=2\pi r \Delta L$
donde el radio de la posición en un tubo ($r$) y el largo de tubo ($\Delta L$), con lo que la la fuerza de resistencia en cilindro ($F_v$) es
| $ F_v =-2 \pi r \Delta L \eta \displaystyle\frac{ dv }{ dr }$ |
donde la viscosidad ($\eta$), la variación de la velocidad entre dos radios ($dv$) y el variación del radio en un tubo ($dr$).
(ID 3623)
La diferencia de presión ($\Delta p_s$) sobre una secci n de rea $\pi R^2$, con el radio del tubo ($R$) como el radio de la curvatura ($r$), genera una fuerza que se representa como:
$\pi r^2 \Delta p$
Esta fuerza impulsa el l quido en contra de la resistencia viscosa, que est dada por:
| $ F_v =-2 \pi r \Delta L \eta \displaystyle\frac{ dv }{ dr }$ |
Igualando estas dos fuerzas, obtenemos:
$\pi r^2 \Delta p = \eta 2\pi r \Delta L \displaystyle\frac{dv}{dr}$
Lo que nos lleva a la ecuaci n:
$\displaystyle\frac{dv}{dr} = \displaystyle\frac{1}{2\eta}\displaystyle\frac{\Delta p}{\Delta L} r$
Si integramos esta ecuaci n desde una posici n definida por el radio de la curvatura ($r$) hasta el borde donde el radio del tubo ($R$) (teniendo en cuenta que la velocidad en el borde es nula), podemos obtener la velocidad en un radio del cilindro ($v$) en funci n de el radio de la curvatura ($r$):
| $ v = v_{max} \left(1-\displaystyle\frac{ r ^2}{ R ^2}\right)$ |
Donde:
| $ v_{max} =-\displaystyle\frac{ R ^2}{4 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
es la la velocidad máxima del flujo ($v_{max}$) en el centro del flujo.
(ID 3627)
Ejemplos
La fuerza viscosa ($F_v$) se puede calcular a partir de las superficies paralelas ($S$), la viscosidad ($\eta$), la diferencia de velocidad entre superficies ($\Delta v$) y la distancia entre las superficies ($\Delta z$) utilizando el siguiente m todo:
| $ F_v =- S \eta \displaystyle\frac{ \Delta v }{ \Delta z }$ |
(ID 3622)
En el caso de un cilindro, la superficie est definida por ERROR:5430,0 y por el per metro de cada uno de los cilindros internos, que se calcula multiplicando $2\pi$ por el radio de la posición en un tubo ($r$). Con esto, la fuerza de resistencia en cilindro ($F_v$) se calcula utilizando la viscosidad ($\eta$) y la variación de la velocidad entre dos radios ($dv$) para el ancho del cilindro el variación del radio en un tubo ($dr$), lo que resulta en:
| $ F_v =-2 \pi r \Delta L \eta \displaystyle\frac{ dv }{ dr }$ |
(ID 3623)
Para describir el flujo, se establece un sistema de coordenadas en el cual el l quido fluye de el posición al inicio del tubo ($L_i$) a el posición al final del tubo ($L_e$), lo que implica que la presi n en la presión en la posición inicial ($p_i$) es mayor que en la presión en la posición final (e) ($p_e$). Este movimiento depender de el largo de tubo ($\Delta L$), el cual se calcula de acuerdo a:
| $ \Delta L = L_e - L_i $ |
(ID 3802)
Si se compara la viscosidad de la sangre medida con aquella estimada con la ecuaci n de Einstein se observa el siguiente comportamiento:

(ID 1694)
El primero en modelar este efecto fue Einstein (1911) que logro modelar el efecto de esferas suspendidas en un flujo sobre la viscosidad de este.
Si se aplica al caso de la sangre, donde las esferas son los hematocitos se puede estimar la viscosidad normal de la sangre
| $\eta_n=\eta_p\left(1+\displaystyle\frac{5}{2}Ht\right)$ |
La viscosidad del plasma
El modelo de Einstein es uno de cientos de modelos que existen siendo muchos espec ficos para situaciones que se dan en la sangre. Un articulo que describe distintos modelos y sirve para profundizar en el tema se puede leer en [A critical review on blood flow in large arteries; relevance to blood rheology, viscosity models, and physiologic conditions, Fuat Yalmaz and Mehmet Yasar Gundogdu, Korea-Australia Rheology Journal, Vol. 20, N0. 4, December 2008 pp. 197-211](http://downloads.gphysics.net/medicine/Yilmaz-and-Gundogdu-2008.pdf). Nota: la reolog a es la ciencia que estudia las propiedades de los materiales, en este caso los de la sangre.
(ID 3636)
Al resolver la ecuaci n de flujo con la condici n de borde, obtenemos la velocidad en un radio del cilindro ($v$) en funci n de el radio de la curvatura ($r$) como una par bola centrada en la velocidad máxima del flujo ($v_{max}$) y que se anula en el radio del tubo ($R$):
| $ v = v_{max} \left(1-\displaystyle\frac{ r ^2}{ R ^2}\right)$ |
.
(ID 3627)
El valor de la velocidad máxima del flujo ($v_{max}$) en el centro de un cilindro depende de la viscosidad ($\eta$), el radio del tubo ($R$), y del gradiente creado por la diferencia de presión ($\Delta p_s$) y el largo de tubo ($\Delta L$), como se representa a continuaci n:
| $ v_{max} =-\displaystyle\frac{ R ^2}{4 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
El signo negativo indica que el flujo siempre se produce en la direcci n negativa del gradiente, es decir, desde el rea de mayor presi n hacia el rea de menor presi n.
(ID 3628)
Cuando los gl bulos se adhieren a las paredes de los vasos tienden a enangostar el vaso. Este fen meno se denomina el efecto Fahraeus-Lindqvist y se muestra a continuaci n

Gl bulos adheridos a la pared
(ID 1896)
Esto ocurre en especial en vasos de radio menor que 0.3 mm y se denomina el efecto Fahraeus-Lindqvist. Esto se puede modelar si se asume que la capa de gl bulos en la pared reduce el radio artificialmente. La ecuaci n de flujo tendr a la forma
en donde
se tiene una viscosidad efectiva de
| $\eta_{fl}=\displaystyle\frac{\eta_n}{\left(1-\displaystyle\frac{d}{R}\right)^4}$ |
En la medida que el radio toma valores similares a la de la capa de gl bulos la viscosidad crece y el paso de sangre se dificulta.
(ID 3638)
Efecto de la deformaci n de los hematocitos
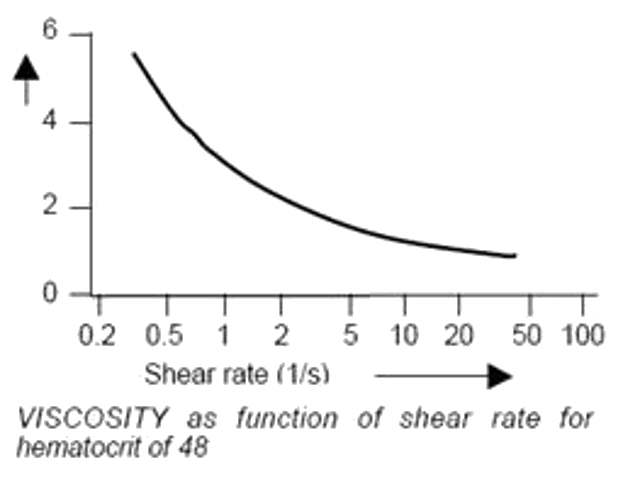
(ID 1895)
La viscosidad en estos casos baja en funci n de la velocidad con que se modifica la tensi n que se puede expresar de la forma
| $\eta_d=\displaystyle\frac{\eta_n}{1+C_{\sigma}\displaystyle\frac{d\sigma}{dt}}$ |
donde
(ID 3637)
La deformaci n de los hematocitos lleva a que se vuelven mas hidrodin micos con lo que se reduce la resistencia.

(ID 1695)
El flujo de volumen ($J_V$) se puede calcular con la ley de Hagen-Poiseuille que con los par metros la viscosidad ($\eta$), la diferencia de presión ($\Delta p$), el radio del tubo ($R$) y el largo de tubo ($\Delta L$) es:
| $ J_V =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
(ID 3178)
ID:(328, 0)
