Sistema Circulatorio
Storyboard 
El sistema circulatorio se puede modelar dentro de la hidrodinámica como un sistema de multiples bifurcaciones de capilares de distintos largos y radios. Dichos capilares poseen una resistencia hidráulica que define finalmente el flujo sanguíneo que existe.
ID:(330, 0)
Estructura de la Sangre
Definición 
Para efectos hidrodinámicos la sangre se puede describir como un fluido (el plasma) en que existen cuerpos (glóbulos) suspendidos:
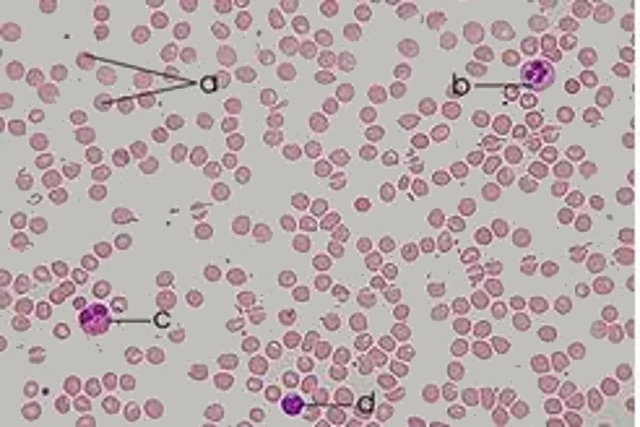
Estructura de la sangre
Los glóbulos afectan el flujo en el sentido que lo dificultan comportándose este como si fuera mas viscoso.
El plasma, que es un liquido, ocupa el 55% del volumen mientras que los restantes 45% son mayormente globulos rojos (99%, el restante 1% son loicoitos).
El plasma esta compuesto de 90% agua por lo que no es de extrañarse que la densidad de la sangre sea solo levemente superior a la del agua: $1.06 g/cm^3$
La sangre es impulsada por la presión que genera el corazón y que, en un ser humano saludable, oscila entre 60-79 mmHg (distole) y 90-119 mmHg (sístole). La unidad mmHg propviene de la forma de medir con una columna de mercurio que alcanza ante la presión de una atmósfera ($10^5,Pa$) una altura de 760 mmHg.
ID:(1894, 0)
Flujo de Líquido o Gas
Imagen 
El flujo de un liquido o gas corresponde el volumen de este que atraviesa por una sección en un tiempo dado.
Las unidades en que se mide es en unidad de volumen por unidad de tiempo como por ejemplo en metros cúbicos por segundo o litros por minuto.
ID:(9478, 0)
Velocidad media en la Sección
Nota 
Un flujo por una sección se desplaza con una velocidad que puede variar sobre esta. Sin embargo se puede definir una velocidad media simplemente considerando el flujo total por la sección.
ID:(9479, 0)
Estructura del sistema circulatorio
Cita 
La estructura del sistema circulatorio se puede describir como una serie de capilares que se van bifurcando cada vez en mas pequeños capilares (ramas arteriales) y que luego se van fusionando en cada vez mas anchas venas.
El sistema comienza con una aorta de un diámetro de
ID:(1693, 0)
Simulador de sistema circulatorio
Ejercicio 
El siguiente simulador logra modelar lo que es el flujo de sangre por el sistema circulatorio.
Las curvas finales muestran como se distribuyen a lo largo del sistema:
- los radios,
- los largos,
- el numero de vasos,
- como va cayendo la presión desde la sístole a la dístole y
- el flujo que se observa si se tiene una herida según el vaso
ID:(8018, 0)
Radio de capilares a lo largo del sistema
Ecuación 
Si se grafican los radios de los vasos en función de su posición a lo largo del sistema circulatorio se obtiene una curva del tipo

Radio de los vasos ordenados en función de su posición en el sistema.
De su valor en la aorta (12.5 mm) hasta aquel en los capilares (0.004 mm) hay una reducción en un factor en los miles (3125) que es bastante menor que aquel en el numero de vasos (de 1 a 1.2e+9). Esto se debe a que el flujo se reduce en función del radio a la cuarta por lo que debe ser compensado por un numero mucho mayor de vasos.
ID:(9472, 0)
Largo de capilares a lo largo del sistema
Script 
Si se grafican los largos de los vasos en función de su posición a lo largo del sistema circulatorio se obtiene una curva del tipo
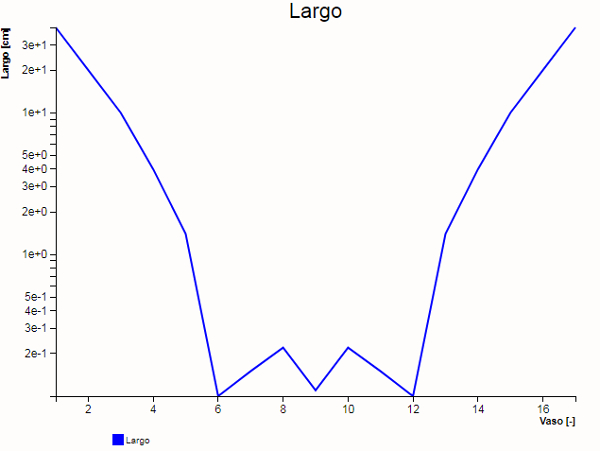
Largo de los vasos ordenados en función de su posición en el sistema.
La estructura es tal que los largos mayores en las partes extremas mientras que los largos menores se concentran en torno de los vasos menores. Esto significa que el sistema primero accesa los sistemas y luego distribuye mediante una red de vasos cortos.
ID:(9473, 0)
Numero de capilares a lo largo del sistema
Variable 
Si se grafican el numero de los vasos en función de su posición a lo largo del sistema circulatorio se obtiene una curva del tipo

Numero de los vasos ordenados en función de su posición en el sistema.
La estructura es tal que el numero menor esta en las partes extremas presentándose multiples bifurcaciones en torno de los vasos menores. Esto significa que el sistema primero accesa los sistemas y luego distribuye mediante una red de vasos cortos.
ID:(9474, 0)
Presión a lo largo del sistema
Audio 
La presión baja en forma paulatina a lo largo del sistema circulatorio siendo en la aorta mas alta (sistole) y en la vena cava mas baja (diastole). Si se va calculando la caida a lo largo del sistema se obtiene una evolución del tipo:
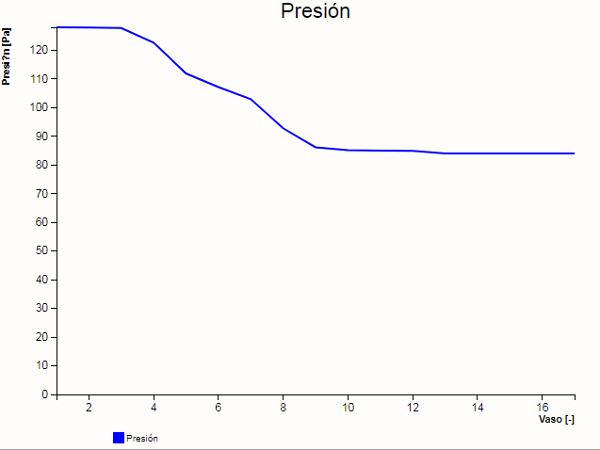
Presión en los vasos ordenados en función de su posición en el sistema.
Llama la atención que el gradiente (pendiente) es mayor en la parte inicial (aorta) y casi nula en la parte final, lo que significa que el sistema 'ayuda al corazón' apoyando la salida y reduciendo las presiones a la entrada.
ID:(9475, 0)
Velocidad a lo largo del sistema
Video 
La velocidad del flujo de sangre a lo largo del sistema circulatorio baja en forma dramática en los primeros vasos y luego se mantiene constante en torno a 2 m/s:
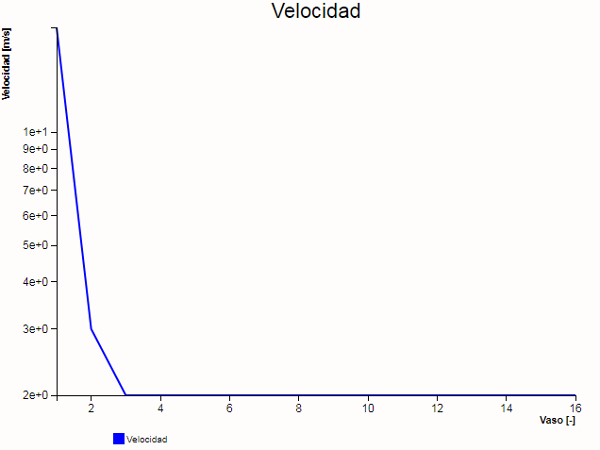
Velocidad en los vasos ordenados en función de su posición en el sistema.
Esto implica que la estructura es tal que el numero de los vasos varia en la media de los radios de estos de forma que la sección total se mantenga total.
ID:(9477, 0)
Flujos normales y con herida
Unidad 
Si se observan los flujos normales y en caso de la existencia de una herida se observa que existe una baja drástica hacia las vasos menores y de que el flujo de la herida es siempre en un factor que va de miles a decenas :
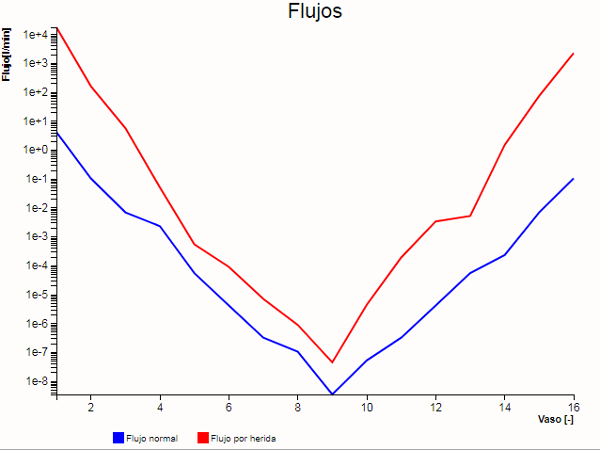
Flujos normal y en herida ordenados en función de su posición en el sistema.
Esto permite visualizar dos tipos de protecciones del organismo ante heridas. Por un lado todo lo que son vasos menores presentan flujos mínimos no peligros para el organismo. En los vasos mayores el flujo normal es mucho menor que el de la herida lo que significa que se pierde el flujo contenido en el vaso y posteriormente solo al ritmo del flujo normal que es 100 a 1000 menor.
ID:(9476, 0)
Bordes
Code 
Los bordes de los sistemas afectan el flujo desviando flujos y en caso de ser estos de mayor viscosidad reduciendo la velocidad de este en su superficie.
ID:(9482, 0)
Resistencia Hidráulica
Flujo 
La Viscosidad de un fluido lleva a que este se resista a fluir bajo una diferencia de presión. Esto ocurre en particular ante la presencia de un Bordes que lleva a que el fluido anula su velocidad sobre su superficie.
La resistencia significa perdida de energía que corresponde a la velocidad cinética que se pierde al detenerse el fluido en la superficie de los bordes del sistema.
ID:(9480, 0)
Resistencia hidráulica de elementos en serie
Matriz 
En el caso de una suma en la que los elementos están conectados en serie, la resistencia hidráulica total del sistema se calcula sumando las resistencias individuales de cada elemento.

Una forma de modelar un tubo en el que varía la sección es dividirlo en secciones de radio constante y luego sumar las resistencias hidráulicas en serie. Supongamos que tenemos una serie de la resistencia hidráulica en una red ($R_{hk}$), que depende de la viscosidad ($\eta$), el radio del cilindro k ($R_k$) y el largo de tubo k ($\Delta L_k$) a través de la siguiente ecuación:
| $ R_h =\displaystyle\frac{8 \eta | \Delta L | }{ \pi R ^4}$ |
En cada elemento habrá Una diferencia de presión en una red ($\Delta p_k$) con la resistencia hidráulica en una red ($R_{hk}$) y el flujo de volumen ($J_V$) para los que se aplica la ley de Darcy
| $ \Delta p = R_h J_V $ |
la diferencia de presión total ($\Delta p_t$) será igual a la suma de las ERROR:10132,0 individuales
| $ \Delta p_t =\displaystyle\sum_k \Delta p_k $ |
por lo que
$\Delta p_t=\displaystyle\sum_k \Delta p_k=\displaystyle\sum_k (R_{hk}J_V)=\left(\displaystyle\sum_k R_{hk}\right)J_V\equiv R_{st}J_V$
Por lo tanto, el sistema se puede modelar como un conducto único con la resistencia hidráulica calculada como la suma de las componentes individuales:
| $ R_{st} =\displaystyle\sum_k R_{hk} $ |
ID:(3630, 0)
Tubo Cilíndrico
Html 
Un tipo de Bordes es por ejemplo un tubo cilíndrico de un radio dado. Este puede ser constante o ir variando a lo largo de este.
ID:(9483, 0)
Viscosidad
Php 
La viscosidad se puede entender como la tendencia del fluido de redistribuir momento y su correspondiente velocidad.
En un liquido de alta viscosidad una zona de alta velocidad se frena por arrastrar el liquido de zonas circundante con baja velocidad que por ello gana velocidad.
En un liquido de baja viscosidad una zona de alta velocidad no es afectada mayormente por zonas de menor velocidad desplazando estas y continuando el flujo sin mayor reducción de velocidad.
ID:(9481, 0)
Conductividad hidráulica en paralelo
Iframe 
Si se tienen tres resistencias hidráulicas $R_{h1}$, $R_{h2}$ y $R_{h3}$, la suma en serie de las resistencias será:
|
|
ID:(3631, 0)
