Utilizador:
Fluxo interior e erosão
Storyboard 
O fluxo interno ocorre através dos capilares formados entre as partículas do solo. Sempre que esses capilares têm dimensões maiores do que as das pequenas placas de argila, existe o risco de que essas partículas de argila sejam arrastadas por esse fluxo. Se isso acontecer, o solo poderá perder parte de seu teor de argila, o que afetaria suas propriedades mecânicas, estabilidade e suporte para a vida orgânica.
ID:(379, 0)
Fluxo de acordo com a equação de Hagen-Poiseuille
Definição
O perfil de la velocidade em um raio do cilindro ($v$) em o raio de posição em um tubo ($r$) nos permite calcular o fluxo de volume ($J_V$) em um tubo através da integração de toda a superfície, o que nos leva à conhecida lei de Hagen-Poiseuille.
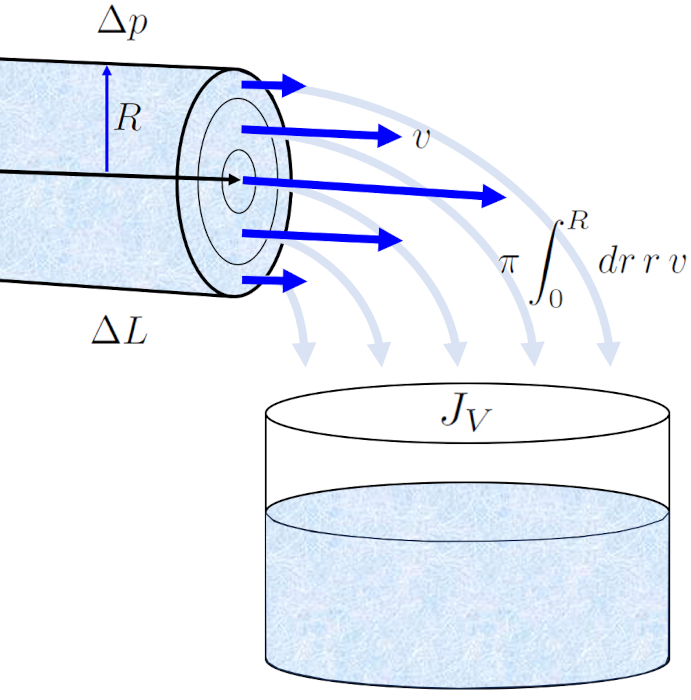
O resultado é uma equação que depende de ERROR:5417,0 elevado à quarta potência. No entanto, é fundamental observar que este perfil de fluxo só é válido no caso de um fluxo laminar.
Assim, com isso, deduz-se de la viscosidade ($\eta$) que o fluxo de volume ($J_V$) diante de um comprimento do tubo ($\Delta L$) e ERROR:6673,1, a expressão:
| $ J_V =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
Os artigos originais que deram origem a esta lei com um nome combinado foram:
"Ueber die Gesetze, welche des der Strom des Wassers in röhrenförmigen Gefässen bestimmen" (Sobre as leis que regem o fluxo da água em recipientes cilíndricos), Gotthilf Hagen, Annalen der Physik und Chemie 46:423442 (1839).
"Recherches expérimentales sur le mouvement des liquides dans les tubes de très-petits diamètres" (Pesquisa experimental sobre o movimento de líquidos em tubos de diâmetros muito pequenos), Jean-Louis-Marie Poiseuille, Comptes Rendus de l'Académie des Sciences 9:433544 (1840).
ID:(2216, 0)
Fluxo interior e erosão
Descrição
O fluxo interno ocorre através dos capilares formados entre as partículas do solo. Sempre que esses capilares têm dimensões maiores do que as das pequenas placas de argila, existe o risco de que essas partículas de argila sejam arrastadas por esse fluxo. Se isso acontecer, o solo poderá perder parte de seu teor de argila, o que afetaria suas propriedades mecânicas, estabilidade e suporte para a vida orgânica.
Variáveis
Cálculos
para 
,
depois, selecione a variável: 
para 
Cálculos
Variáve
Dado
Calcular
Objetivo :
Equação
A ser usado
Equações
Outra equa o til aquela que corresponde conserva o de energia, a qual aplic vel em casos em que a viscosidade, um processo que resulta em perda de energia, pode ser negligenciada. Se considerarmos a equa o cl ssica da energia $E$, que leva em conta a energia cin tica, a energia potencial gravitacional e uma for a externa que desloca o l quido por uma dist ncia $\Delta z$, podemos express -la da seguinte forma:
$E=\displaystyle\frac{m}{2}v^2+mgh+F\Delta x$
Se considerarmos a energia em um volume $\Delta x\Delta y\Delta z$, podemos substituir a massa por:
$m=\rho \Delta x\Delta y\Delta z$
E como a press o dada por:
$F=p \Delta S =p \Delta y\Delta z$
Obtemos a equa o para a densidade de energia:
| $ e =\displaystyle\frac{1}{2} \rho v ^2+ \rho g h + p $ |
(ID 3159)
Quando uma la diferença de pressão ($\Delta p_s$) age sobre uma se o com uma rea de $\pi R^2$, com o raio do tubo ($R$) como o raio de curvatura ($r$), ela gera uma for a representada por:
$\pi r^2 \Delta p$
Essa for a impulsiona o l quido contra a resist ncia viscosa, dada por:
Ao igualarmos essas duas for as, obtemos:
$\pi r^2 \Delta p = \eta 2\pi r \Delta L \displaystyle\frac{dv}{dr}$
O que nos leva equa o:
$\displaystyle\frac{dv}{dr} = \displaystyle\frac{1}{2\eta}\displaystyle\frac{\Delta p}{\Delta L} r$
Se integrarmos essa equa o de uma posi o definida por o raio de curvatura ($r$) at a borda onde o raio do tubo ($R$) est (levando em considera o que a velocidade na borda zero), podemos obter la velocidade em um raio do cilindro ($v$) como fun o de o raio de curvatura ($r$):
Onde:
la taxa de fluxo máxima ($v_{max}$) no centro do fluxo.
(ID 3627)
Se assumirmos que la densidade de energia ($e$) conservado, podemos afirmar que para uma c lula onde a velocidade m dia la velocidade em um raio do cilindro ($v$), a densidade la densidade ($\rho$), a press o la pressão da coluna de água ($p$), a altura la altura da coluna ($h$) e a acelera o gravitacional la aceleração gravitacional ($g$), temos o seguinte:
| $ e =\displaystyle\frac{1}{2} \rho v ^2+ \rho g h + p $ |
Em um ponto 1, essa equa o ser igual mesma equa o em um ponto 2:
$e(v_1,p_1,h_1)=e(v_2,p_2,h_2)$
onde la velocidade média do fluido no ponto 1 ($v_1$), la hauteur ou profondeur 1 ($h_1$) e la pressão na coluna 1 ($p_1$) representam a velocidade, altura e press o no ponto 1, respectivamente, e la velocidade média do fluido no ponto 2 ($v_2$), la hauteur ou profondeur 2 ($h_2$) e la pressão na coluna 2 ($p_2$) representam a velocidade, altura e press o no ponto 2, respectivamente. Portanto, temos:
| $\displaystyle\frac{1}{2} \rho v_1 ^2+ \rho g h_1 + p_1 =\displaystyle\frac{1}{2} \rho v_2 ^2+ \rho g h_2 + p_2 $ |
(ID 4504)
No caso em que n o h press o hisstrost tica, aplica-se a lei de Bernoulli para la densidade ($\rho$), la pressão na coluna 1 ($p_1$), la pressão na coluna 2 ($p_2$), la velocidade média do fluido no ponto 1 ($v_1$) e < var>5416
| $\displaystyle\frac{1}{2} \rho v_1 ^2 + p_1 =\displaystyle\frac{1}{2} \rho v_2 ^2 + p_2 $ |
pode ser reescrito com ERROR:6673
| $ dp = p - p_0 $ |
e tendo em mente que
$v_2^2 - v_1^2 = \displaystyle\frac{1}{2}(v_2-v_1)(v_1+v_2)$
com
| $ \bar{v} = \displaystyle\frac{ v_1 + v_2 }{2}$ |
e
| $ \Delta v = v_2 - v_1 $ |
se tem que
| $ \Delta p = - \rho \bar{v} \Delta v $ |
(ID 4835)
Exemplos
Uma vez que um fluido ou g s um cont nuo, o conceito de energia j n o pode ser associado a uma massa espec fica. No entanto, poss vel considerar a energia contida num volume do cont nuo e, ao dividir pela pr pria volume, obtemos la densidade de energia ($e$). Portanto, com la densidade ($\rho$), la velocidade em um raio do cilindro ($v$), la altura da coluna ($h$), la aceleração gravitacional ($g$) e la pressão da coluna de água ($p$), temos:
| $ e =\displaystyle\frac{1}{2} \rho v ^2+ \rho g h + p $ |
o que corresponde equa o de Bernoulli.
(ID 3159)
Com la velocidade média do fluido no ponto 1 ($v_1$), la hauteur ou profondeur 1 ($h_1$) e la pressão na coluna 1 ($p_1$) representando a velocidade, altura e press o no ponto 1, respectivamente, e la velocidade média do fluido no ponto 2 ($v_2$), la hauteur ou profondeur 2 ($h_2$) e la pressão na coluna 2 ($p_2$) representando a velocidade, altura e press o no ponto 2, respectivamente, temos:
| $\displaystyle\frac{1}{2} \rho v_1 ^2+ \rho g h_1 + p_1 =\displaystyle\frac{1}{2} \rho v_2 ^2+ \rho g h_2 + p_2 $ |
(ID 4504)
ERROR:6673 pode ser calculado a partir de la velocidade média ($\bar{v}$) e la diferença de velocidade entre superfícies ($\Delta v$) com la densidade ($\rho$) usando
| $ \Delta p = - \rho \bar{v} \Delta v $ |
o que nos permite ver o efeito da velocidade m dia de um corpo e a diferen a entre suas superf cies, como observado na asa de um avi o ou de um p ssaro.
(ID 4835)
O perfil de la velocidade em um raio do cilindro ($v$) em o raio de posição em um tubo ($r$) nos permite calcular o fluxo de volume ($J_V$) em um tubo atrav s da integra o de toda a superf cie, o que nos leva conhecida lei de Hagen-Poiseuille.
O resultado uma equa o que depende de ERROR:5417,0 elevado quarta pot ncia. No entanto, fundamental observar que este perfil de fluxo s v lido no caso de um fluxo laminar.
Assim, com isso, deduz-se de la viscosidade ($\eta$) que o fluxo de volume ($J_V$) diante de um comprimento do tubo ($\Delta L$) e ERROR:6673,1, a express o:
| $ J_V =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
Os artigos originais que deram origem a esta lei com um nome combinado foram:
"Ueber die Gesetze, welche des der Strom des Wassers in r hrenf rmigen Gef ssen bestimmen" (Sobre as leis que regem o fluxo da gua em recipientes cil ndricos), Gotthilf Hagen, Annalen der Physik und Chemie 46:423442 (1839).
"Recherches exp rimentales sur le mouvement des liquides dans les tubes de tr s-petits diam tres" (Pesquisa experimental sobre o movimento de l quidos em tubos de di metros muito pequenos), Jean-Louis-Marie Poiseuille, Comptes Rendus de l'Acad mie des Sciences 9:433544 (1840).
(ID 2216)
Ao resolver a equa o de fluxo com a condi o de contorno, obtemos la velocidade em um raio do cilindro ($v$) como uma fun o de o raio de curvatura ($r$), representada por uma par bola centrada em la taxa de fluxo máxima ($v_{max}$) e igual a zero em o raio do tubo ($R$):
| $ v = v_{max} \left(1-\displaystyle\frac{ r ^2}{ R ^2}\right)$ |
.
(ID 3627)
O valor de la taxa de fluxo máxima ($v_{max}$) no centro de um cilindro depende de la viscosidade ($\eta$), o raio do tubo ($R$) e do gradiente criado por la diferença de pressão ($\Delta p_s$) e o comprimento do tubo ($\Delta L$), conforme representado abaixo:
| $ v_{max} =-\displaystyle\frac{ R ^2}{4 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
O sinal negativo indica que o fluxo sempre ocorre na dire o oposta ao gradiente, ou seja, da rea de maior press o para a rea de menor press o.
(ID 3628)
ID:(379, 0)