Usuario:
Flujo interior y erosión
Storyboard 
El flujo interior se produce a través de los capilares que se forman entre los granos. Cada vez que estos capilares tienen dimensiones mayores que las de las pequeñas placas de arcilla, existe el riesgo de que estas últimas sean arrastradas por dicho flujo. Si esto sucede, el suelo podría perder parte de su contenido de arcilla, lo que afectaría sus propiedades mecánicas, estabilidad y capacidad de soporte para la vida orgánica.
ID:(379, 0)
Flujo en suelo y efecto en plaquitas
Descripción
La erosión puede remover parte de las componentes del suelo reduciendo la superficie interna sobre la que se basa el desarrollo vegetal.
ID:(18, 0)
Corriente en porosidad
Descripción
La porosidad permite el desplazamiento de agua creando corrientes en el suelo.Dichas corrientes puede arrastra consigo las plaquitas de las que esta compuesta la arcilla. Esto tanto por su menor masa como por su forma mas aerodinámica.La remoción de las plaquitas es grave ya que reduce en forma sustancial la cantidad de superficie que contiene el suelo con lo que se afecta en forma directa la capacidad del suelo de soportar vida.El transporte de materiales como la arcilla dependen de la velocidad del fluido. Esta depende a su vez del gradiente de presión y del nivel de compactación del material. Por ello el empobrecimiento del suelo es una función de las características de este y de las condiciones bajo las cuales fluye el agua por la porosidad existente.Para comprender como levitan las plaquitas debemos estudiar la corriente que se da en su entorno.
ID:(1237, 0)
Perfil de velocidad del flujo en el suelo
Descripción
Si se asume que los capilares del suelo se pueden modelar como cilindros, el perfil de velocidades tendrá la forma:
| $ v = v_{max} \left(1-\displaystyle\frac{ r ^2}{ R ^2}\right)$ |
donde
La velocidad máxima es igual a
| $ v_{max} =-\displaystyle\frac{ R ^2}{4 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
donde
ID:(107, 0)
Flujo según ecuación de Hagen-Poiseuille
Concepto
El perfil de la velocidad en un radio del cilindro ($v$) en el radio de la posición en un tubo ($r$) permite calcular el flujo de volumen ($J_V$) en un tubo mediante una integración de toda la superficie, lo que nos conduce a la conocida ley de Hagen-Poiseuille.
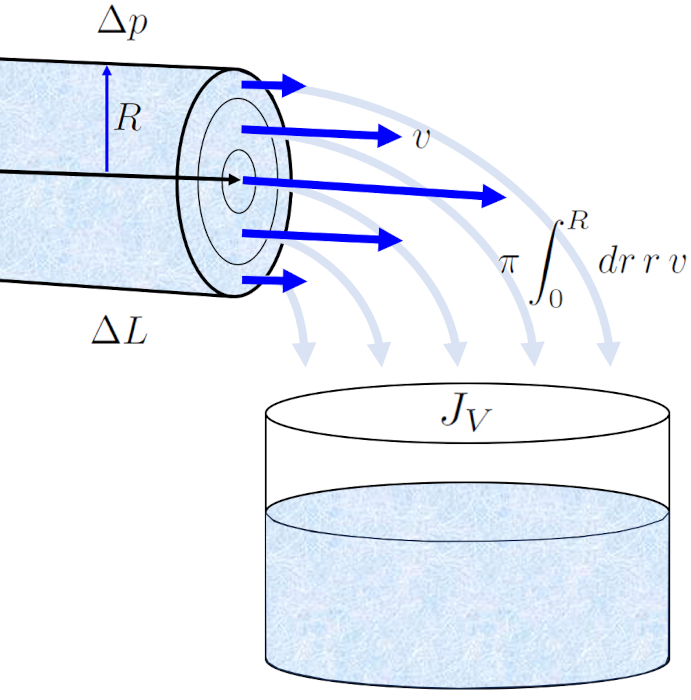
El resultado es una ecuación que depende de ERROR:5417,0 elevado a la cuarta potencia. No obstante, es fundamental tener en cuenta que este perfil de flujo solo se mantiene en caso de que el flujo sea laminar.
Con ello, se deduce de la viscosidad ($\eta$) que el flujo de volumen ($J_V$) ante un largo de tubo ($\Delta L$) y un diferencial de la presión ($\Delta p$) la expresión:
| $ J_V =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
Los articulos originales que dieron origen a esta ley con un nombre combinado fueron:
"Ueber die Gesetze, welche des der Strom des Wassers in röhrenförmigen Gefässen bestimmen" (Sobre las leyes que rigen el flujo del agua en recipientes cilíndricos), Gotthilf Hagen, Annalen der Physik und Chemie 46:423442 (1839) "Recherches expérimentales sur le mouvement des liquides dans les tubes de très-petits diamètres" (Investigación experimental sobre el movimiento de líquidos en tubos de diámetros muy pequeños), Jean-Louis-Marie Poiseuille, Comptes Rendus de l'Académie des Sciences 9:433544 (1840).
ID:(2216, 0)
Fuerzas sobre plaquitas
Imagen
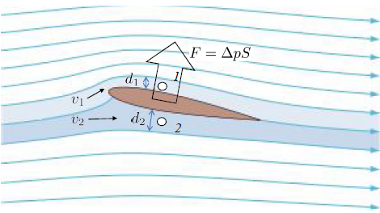
Si una plaquita de arcilla se encuentra en el fondo de un caudal se genera una diferencia de presión entre la parte superior y la inferior que genera una fuerza efectiva que intenta elevarla hacia el caudal.
ID:(1639, 0)
Flujo interior y erosión
Modelo
El flujo interior se produce a través de los capilares que se forman entre los granos. Cada vez que estos capilares tienen dimensiones mayores que las de las pequeñas placas de arcilla, existe el riesgo de que estas últimas sean arrastradas por dicho flujo. Si esto sucede, el suelo podría perder parte de su contenido de arcilla, lo que afectaría sus propiedades mecánicas, estabilidad y capacidad de soporte para la vida orgánica.
Variables
Cálculos
a 
,
luego, seleccione la variable: 
a 
Cálculos
Variable
Dado
Calcule
Objetivo :
Ecuación
A utilizar
Ecuaciones
Otra ecuaci n til es la que corresponde a la conservaci n de energ a, que se aplica en casos donde la viscosidad, un proceso en el cual se pierde energ a, puede ser despreciada. Si consideramos la cl sica ecuaci n de energ a $E$, que incluye la energ a cin tica, la energ a potencial gravitacional y una fuerza externa que desplaza el l quido una distancia $\Delta z$, podemos expresarla de la siguiente manera:
$E=\displaystyle\frac{m}{2}v^2+mgh+F\Delta x$
Si consideramos la energ a en un volumen $\Delta x\Delta y\Delta z$, podemos reemplazar la masa por:
$m=\rho \Delta x\Delta y\Delta z$
Y como la presi n se expresa como:
$F=p \Delta S =p \Delta y\Delta z$
Obtenemos la ecuaci n de densidad de energ a:
| $ e =\displaystyle\frac{1}{2} \rho v ^2+ \rho g h + p $ |
(ID 3159)
La diferencia de presión ($\Delta p_s$) sobre una secci n de rea $\pi R^2$, con el radio del tubo ($R$) como el radio de la curvatura ($r$), genera una fuerza que se representa como:
$\pi r^2 \Delta p$
Esta fuerza impulsa el l quido en contra de la resistencia viscosa, que est dada por:
| $ F_v =-2 \pi r \Delta L \eta \displaystyle\frac{ dv }{ dr }$ |
Igualando estas dos fuerzas, obtenemos:
$\pi r^2 \Delta p = \eta 2\pi r \Delta L \displaystyle\frac{dv}{dr}$
Lo que nos lleva a la ecuaci n:
$\displaystyle\frac{dv}{dr} = \displaystyle\frac{1}{2\eta}\displaystyle\frac{\Delta p}{\Delta L} r$
Si integramos esta ecuaci n desde una posici n definida por el radio de la curvatura ($r$) hasta el borde donde el radio del tubo ($R$) (teniendo en cuenta que la velocidad en el borde es nula), podemos obtener la velocidad en un radio del cilindro ($v$) en funci n de el radio de la curvatura ($r$):
| $ v = v_{max} \left(1-\displaystyle\frac{ r ^2}{ R ^2}\right)$ |
Donde:
| $ v_{max} =-\displaystyle\frac{ R ^2}{4 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
es la la velocidad máxima del flujo ($v_{max}$) en el centro del flujo.
(ID 3627)
Si asumimos que la densidad de energía ($e$) se conserva, podemos afirmar que para una celda en la que la velocidad media es la velocidad en un radio del cilindro ($v$), la densidad es la densidad ($\rho$), la presi n es la presión de la columna de agua ($p$), la altura es la altura de la columna ($h$) y la aceleraci n gravitacional es la aceleración gravitacional ($g$), se cumple lo siguiente:
| $ e =\displaystyle\frac{1}{2} \rho v ^2+ \rho g h + p $ |
En un punto 1, esta ecuaci n ser igual a la misma ecuaci n en un punto 2:
$e(v_1,p_1,h_1)=e(v_2,p_2,h_2)$
con la velocidad media del fluido en el punto 1 ($v_1$), la altura o profundidad 1 ($h_1$) y la presión en la columna 1 ($p_1$) representan la velocidad, altura y presi n en el punto 1, respectivamente, y la velocidad media del fluido en el punto 2 ($v_2$), la altura o profundidad 2 ($h_2$) y la presión en la columna 2 ($p_2$) representan la velocidad, altura y presi n en el punto 2, respectivamente. Por lo tanto, se tiene:
| $\displaystyle\frac{1}{2} \rho v_1 ^2+ \rho g h_1 + p_1 =\displaystyle\frac{1}{2} \rho v_2 ^2+ \rho g h_2 + p_2 $ |
(ID 4504)
(ID 4506)
(ID 4507)
Para el caso de que no exista presi n histrostatica la ley de Bernoulli para la densidad ($\rho$), la presión en la columna 1 ($p_1$), la presión en la columna 2 ($p_2$), la velocidad media del fluido en el punto 1 ($v_1$) y la velocidad media del fluido en el punto 2 ($v_2$)
| $\displaystyle\frac{1}{2} \rho v_1 ^2 + p_1 =\displaystyle\frac{1}{2} \rho v_2 ^2 + p_2 $ |
se puede reescribir con el diferencial de la presión ($\Delta p$)
| $ dp = p - p_0 $ |
y teniendo presente de que
$v_2^2 - v_1^2 = \displaystyle\frac{1}{2}(v_2-v_1)(v_1+v_2)$
con
| $ \bar{v} = \displaystyle\frac{ v_1 + v_2 }{2}$ |
y
| $ \Delta v = v_2 - v_1 $ |
se tiene que
| $ \Delta p = - \rho \bar{v} \Delta v $ |
(ID 4835)
(ID 10630)
Ejemplos
La erosi n puede remover parte de las componentes del suelo reduciendo la superficie interna sobre la que se basa el desarrollo vegetal.
(ID 18)
La porosidad permite el desplazamiento de agua creando corrientes en el suelo.Dichas corrientes puede arrastra consigo las plaquitas de las que esta compuesta la arcilla. Esto tanto por su menor masa como por su forma mas aerodin mica.La remoci n de las plaquitas es grave ya que reduce en forma sustancial la cantidad de superficie que contiene el suelo con lo que se afecta en forma directa la capacidad del suelo de soportar vida.El transporte de materiales como la arcilla dependen de la velocidad del fluido. Esta depende a su vez del gradiente de presi n y del nivel de compactaci n del material. Por ello el empobrecimiento del suelo es una funci n de las caracter sticas de este y de las condiciones bajo las cuales fluye el agua por la porosidad existente.Para comprender como levitan las plaquitas debemos estudiar la corriente que se da en su entorno.
(ID 1237)
Si se asume que los capilares del suelo se pueden modelar como cilindros, el perfil de velocidades tendr la forma:
| $ v = v_{max} \left(1-\displaystyle\frac{ r ^2}{ R ^2}\right)$ |
donde
La velocidad m xima es igual a
| $ v_{max} =-\displaystyle\frac{ R ^2}{4 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
donde
(ID 107)
El perfil de la velocidad en un radio del cilindro ($v$) en el radio de la posición en un tubo ($r$) permite calcular el flujo de volumen ($J_V$) en un tubo mediante una integraci n de toda la superficie, lo que nos conduce a la conocida ley de Hagen-Poiseuille.
El resultado es una ecuaci n que depende de ERROR:5417,0 elevado a la cuarta potencia. No obstante, es fundamental tener en cuenta que este perfil de flujo solo se mantiene en caso de que el flujo sea laminar.
Con ello, se deduce de la viscosidad ($\eta$) que el flujo de volumen ($J_V$) ante un largo de tubo ($\Delta L$) y un diferencial de la presión ($\Delta p$) la expresi n:
| $ J_V =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
Los articulos originales que dieron origen a esta ley con un nombre combinado fueron: "Ueber die Gesetze, welche des der Strom des Wassers in r hrenf rmigen Gef ssen bestimmen" (Sobre las leyes que rigen el flujo del agua en recipientes cil ndricos), Gotthilf Hagen, Annalen der Physik und Chemie 46:423442 (1839) "Recherches exp rimentales sur le mouvement des liquides dans les tubes de tr s-petits diam tres" (Investigaci n experimental sobre el movimiento de l quidos en tubos de di metros muy peque os), Jean-Louis-Marie Poiseuille, Comptes Rendus de l'Acad mie des Sciences 9:433544 (1840).
(ID 2216)
Si una plaquita de arcilla se encuentra en el fondo de un caudal se genera una diferencia de presi n entre la parte superior y la inferior que genera una fuerza efectiva que intenta elevarla hacia el caudal.
(ID 1639)
ID:(379, 0)