Storyboard

Le flux interne se produit à travers les capillaires formés entre les particules du sol. Chaque fois que ces capillaires ont des dimensions plus grandes que celles des petites plaques d'argile, il y a un risque que ces particules d'argile soient emportées par ce flux. Si cela se produit, le sol pourrait perdre une partie de sa teneur en argile, ce qui aurait un impact sur ses propriétés mécaniques, sa stabilité et son soutien à la vie organique.

>Modèle

ID:(379, 0)

Équation

>Top, >Modèle

Étant donné qu'un fluide ou un gaz est un continuum, le concept d'énergie ne peut plus être associé à une masse spécifique. Cependant, il est possible de considérer l'énergie contenue dans un volume du continuum, et en la divisant par le volume lui-même, nous obtenons a densité d'énergie ($e$). Par conséquent, avec a densité ($\rho$), a vitesse dans un rayon du cylindre ($v$), a hauteur de la colonne ($h$), a accélération gravitationnelle ($g$) et a pression de la colonne d'eau ($p_t$), nous avons :

$ e =\displaystyle\frac{1}{2} \rho v ^2+ \rho g h + p $

Conditions

Variables

$g$

Accélération gravitationnelle

9.8

$m/s^2$

$\rho$

Densité

$kg/m^3$

$e$

Densité d'énergie

$J/m^3$

$h$

Hauteur de la colonne

$m$

$p$

Pression de la colonne d'eau

$Pa$

$v$

Vitesse dans un rayon du cylindre

$m/s$

Relation

Développement

Une autre équation utile est celle correspondant à la conservation de l'énergie, qui s'applique dans les cas où la viscosité, un processus entraînant une perte d'énergie, peut être négligée. Si l'on considère l\'équation classique de l'énergie $E$, qui prend en compte l\'énergie cinétique, l\'énergie potentielle gravitationnelle et une force externe déplaçant le liquide sur une distance $\Delta z$, on peut l\'exprimer de la manière suivante :

$E=\displaystyle\frac{m}{2}v^2+mgh+F\Delta x$

Si l\'on considère l\'énergie à l\'intérieur d\'un volume $\Delta x\Delta y\Delta z$, on peut remplacer la masse par :

$m=\rho \Delta x\Delta y\Delta z$

Et puisque la pression est donnée par :

$F=p \Delta S =p \Delta y\Delta z$

On obtient l\'équation de la densité d\'énergie :

$ e =\displaystyle\frac{1}{2} \rho v ^2+ \rho g h + p $

qui correspond à l'équation de Bernoulli.

En l'absence de viscosité, la conservation de l'énergie implique que a densité d'énergie ($e$) soit constant à n'importe quel point du fluide. Par conséquent, connaître la vitesse et/ou la pression en tout endroit du fluide est suffisant pour établir une relation entre la vitesse et la pression en tout point du fluide.

ID:(3159, 0)

Équation

>Top, >Modèle

Si l'énergie est conservée et que le milieu s'écoule sans se déformer, la densité entre deux points doit être égale, ce qui conduit à l\'équation bien connue de Bernoulli :

$\displaystyle\frac{1}{2} \rho v_1 ^2+ \rho g h_1 + p_1 =\displaystyle\frac{1}{2} \rho v_2 ^2+ \rho g h_2 + p_2 $

Conditions

Variables

$g$

Accélération gravitationnelle

9.8

$m/s^2$

$\rho$

Densité du liquide

$kg/m^3$

$h_1$

Hauteur ou profondeur 1

$m$

$h_2$

Hauteur ou profondeur 2

$m$

$p_1$

Pression dans la colonne 1

$Pa$

$p_2$

Pression dans la colonne 2

$Pa$

$v_1$

Vitesse moyenne du fluide au point 1

$m/s$

$v_2$

Vitesse moyenne du fluide au point 2

$m/s$

Relation

Développement

Si l'on suppose que la densité d'énergie est conservée, pour une cellule dans laquelle la vitesse moyenne est v, la densité est \rho, la pression est p, la hauteur est h et l\'accélération gravitationnelle est g, on a :



Au point 1, cette équation sera égale à la même équation au point 2 :

$e(v_1,p_1,h_1)=e(v_2,p_2,h_2)$

où v_1, h_1 et p_1 représentent respectivement la vitesse, la hauteur et la pression au point 1, et v_2, h_2 et p_2 représentent respectivement la vitesse, la hauteur et la pression au point 2. Ainsi, on a :

Il est important de garder à l\'esprit les hypothèses suivantes :

L\'énergie est conservée, en supposant notamment l\'absence de viscosité.

Il n\'y a pas de déformation du milieu, donc la densité reste constante.

Il n\'y a pas de vorticité, c\'est-à-dire de tourbillons qui entraînent une circulation dans le milieu. Le fluide doit présenter un comportement laminaire.

ID:(4504, 0)

Équation

>Top, >Modèle

($$) peut être calculé à partir de a vitesse moyenne ($\bar{v}$) et a différence de vitesse entre les surfaces ($\Delta v$) avec a densité ($\rho$) en utilisant

$ \Delta p = - \rho \bar{v} \Delta v $

Conditions

Variables

$\rho$

Densité

$kg/m^3$

$\Delta v$

Différence de vitesse entre les surfaces

$m/s$

$\bar{v}$

Vitesse moyenne

$m/s$

Relation

Développement

Dans le cas où il n'y a pas de pression hystrostatique, la loi de Bernoulli pour a densité du liquide ($\rho_w$), a pression dans la colonne 1 ($p_1$), a pression dans la colonne 2 ($p_2$), a vitesse moyenne du fluide au point 1 ($v_1$) et < var>5416



peut être réécrit avec ($$)



et en gardant à l'esprit que

$v_2^2 - v_1^2 = \displaystyle\frac{1}{2}(v_2-v_1)(v_1+v_2)$

avec



et



il faut que

ce qui nous permet de voir l'effet de la vitesse moyenne d'un corps et de la différence entre ses surfaces, comme observé dans une aile d'avion ou d'oiseau.

ID:(4835, 0)

Concept

>Top

Le profil de a vitesse dans un rayon du cylindre ($v$) en le rayon de position dans un tube ($r$) nous permet de calculer le volumique flux ($J_V$) dans un tube en intégrant sur toute la surface, ce qui nous conduit à la loi bien connue de Hagen-Poiseuille.

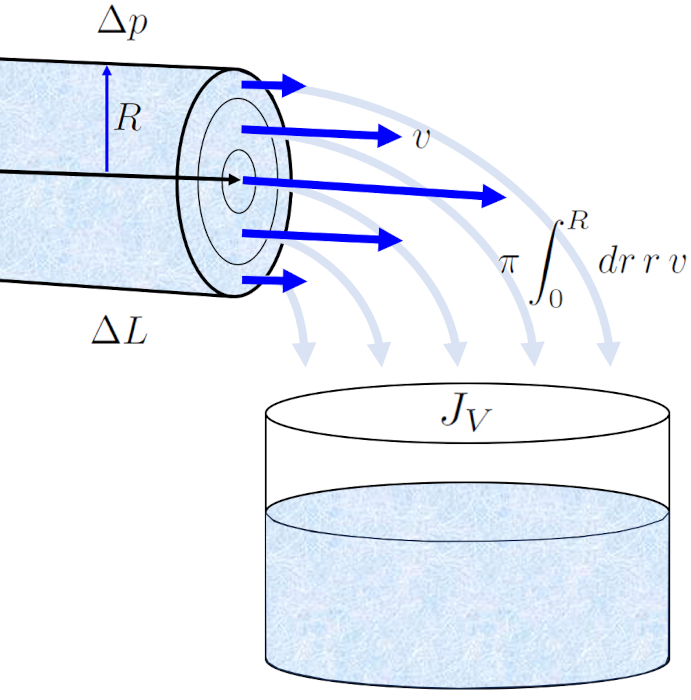
Le résultat est une équation qui dépend de rayon du cylindre ($R$) élevé à la quatrième puissance. Cependant, il est essentiel de noter que ce profil d'écoulement n'est valable que dans le cas d'un écoulement laminaire.

Ainsi, avec cela, on déduit de a viscosité ($\eta$) que le volumique flux ($J_V$) devant un longueur du tube ($\Delta L$) et ($$), l'expression :

ID:(2216, 0)

Équation

>Top, >Modèle

En résolvant l'équation de flux avec la condition aux limites, nous obtenons a vitesse dans un rayon du cylindre ($v$) comme une fonction de le rayon de courbure ($r$), représentée par une parabole centrée sur a vitesse maximal ($v_{max}$) et égale à zéro en le rayon du cylindre ($R$) :

$ v = v_{max} \left(1-\displaystyle\frac{ r ^2}{ R ^2}\right)$

Conditions

Variables

$r$

Position radiale dans le cylindre

$m$

$R$

Rayon du cylindre

$m$

$v$

Vitesse dans un rayon du cylindre

$m/s$

$v_{max}$

Vitesse maximal

$m/s$

Relation

Développement

Quand une a différence de pression ($\Delta p$) agit sur une section avec une aire de $\pi R^2$, avec le rayon du cylindre ($R$) comme le rayon de courbure ($r$), elle génère une force représentée par :

$\pi r^2 \Delta p$

Cette force pousse le liquide contre la résistance visqueuse, donnée par :



En égalant ces deux forces, nous obtenons :

$\pi r^2 \Delta p = \eta 2\pi r \Delta L \displaystyle\frac{dv}{dr}$

Ce qui nous conduit à l'équation :

$\displaystyle\frac{dv}{dr} = \displaystyle\frac{1}{2\eta}\displaystyle\frac{\Delta p}{\Delta L} r$

Si nous intégrons cette équation d'une position définie par le rayon de courbure ($r$) jusqu'au bord où se trouve le rayon du cylindre ($R$) (en tenant compte que la vitesse au bord est nulle), nous pouvons obtenir a vitesse dans un rayon du cylindre ($v$) en fonction de le rayon de courbure ($r$) :



Où :



est a vitesse maximal ($v_{max}$) au centre de l'écoulement.

.

ID:(3627, 0)

Équation

>Top, >Modèle

La valeur de a vitesse maximal ($v_{max}$) au centre d'un cylindre dépend de a viscosité ($\eta$), le rayon du cylindre ($R$) et du gradient créé par a différence de pression ($\Delta p$) et le longueur du tube ($\Delta L$), comme représenté ci-dessous :

$ v_{max} =-\displaystyle\frac{ R ^2}{4 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$

Conditions

Variables

$\Delta L$

Longueur du tube

$m$

$R$

Rayon du cylindre

$m$

$\eta$

Viscosité

$Pa s$

$v_{max}$

Vitesse maximal

$m/s$

Relation

Le signe négatif indique que le flux s'effectue toujours dans la direction opposée au gradient, c'est-à-dire, de la zone de plus haute pression vers la zone de plus basse pression.

ID:(3628, 0)