Usuario:
Mortalidad específica con malaria
Imagen
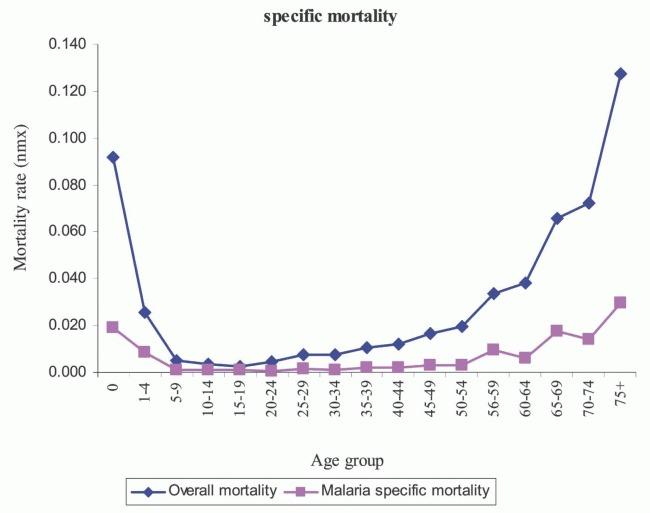
La mortalidad específica de una persona con malaria muestra que es una enfermedad que ataca ante todo a niños y ancianos. La gráfica adjunta, del estudio ['How Many Years of Life Could Be Saved If Malaria Were Eliminated from a Hyperendemic Area of Northern Ghana?'](http://www.gphysics.net/downloads/medicine/Bookshelf_NBK1712.pdf) de Ayaga A. Bawah and Fred N. Binka muestra la mortalidad según edad con y sin malaria:
ID:(8215, 0)
Expectativa de vida con malaria
Imagen
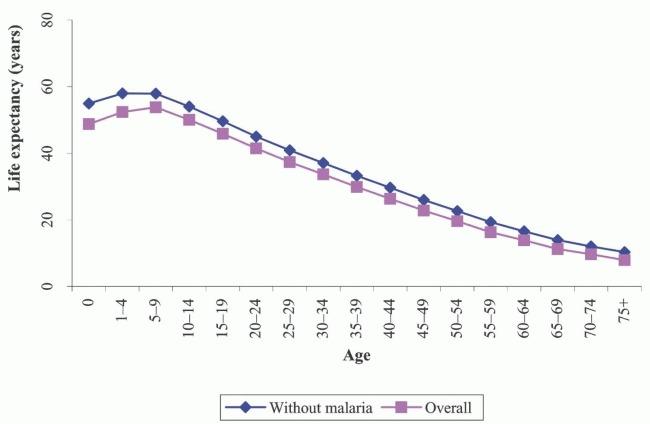
La expectativa de vida promedio de una persona con malaria se reduce en promedio en aproximadamente 10 años. La gráfica adjunta, del estudio ['How Many Years of Life Could Be Saved If Malaria Were Eliminated from a Hyperendemic Area of Northern Ghana?'](http://www.gphysics.net/downloads/medicine/Bookshelf_NBK1712.pdf) de Ayaga A. Bawah and Fred N. Binka muestra la expectativa de vida según edad con y sin malaria:
ID:(8214, 0)
Estadística de poblaciones de mosquitos y picaduras
Imagen
En el articulo ['Human-to-mosquito transmission effciency increases as malaria is controlled'](http://www.gphysics.net/downloads/medicine/Churcher_et_al-2015-Nature_Communications.pdf) de Thomas S. Churcher, Jean-Francois Trape y Anna Cohuet en Nature Communications publicado el 19 de enero del 2015 se observan las curvas que se ven en la imagen a continuación:
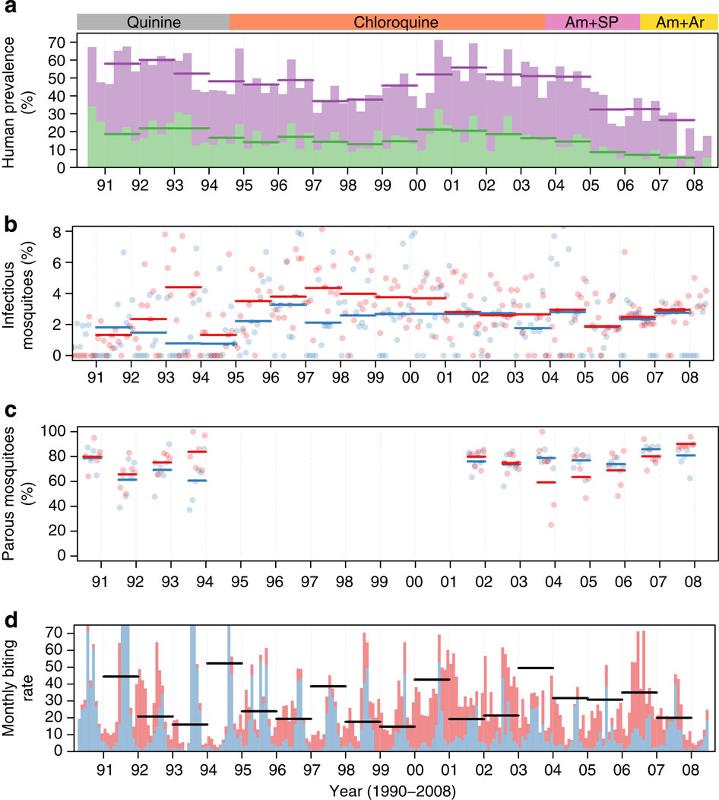
Rescatamos que la fracción de mosquitos
Por otro lado se observan alrededor de 30 picadas al mes. Por ello la probabilidad de picadura diaria
Si se piensa en medidas se pueden estudiar los años en que el numero de picaduras retrocedio y determinar la causa de esto. A modo de ejemplo, si se detectara que en año de sequía baja la tasa se podría concluir que con medidas de drenaje se pueden secar zonas propensas a habitar mosquitos con malaria. En dicho caso se pueden tomar los datos de dichos años favorables para determinar un set de datos que se darían para el caso de tomar medidas. Es asi como una baja de 30 a 15 picaduras por mes llevaría a que con medidas la probabilidad de ser picado
Nota: Es importante tener presente que el factor
ID:(8199, 0)
Estimación de probabilidades de contagio de humanos
Ecuación
Si se conoce la situación asintótica de una población de humanos con malaria se pueden empelar las ecuaciones
| $i_{\infty}=\displaystyle\frac{\Lambda p_b^2p_Ip_V-\mu\gamma}{p_bp_V(\gamma+\Lambda p_bp_I)}$ |
y
| $v_{\infty}=\displaystyle\frac{\Lambda p_b^2p_Ip_V-\mu\gamma}{\Lambda p_bp_I(\mu+p_bp_V)}$ |
para determinar
| $p_i=\displaystyle\frac{\gamma i}{(1-i)p_b v \Lambda}$ |
ID:(8211, 0)
Estimación de probabilidades de contagio de mosquito
Ecuación
Si se conoce la situación asintotica de una población de humanos con malaria se pueden empelar las ecuaciones
| $i_{\infty}=\displaystyle\frac{\Lambda p_b^2p_Ip_V-\mu\gamma}{p_bp_V(\gamma+\Lambda p_bp_I)}$ |
y
| $v_{\infty}=\displaystyle\frac{\Lambda p_b^2p_Ip_V-\mu\gamma}{\Lambda p_bp_I(\mu+p_bp_V)}$ |
para determinar
| $p_v=\displaystyle\frac{\mu v}{p_b i(1-v)}$ |
ID:(8212, 0)
Estadística país
Descripción
Población:
Año | Enfermos | Muertes
:-----:|:-------:|:---------:
2000 | 3349528 | 6108 |
2001 | 3044844 | 1717 |
2002 | 3140893 | 2376 |
2003 | 3552896 | 2103 |
2004 | 3416033 | 1575 |
2005 | 3452969 | 2037 |
2006 | 3511452 | 3125 |
2007 | 3123147 | 4622 |
2008 | 3200147 | 3889 |
2009 | 3694671 | 3378 |
2010 | 3849536 | 3859 |
2011 | 4154261 | 3259 |
2012 | 10676731 | 2855 |
2013 | 7200797 | 2506 |
2014 | 8453557 | 2200 |
ID:(9664, 0)
Estimación de las probabilidades
Descripción
Si se asume que el número de picadas es de una por día (
| $p_i=\displaystyle\frac{\gamma i}{(1-i)p_b v \Lambda}$ |
que
| $p_v=\displaystyle\frac{\mu v}{p_b i(1-v)}$ |
que
ID:(8213, 0)
Simulador Malaria
Php
El simulador para el caso de malaria permite experimentar con los distintos parámetros y observar como se desarrollan las poblaciones de humanos y mosquitos infectados:
ID:(9660, 0)